快速排序的優化
三種快速排序以及快速排序的優化:
一:快速排序的基本思想
| 快排使用分治的思想: | 通過一趟排序將待排序序列分割成兩部分,其中一部分記錄的關鍵字均比另一部分記錄的關鍵字小。之後分別對這兩部分記錄繼續進行排序,以達到整個序列有序的目的。 |
二:快速排序的三個步驟
| 1.選擇基準 | 在待排序列中,按照某種方式挑出一個元素,作為“基準”(pivot) |
| 2.分割操作 | 以該基準在序列中的位置,把序列分成兩個子序列,此時基準左邊的比基準小,基準右邊的都比基準大 |
| 3.遞迴操作 |
遞迴地對兩個序列進行快速排序,直到序列為空或者只有一個元素。 |
三:選擇基準的方式
對於分治演算法,當每次劃分時,演算法若能都劃分成兩個子序列時,那麼分治演算法效率會達到最大。也就是說,基準的選擇將會決定演算法的效率。選擇基準的方式決定了兩個分割後子序列的長度,進而對整個演算法的效率產生決定性的影響。
最理想的方法:選擇基準恰好能把待排序序列分成兩個等長的子序列。
下面我們將介紹3種選擇基準的方法:
方法(1):固定位置(基礎)
①思想:取序列的第一個或最後一個元素作為基準。基本快速排序
int SelectPivot(int arr[] , int low , int high) { return arr[low];//選擇序列的第一個元素作為基準。 //return arr[high]; } //注意:基本快排選取第一個或者最後一個元素作為基準。
②測試資料:
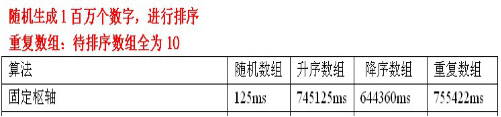
③測試資料分析:
如果輸入的序列是隨機的,處理時間可以接受。
但如果陣列已經有序了,此時的分割方法是一個非常不好的分割,因為每次分割只能使待排序序列減一,此時為最壞的情況,導致快速排序淪為氣泡排序。時間複雜度為O(n^2)。
因此,使用第一個元素作為樞紐元素是非常糟糕的,為了避免這種情況,就引入了下面兩個獲取基準的方法。
方法(2):隨機選取基準
①思想:隨機取帶排序元素中的元素作為基準。
/*隨機選擇樞軸的位置,區間在low和high之間*/ int SelectPivotRandom(int arr[],int low , int high) { srand((unsigned)time(NULL)); int pivotPos = rand()%(high - low) + low; //把樞軸位置的元素和low位置的元素互換,此時可以和普通的快排一樣呼叫換分函式 swap(arr[pivotPos],arr[low]); return arr[low]; }
②測試資料:
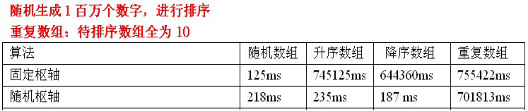
③:測試資料分析
這是一種相對安全的策略。由於樞軸的位置是隨機的,那麼產生的分割也不會總是出現劣質分割。
但是在整個陣列數字全相等時,認識最壞的情況,時間複雜度為O(n^2)。實際上:隨機化快排得到的理論上最壞的情況可能性僅僅為
1/(2^n)。所以隨機化快速排序可以對於絕大多數輸入資料達到O(nlogn)的期望時間複雜度。
一位前輩做出了一個精闢的總結:“隨機化快速排序可以滿足一個人一輩子的人品需求。”
方法(3):三數取中(median-of-three)(優化有序的資料)
引入的原因:雖然隨機選取樞軸時,減少出現不好分割的機率,但是最壞的情況下還是O(n^2),要緩解這種情況,就引入了三數取中的選取樞軸。
①:具體思想
對待排序序列中low,mid,high三個位置上資料進行排序,取他們中間的那個資料作為樞軸,並且用0下標元素儲存樞軸。
即:三數取中,並且0下標元素儲存樞軸。
/*函式作用:取待排序序列中low,mid,high三個位置上資料,選取他們中間的那個資料作為樞軸*/
int SelectPivotMedianOfThree( int arr[],int low,int high)
{
int mid = low + ((low + high)>>1);//計算陣列中間元素的下標。
if(arr[mid] > arr[high])//目標:arr[mid] <= arr[high]
{
swap(arr[mid] , arr[high]);
}
if(arr[low] > arr[high])
{
swap(arr[low] , arr[high]);
}
if(arr[mid] > arr[low])
{
swap(arr[mid] , arr[low]);
}
//此時,arr[mid]<=arr[low]<=arr[high]
return arr[low];
//low位置上儲存這三個位置中間的值,分割時可以直接使用low位置的元素作為樞軸,而不改用分割函數了
}
②:測試資料
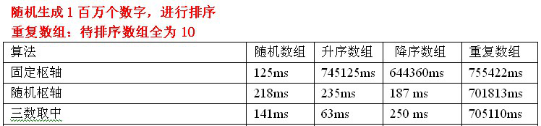
③:測試資料分析:使用三數取中選擇樞軸的優勢還是很明顯的,但是還是處理不了重複陣列
優化:
優化1:對於很小和部分有序的陣列。快排不如插入排序好。當待排序序列的長度分割到一定大小之後,繼續分割的效率比插入排序要差。此時可以使用插排而不是快排。
截至範圍:待排序序列長度N = 10.雖然在2 ~ 20之間任意截至範圍都有可能產生類似大的結果,這種做法也避免了一些有害的退化情形。摘自《資料結構與演算法分析》Mark Allen Weiness著。
if(high - low + 1 < 10)
{
insertSort(arr,low,high);
return ;
}
//else正常執行快排②:測試資料

③:測試資料分析
針對隨即陣列,使用三數取中選擇樞軸+插排,效率還是可以提高一點。
但是針對已排序陣列,是沒有作用的。因為待排序序列是已經有序的,那麼每次劃分只能使得待排序序列減一。此時插入排序是起不了任何作用的,所以這裡看不到任何的時間減少。
同時該方法對於重複陣列還是沒有任何的辦法。
優化2:再一次分割結束後,可以把與key相等的元素聚在一起。繼續下次分割時,不再用對於key相等元素分割。
①:具體的處理過程
| 第一步: | 再劃分過程中,把與key相等元素放入陣列的兩端。 |
| 第二步: | 劃分結束後,把與key相等的元素移到樞軸周圍。 |
舉例:
| 待排序序列:1 4 6 7 6 6 7 6 8 6 |
| 三數取中選取樞軸:下標為4 的數 6 |
| 轉化後待分割序列:6 4 6 7 1 6 7 6 8 6 樞軸key: 6 |
| 第一步:再劃分過程中,把與key相同的元素放入陣列的兩端 結果為: 6 4 1 6(樞軸) 7 8 7 6 6 6 。此時與6相等的元素全部放入兩端 |
| 第二步:劃分結束後,把與key相等的元素移到樞軸周圍。結果:1 4 6 6(樞軸) 6 6 6 7 8 7.此時與6相等的元素全移到樞軸周圍了。 |
| 之後,在1 4 和 7 8 7兩個子序列中進行快排。 |
void QSort(int arr[],int low,int high)
{
int first = low;
int lase = high;
int left = low;
int right = high;
int leftlen = 0;
int rightlen = 0;
if(high - low +1 < 10)
{
InsertSort(arr,low,high);
return;
}
//一次分割;
int key = SelectPivotMedianOfThree(arr,low,high);//使用三數取中選擇樞軸
while(low < high)
{
while(high < low && arr[high] >= key)
{
if(arr[high] == key)//處理相等元素
{
swap(arr[right],arr[high]);
right--;
rightlen++;
}
high--;
}
arr[low] = arr[high];
while(high > low && arr[low] <= key)
{
if(arr[low] == key)
{
swap(arr[left],arr[low]);
left++;
leftlen++;
}
low++
}
arr[high] = arr[low];
}
arr[low] = ley;
//一次排序結束
//把與樞軸key相同的元素移到樞軸最終位置周圍
int i = low - 1;
int j = first;
while(j < left && arr[i] != key)
{
swap(arr[i],arr[j]);
i--;
j++;
}
i = low +1;
j = last;
while(j > right && arr[i] != key)
{
swap(arr[i],arr[j]);
i++;
j--;
}
QSort(arr,first,low-1-leftlen);
QSort(arr,low + 1 + rightlen,last);
}
②:測試資料
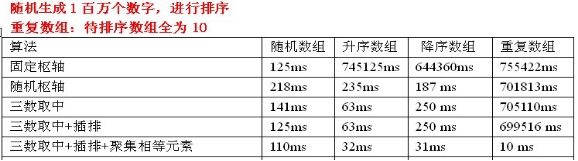
③:測試資料分析:三數取中選擇樞軸+插排+聚集相等元素的組合竟然效果好的 出奇。
原因:在陣列中,如果有相等的元素,那麼減少不少冗餘的劃分。這點再重複陣列中的體現特別明顯。(這裡的插排的作用還是不明顯)。
優化3:優化遞迴操作
①:思想:快排函式在函式末尾有兩次遞迴操作,我們可以對其使用尾遞迴優化。
②優點:如果待排序的序列劃分的極端不平衡,遞迴的深度將趨近於n,而棧的大小有限,每次遞迴呼叫都會耗費一定 的佔空間,函式引數越多,每次遞迴耗用的空間也就越多。優化後,可以縮減堆疊深度,由原來的O(n)縮減為O(log n)
void Qsrot(int arr[] , int low , int high)
{
int pivotPos = -1;
if(high - low + 1 < 10)
{
InsertSort(arr , low , high);
return;
}
while(low < high)
{
pivotPos = Partition(arr,low,high);
QSort(arr , low , pivot - 1);
low = pivot + 1;
}
}
注意:第一次遞迴後,low就沒用了;此時第二次遞迴可以使用迴圈代替。
②測試資料

③:測試分析:其實這種優化編譯器會自己優化,相比於不用該優化方法,時間幾乎沒少。
優化4:使用並行或多執行緒處理子程式(不詳細解釋)
所有的資料測試:

概括:這裡效率最好的快排組合 是:三數取中 + 快排 + 聚合相等元素。他和STL中的Sort函式的效率差不多。
