專案二:Kaggle房價預測(前篇)
概述
Kaggle房價預測比賽(高階技能篇)
notebook的背景是kaggle房價預測比賽高階迴歸技能篇
背景搬運如下:

這個notebook主要是通過資料探索和資料視覺化來實現。
我們把這個過程叫做EDA((Exploratory Data Analysis,探索性資料分析),它往往是比較枯燥乏味的工作。
但是你在理解、清洗和準備資料上花越多的時間,你的預測模型就會越加精準。
- 概述
- 匯入庫
- 匯入資料
- 變數識別
- 統計摘要描述
- 與目標變數的相關性
- 缺失值處理
- 找出含有缺失值的列
- 填充這些缺失值
- 資料視覺化
- 單變數分析
- 雙變數分析
匯入庫
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
% matplotlib inline
import seaborn as sns
sns.set(style="whitegrid", color_codes=True)
sns.set(font_scale=1)
import warnings
warnings.filterwarnings('ignore')
UsageError: Line magic function `%` not found.
匯入訓練資料集、測試資料
houses=pd.read_csv("./train.csv")
houses.head()
| Id | MSSubClass | MSZoning | LotFrontage | LotArea | Street | Alley | LotShape | LandContour | Utilities | ... | PoolArea | PoolQC | Fence | MiscFeature | MiscVal | MoSold | YrSold | SaleType | SaleCondition | SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 60 | RL | 65.0 | 8450 | Pave | NaN | Reg | Lvl | AllPub | ... | 0 | NaN | NaN | NaN | 0 | 2 | 2008 | WD | Normal | 208500 |
| 1 | 2 | 20 | RL | 80.0 | 9600 | Pave | NaN | Reg | Lvl | AllPub | ... | 0 | NaN | NaN | NaN | 0 | 5 | 2007 | WD | Normal | 181500 |
| 2 | 3 | 60 | RL | 68.0 | 11250 | Pave | NaN | IR1 | Lvl | AllPub | ... | 0 | NaN | NaN | NaN | 0 | 9 | 2008 | WD | Normal | 223500 |
| 3 | 4 | 70 | RL | 60.0 | 9550 | Pave | NaN | IR1 | Lvl | AllPub | ... | 0 | NaN | NaN | NaN | 0 | 2 | 2006 | WD | Abnorml | 140000 |
| 4 | 5 | 60 | RL | 84.0 | 14260 | Pave | NaN | IR1 | Lvl | AllPub | ... | 0 | NaN | NaN | NaN | 0 | 12 | 2008 | WD | Normal | 250000 |
5 rows × 81 columns
houses_test = pd.read_csv("./test.csv")
houses_test.head()
#注意:這裡沒有“銷售價格”這列,而“銷售價格”是我們的目標變數
| Id | MSSubClass | MSZoning | LotFrontage | LotArea | Street | Alley | LotShape | LandContour | Utilities | ... | ScreenPorch | PoolArea | PoolQC | Fence | MiscFeature | MiscVal | MoSold | YrSold | SaleType | SaleCondition | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1461 | 20 | RH | 80.0 | 11622 | Pave | NaN | Reg | Lvl | AllPub | ... | 120 | 0 | NaN | MnPrv | NaN | 0 | 6 | 2010 | WD | Normal |
| 1 | 1462 | 20 | RL | 81.0 | 14267 | Pave | NaN | IR1 | Lvl | AllPub | ... | 0 | 0 | NaN | NaN | Gar2 | 12500 | 6 | 2010 | WD | Normal |
| 2 | 1463 | 60 | RL | 74.0 | 13830 | Pave | NaN | IR1 | Lvl | AllPub | ... | 0 | 0 | NaN | MnPrv | NaN | 0 | 3 | 2010 | WD | Normal |
| 3 | 1464 | 60 | RL | 78.0 | 9978 | Pave | NaN | IR1 | Lvl | AllPub | ... | 0 | 0 | NaN | NaN | NaN | 0 | 6 | 2010 | WD | Normal |
| 4 | 1465 | 120 | RL | 43.0 | 5005 | Pave | NaN | IR1 | HLS | AllPub | ... | 144 | 0 | NaN | NaN | NaN | 0 | 1 | 2010 | WD | Normal |
5 rows × 80 columns
#模型命令:展示資料其特徵,包括行、樣本、例子的數量和列、特徵、預測的數量
#(行,列)
houses.shape
(1460, 81)
這裡一共有 1460個樣本 ,我們可以用這些樣本來訓練模型,共有 80個特徵 和 1個目標變數.
houses_test.shape
#缺少一列,因為目標變數並不在測試區間內
(1459, 80)
識別變數
#info命令,展示資料的相關資訊
#包含有每列的總和,空或非空,資料型別,記憶體佔用等
houses.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1460 entries, 0 to 1459
Data columns (total 81 columns):
Id 1460 non-null int64
MSSubClass 1460 non-null int64
MSZoning 1460 non-null object
LotFrontage 1201 non-null float64
LotArea 1460 non-null int64
Street 1460 non-null object
Alley 91 non-null object
LotShape 1460 non-null object
LandContour 1460 non-null object
Utilities 1460 non-null object
LotConfig 1460 non-null object
LandSlope 1460 non-null object
Neighborhood 1460 non-null object
Condition1 1460 non-null object
Condition2 1460 non-null object
BldgType 1460 non-null object
HouseStyle 1460 non-null object
OverallQual 1460 non-null int64
OverallCond 1460 non-null int64
YearBuilt 1460 non-null int64
YearRemodAdd 1460 non-null int64
RoofStyle 1460 non-null object
RoofMatl 1460 non-null object
Exterior1st 1460 non-null object
Exterior2nd 1460 non-null object
MasVnrType 1452 non-null object
MasVnrArea 1452 non-null float64
ExterQual 1460 non-null object
ExterCond 1460 non-null object
Foundation 1460 non-null object
BsmtQual 1423 non-null object
BsmtCond 1423 non-null object
BsmtExposure 1422 non-null object
BsmtFinType1 1423 non-null object
BsmtFinSF1 1460 non-null int64
BsmtFinType2 1422 non-null object
BsmtFinSF2 1460 non-null int64
BsmtUnfSF 1460 non-null int64
TotalBsmtSF 1460 non-null int64
Heating 1460 non-null object
HeatingQC 1460 non-null object
CentralAir 1460 non-null object
Electrical 1459 non-null object
1stFlrSF 1460 non-null int64
2ndFlrSF 1460 non-null int64
LowQualFinSF 1460 non-null int64
GrLivArea 1460 non-null int64
BsmtFullBath 1460 non-null int64
BsmtHalfBath 1460 non-null int64
FullBath 1460 non-null int64
HalfBath 1460 non-null int64
BedroomAbvGr 1460 non-null int64
KitchenAbvGr 1460 non-null int64
KitchenQual 1460 non-null object
TotRmsAbvGrd 1460 non-null int64
Functional 1460 non-null object
Fireplaces 1460 non-null int64
FireplaceQu 770 non-null object
GarageType 1379 non-null object
GarageYrBlt 1379 non-null float64
GarageFinish 1379 non-null object
GarageCars 1460 non-null int64
GarageArea 1460 non-null int64
GarageQual 1379 non-null object
GarageCond 1379 non-null object
PavedDrive 1460 non-null object
WoodDeckSF 1460 non-null int64
OpenPorchSF 1460 non-null int64
EnclosedPorch 1460 non-null int64
3SsnPorch 1460 non-null int64
ScreenPorch 1460 non-null int64
PoolArea 1460 non-null int64
PoolQC 7 non-null object
Fence 281 non-null object
MiscFeature 54 non-null object
MiscVal 1460 non-null int64
MoSold 1460 non-null int64
YrSold 1460 non-null int64
SaleType 1460 non-null object
SaleCondition 1460 non-null object
SalePrice 1460 non-null int64
dtypes: float64(3), int64(35), object(43)
memory usage: 924.0+ KB
#有多少列具有不同的資料型別?
houses.get_dtype_counts()
float64 3
int64 35
object 43
dtype: int64
##Describe命令,給出資料集中這些資料列的統計資訊
houses.describe()
| Id | MSSubClass | LotFrontage | LotArea | OverallQual | OverallCond | YearBuilt | YearRemodAdd | MasVnrArea | BsmtFinSF1 | ... | WoodDeckSF | OpenPorchSF | EnclosedPorch | 3SsnPorch | ScreenPorch | PoolArea | MiscVal | MoSold | YrSold | SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 1460.000000 | 1460.000000 | 1201.000000 | 1460.000000 | 1460.000000 | 1460.000000 | 1460.000000 | 1460.000000 | 1452.000000 | 1460.000000 | ... | 1460.000000 | 1460.000000 | 1460.000000 | 1460.000000 | 1460.000000 | 1460.000000 | 1460.000000 | 1460.000000 | 1460.000000 | 1460.000000 |
| mean | 730.500000 | 56.897260 | 70.049958 | 10516.828082 | 6.099315 | 5.575342 | 1971.267808 | 1984.865753 | 103.685262 | 443.639726 | ... | 94.244521 | 46.660274 | 21.954110 | 3.409589 | 15.060959 | 2.758904 | 43.489041 | 6.321918 | 2007.815753 | 180921.195890 |
| std | 421.610009 | 42.300571 | 24.284752 | 9981.264932 | 1.382997 | 1.112799 | 30.202904 | 20.645407 | 181.066207 | 456.098091 | ... | 125.338794 | 66.256028 | 61.119149 | 29.317331 | 55.757415 | 40.177307 | 496.123024 | 2.703626 | 1.328095 | 79442.502883 |
| min | 1.000000 | 20.000000 | 21.000000 | 1300.000000 | 1.000000 | 1.000000 | 1872.000000 | 1950.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 2006.000000 | 34900.000000 |
| 25% | 365.750000 | 20.000000 | 59.000000 | 7553.500000 | 5.000000 | 5.000000 | 1954.000000 | 1967.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 5.000000 | 2007.000000 | 129975.000000 |
| 50% | 730.500000 | 50.000000 | 69.000000 | 9478.500000 | 6.000000 | 5.000000 | 1973.000000 | 1994.000000 | 0.000000 | 383.500000 | ... | 0.000000 | 25.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 6.000000 | 2008.000000 | 163000.000000 |
| 75% | 1095.250000 | 70.000000 | 80.000000 | 11601.500000 | 7.000000 | 6.000000 | 2000.000000 | 2004.000000 | 166.000000 | 712.250000 | ... | 168.000000 | 68.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 8.000000 | 2009.000000 | 214000.000000 |
| max | 1460.000000 | 190.000000 | 313.000000 | 215245.000000 | 10.000000 | 9.000000 | 2010.000000 | 2010.000000 | 1600.000000 | 5644.000000 | ... | 857.000000 | 547.000000 | 552.000000 | 508.000000 | 480.000000 | 738.000000 | 15500.000000 | 12.000000 | 2010.000000 | 755000.000000 |
8 rows × 38 columns
資料相關性
corr=houses.corr()["SalePrice"]
# print(np.argsort(corr, axis=0))
corr[np.argsort(corr, axis=0)[::-1]] #np.argsort()表示返回其排序的索引
SalePrice 1.000000
OverallQual 0.790982
GrLivArea 0.708624
GarageCars 0.640409
GarageArea 0.623431
TotalBsmtSF 0.613581
1stFlrSF 0.605852
FullBath 0.560664
TotRmsAbvGrd 0.533723
YearBuilt 0.522897
YearRemodAdd 0.507101
GarageYrBlt 0.486362
MasVnrArea 0.477493
Fireplaces 0.466929
BsmtFinSF1 0.386420
LotFrontage 0.351799
WoodDeckSF 0.324413
2ndFlrSF 0.319334
OpenPorchSF 0.315856
HalfBath 0.284108
LotArea 0.263843
BsmtFullBath 0.227122
BsmtUnfSF 0.214479
BedroomAbvGr 0.168213
ScreenPorch 0.111447
PoolArea 0.092404
MoSold 0.046432
3SsnPorch 0.044584
BsmtFinSF2 -0.011378
BsmtHalfBath -0.016844
MiscVal -0.021190
Id -0.021917
LowQualFinSF -0.025606
YrSold -0.028923
OverallCond -0.077856
MSSubClass -0.084284
EnclosedPorch -0.128578
KitchenAbvGr -0.135907
Name: SalePrice, dtype: float64
OverallQual ,GrLivArea ,GarageCars,GarageArea ,TotalBsmtSF, 1stFlrSF ,FullBath,TotRmsAbvGrd,YearBuilt, YearRemodAdd 這些變數與SalePrice銷售價格的相關性大於0.5
EnclosedPorch and KitchenAbvGr這些變數與SalePrice銷售價格的相關性呈現輕度負相關
這些變數是有助於預測房價的重要特徵。
#繪製相關性圖表
num_feat=houses.columns[houses.dtypes!=object] #house.dtypes!=object表示輸出不是object的型別
num_feat=num_feat[1:-1] #去掉第0項:ID
labels = []
values = []
for col in num_feat:
labels.append(col)
values.append(np.corrcoef(houses[col].values, houses.SalePrice.values)[0,1])
#np.corrcoef()計算皮爾遜相關係數,具體解釋可以看https://blog.csdn.net/u012162613/article/details/42213883
ind = np.arange(len(labels))
width = 0.9
fig, ax = plt.subplots(figsize=(9,18))
#fig,ax = plt.subplots()的意思是,同時在subplots裡建立一個fig物件,建立一個axis物件
# 這樣就不用先plt.figure()
# 再plt.add_subplot()了
rects = ax.barh(ind, np.array(values), color='red') #ax.barh表示水平條狀圖
ax.set_yticks(ind+((width)/2.)) #設定y軸刻度寬度
ax.set_yticklabels(labels, rotation='horizontal') #設定y軸標籤
ax.set_xlabel("Correlation coefficient")
ax.set_title("Correlation Coefficients w.r.t Sale Price");

correlations=houses.corr()
# print(correlations)
attrs = correlations.iloc[:-1,:-1] #目標變數除外的所有列
threshold = 0.5
#unstack()表示降維dataframe,轉換為行列形式,預設level=-1
important_corrs = (attrs[abs(attrs) > threshold][attrs != 1.0]) \
.unstack().dropna().to_dict()
#將得到的資料進行重新排序,並生成相關性的dataframe
unique_important_corrs = pd.DataFrame(
list(set([(tuple(sorted(key)),important_corrs[key]) for key in important_corrs])),
columns=['Attribute Pair', 'Correlation'])
#以絕對值進行分類排序
unique_important_corrs = unique_important_corrs.iloc[
abs(unique_important_corrs['Correlation']).argsort()[::-1]]
unique_important_corrs
| Attribute Pair | Correlation | |
|---|---|---|
| 16 | (GarageArea, GarageCars) | 0.882475 |
| 17 | (GarageYrBlt, YearBuilt) | 0.825667 |
| 4 | (GrLivArea, TotRmsAbvGrd) | 0.825489 |
| 1 | (1stFlrSF, TotalBsmtSF) | 0.819530 |
| 26 | (2ndFlrSF, GrLivArea) | 0.687501 |
| 6 | (BedroomAbvGr, TotRmsAbvGrd) | 0.676620 |
| 2 | (BsmtFinSF1, BsmtFullBath) | 0.649212 |
| 25 | (GarageYrBlt, YearRemodAdd) | 0.642277 |
| 15 | (FullBath, GrLivArea) | 0.630012 |
| 14 | (2ndFlrSF, TotRmsAbvGrd) | 0.616423 |
| 20 | (2ndFlrSF, HalfBath) | 0.609707 |
| 23 | (GarageCars, OverallQual) | 0.600671 |
| 9 | (GrLivArea, OverallQual) | 0.593007 |
| 8 | (YearBuilt, YearRemodAdd) | 0.592855 |
| 10 | (GarageCars, GarageYrBlt) | 0.588920 |
| 7 | (OverallQual, YearBuilt) | 0.572323 |
| 12 | (1stFlrSF, GrLivArea) | 0.566024 |
| 5 | (GarageArea, GarageYrBlt) | 0.564567 |
| 21 | (GarageArea, OverallQual) | 0.562022 |
| 24 | (FullBath, TotRmsAbvGrd) | 0.554784 |
| 0 | (OverallQual, YearRemodAdd) | 0.550684 |
| 11 | (FullBath, OverallQual) | 0.550600 |
| 18 | (GarageYrBlt, OverallQual) | 0.547766 |
| 22 | (GarageCars, YearBuilt) | 0.537850 |
| 13 | (OverallQual, TotalBsmtSF) | 0.537808 |
| 27 | (BsmtFinSF1, TotalBsmtSF) | 0.522396 |
| 19 | (BedroomAbvGr, GrLivArea) | 0.521270 |
| 3 | (2ndFlrSF, BedroomAbvGr) | 0.502901 |
這顯示了多重共線性。
線上性迴歸模型中,多重共線性是指特徵與其他多個特徵相關。當你的模型包含有多個與目標變數相關的因素,而這些因素也相關影響時,即為多重共線性發生。
問題:
多重共線性會增加了這些係數的標準誤差。
這意味著,多重共線性會使一些本應該顯著的變數,變得沒有那麼顯著。
三種方式可避免這種情況:
- 完全刪除這些變數
- 通過新增或一些操作,增加新的特徵變數
- 通過PCA(Principal Component Analysis,主成分分析), 來減少特徵變數的多重共線性.
熱力圖
import seaborn as sns
corrMatrix=houses[["SalePrice","OverallQual","GrLivArea","GarageCars",
"GarageArea","GarageYrBlt","TotalBsmtSF","1stFlrSF","FullBath",
"TotRmsAbvGrd","YearBuilt","YearRemodAdd"]].corr()
sns.set(font_scale=1.10) #font_scale表示影象與字型大小比例
plt.figure(figsize=(10, 10))
sns.heatmap(corrMatrix, vmax=.8, linewidths=0.01,
square=True,annot=True,cmap='viridis',linecolor="white")
plt.title('Correlation between features');
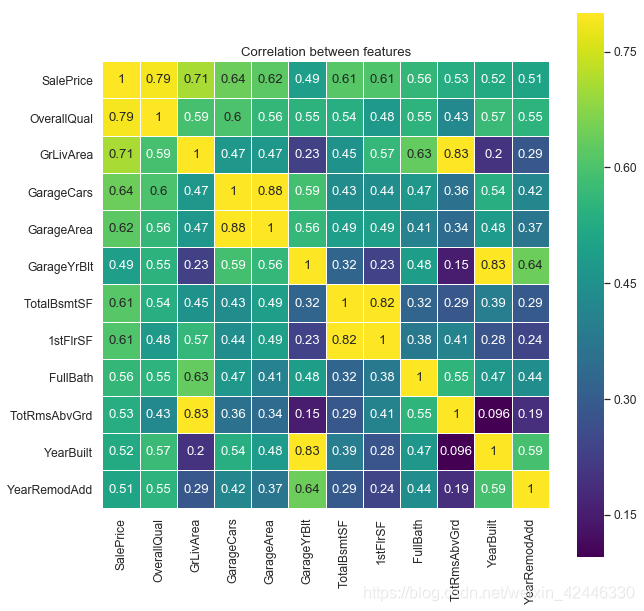
如我們所見,熱力圖中只有少量特徵變量表現出顯著的多重共線性。讓我們聚焦到對角線的黃色方塊和線框出的少量黃色區域。
SalePrice and OverallQual
GarageArea and GarageCars
TotalBsmtSF and 1stFlrSF
GrLiveArea and TotRmsAbvGrd
YearBulit and GarageYrBlt
在我們用這些變數進行預測之前,我們不得不新建一個源於這些變數的單特徵變數
關鍵特徵
houses[['OverallQual','SalePrice']].groupby(['OverallQual'],
as_index=False).mean().sort_values(by='OverallQual', ascending=False)
| OverallQual | SalePrice | |
|---|---|---|
| 9 | 10 | 438588.388889 |
| 8 | 9 | 367513.023256 |
| 7 | 8 | 274735.535714 |
| 6 | 7 | 207716.423197 |
| 5 | 6 | 161603.034759 |
| 4 | 5 | 133523.347607 |
| 3 | 4 | 108420.655172 |
| 2 | 3 | 87473.750000 |
| 1 | 2 | 51770.333333 |
| 0 | 1 | 50150.000000 |
houses[['GarageCars','SalePrice']].groupby(['GarageCars'],
as_index=False).mean().sort_values(by='GarageCars', ascending=False)
| GarageCars | SalePrice | |
|---|---|---|
| 4 | 4 | 192655.800000 |
| 3 | 3 | 309636.121547 |
| 2 | 2 | 183851.663835 |
| 1 | 1 | 128116.688347 |
| 0 | 0 | 103317.283951 |
houses[['Fireplaces','SalePrice']].groupby(['Fireplaces'],
as_index=False).mean().sort_values(by='Fireplaces', ascending=False)
| Fireplaces | SalePrice | |
|---|---|---|
| 3 | 3 | 252000.000000 |
| 2 | 2 | 240588.539130 |
| 1 | 1 | 211843.909231 |
| 0 | 0 | 141331.482609 |
目標變數的視覺化
單變數分析
1個單變數是如何分佈在一個數值區間上。
它的統計特徵是什麼。
它是正偏分佈,還是負偏分佈。
sns.distplot(houses['SalePrice'], color="r", kde=False)
plt.title("Distribution of Sale Price")
plt.ylabel("Number of Occurences")
plt.xlabel("Sale Price");
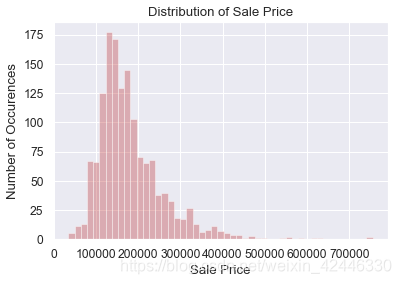
售價為正偏分佈,圖表顯示了一些峰度。
#偏度,表示在請求的軸上返回無偏傾斜
# 具體參考https:https://blog.csdn.net/colorknight/article/details/9531437
houses['SalePrice'].skew()
1.8828757597682129
#峰度,表示使用費雪的峰度定義在請求的軸上返回無偏峰度
houses['SalePrice'].kurt()
6.536281860064529
#刪除異常值
#np.percentile()沿著指定的軸計算資料的第q百分位數
upperlimit = np.percentile(houses.SalePrice.values, 99.5)
print(upperlimit)
houses['SalePrice'].loc[houses['SalePrice']>upperlimit] = upperlimit
plt.scatter(range(houses.shape[0]), houses["SalePrice"].values,color='orange')
plt.title("Distribution of Sale Price")
plt.xlabel("Number of Occurences")
plt.ylabel("Sale Price");
514508.61012787104
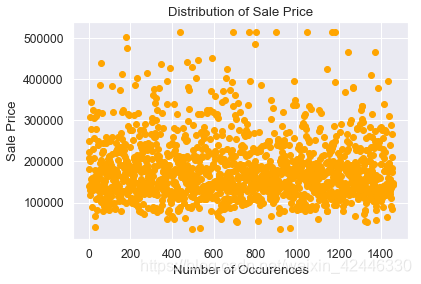
缺失值處理
====================
訓練資料集中的缺失值可能會對模型的預測或分類產生負面影響。
有一些機器學習演算法對資料缺失敏感,例如支援向量機 SVM(Support Vector Machine)
但是使用平均數/中位數/眾數來填充缺失值或使用其他預測模型來預測缺失值也不可能實現100%準確預測,比較可取的方式是你可以使用決策樹和隨機森林等模型來處理缺失值。
# 檢視是否有有缺失值的列
null_columns=houses.columns[houses.isnull().any()] #.any()表示是否所有元素為真
#得到null_columns為一個含空值的列的list
houses[null_columns].isnull().sum()
LotFrontage 259
Alley 1369
MasVnrType 8
MasVnrArea 8
BsmtQual 37
BsmtCond 37
BsmtExposure 38
BsmtFinType1 37
BsmtFinType2 38
Electrical 1
FireplaceQu 690
GarageType 81
GarageYrBlt 81
GarageFinish 81
GarageQual 81
GarageCond 81
PoolQC 1453
Fence 1179
MiscFeature 1406
dtype: int64
labels = []
values = []
for col in null_columns:
labels.append(col)
values.append(houses[col].isnull().sum())
ind = np.arange(len(labels))
width = 0.9
fig, ax = plt.subplots(figsize=(6,25))
rects = ax.barh(ind, np.array(values), color='violet')
ax.set_yticks(ind+((width)/2.))
ax.set_yticklabels(labels, rotation='horizontal')
ax.set_xlabel("Count of missing values")
ax.set_ylabel("Column Names")
ax.set_title("Variables with missing values");
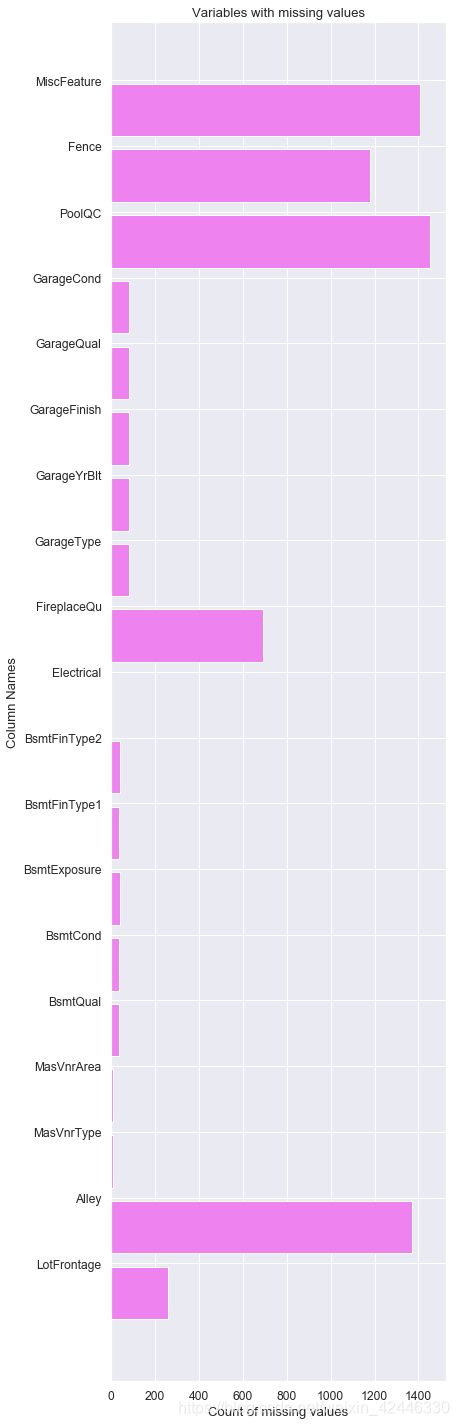
多變數分析
當我們去理解3個及以上變數之間的相互影響。
臨街距離
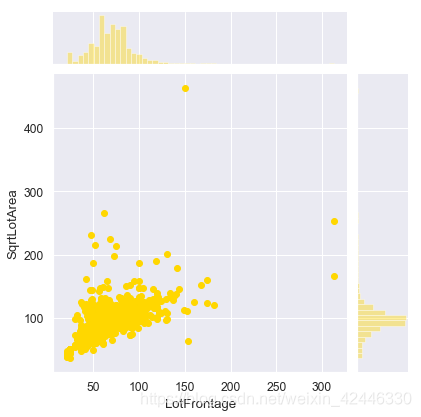
我們可以看看佔地面積和臨街距離之間是否存在某種關聯。
houses['LotFrontage'].corr(houses['LotArea'])
0.42609501877180816
這看起來不好,我們可以試試一些多項式表示式,如平方根
houses['SqrtLotArea']=np.sqrt(houses['LotArea'])
houses['LotFrontage'].corr(houses['SqrtLotArea'])
0.6020022167939364
0.60看起來不錯
sns.jointplot(houses['LotFrontage'],houses['SqrtLotArea'],color='gold');
filter = houses['LotFrontage'].isnull()
houses.LotFrontage[filter]=houses.SqrtLotArea[filter]
houses.LotFrontage
C:\ProgramData\Anaconda3\lib\site-packages\ipykernel_launcher.py:2: SettingWithCopyWarning:
A value is trying to be set on a copy of a slice from a DataFrame
See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy
0 65.000000
1 80.000000
2 68.000000
3 60.000000
4 84.000000
5 85.000000
6 75.000000
7 101.892100
8 51.000000
9 50.000000
10 70.000000
11 85.000000
12 113.877127
13 91.000000
14 104.498804
15 51.000000
16 106.023582
17 72.000000
18 66.000000
19 70.000000
20 101.000000
21 57.000000
22 75.000000
23 44.000000
24 90.807489
25 110.000000
26 60.000000
27 98.000000
28 47.000000
29 60.000000
...
1430 60.000000
1431 70.199715
1432 60.000000
1433 93.000000
1434 80.000000
1435 80.000000
1436 60.000000
1437 96.000000
1438 90.000000
1439 80.000000
1440 79.000000
1441 66.528190
1442 85.000000
1443 94.095696
1444 63.000000
1445 70.000000
1446 161.684879
1447 80.000000
1448 70.000000
1449 21.000000
1450 60.000000
1451 78.000000
1452 35.000000
1453 90.000000
1454 62.000000
1455 62.000000
1456 85.000000
1457 66.000000
1458 68.000000
1459 75.000000
Name: LotFrontage, Length: 1460, dtype: float64
砌體單板型別 and 砌體單板面積
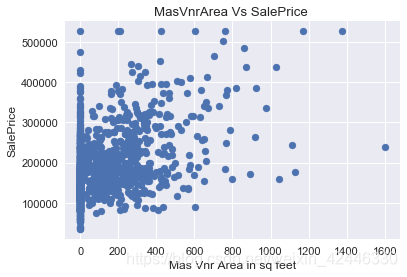
plt.scatter(houses["MasVnrArea"],houses["SalePrice"])
plt.title("MasVnrArea Vs SalePrice ")
plt.ylabel("SalePrice")
plt.xlabel("Mas Vnr Area in sq feet");
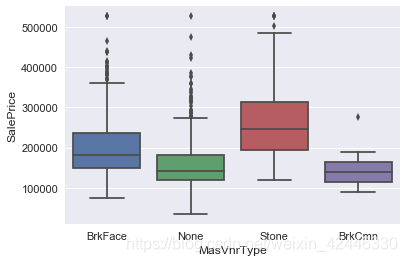
sns.boxplot("MasVnrType","SalePrice",data=houses);
houses["MasVnrType"] = houses["MasVnrType"].fillna('None')
houses["MasVnrArea"] = houses[<
