1.能被一些數整除 

(1)能被2整除的數，個位上的數都能被2整除
(2*)能被4整除的數，個位和十位所組成的兩位數能被4整除
(3*)能被8整除的數，百位、十位和個位所組成的三位數能被8整除
(4)能被5整除的數，末尾是0或5
(5*)能被25整除的數，十位和個位所組成的兩位數能被25整除
(6*)能被125整除的數，百位、十位和個位所組成的三位數能被125整除
(7)能被3整除的數，各個數位上的數字之和能被3整除
(8*)能被9整除的數，各個數位上的數字和能被 9 整除
(9)如果一個數既能被 2 整除又能被 3 整除，那麼這個數能被 6 整除
(10)如果一個數既能被 2 整除又能被 5 整除，那麼這個數能被 10 整除（即個位為0）
(11*)能被 11 整除的數，奇數位（從左往右數）上的數字和與偶數位上的數字和的差（大數減小數）能被 11 整除

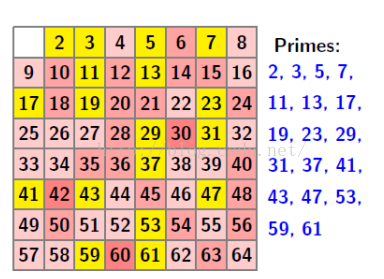
2.素數的篩法（不是很大的資料）

Primes 中存放的都是素數，就是把素數的倍數都標記成素數。

#include<iostream>
#include<cstring>
using namespace std;
#define Max 1005 
int prime[Max];
void IsPrime(){
     memset(prime,1,sizeof(prime));
     prime[0]=0;
     prime[1]=0;
     for(int i=2;i*i<Max;i++){
     	if(!prime[i])
     	    continue;
     	for(int j=i*2;j<Max;j+=i)
            prime[j]=0;
	 }
} 
int main(){
	IsPrime();
	for(int i=1;i<=Max;i++) 
	    if(prime[i]!=0)
	       cout<<i<<endl;
} 
 

3.區間素數

給定N,M, N和M都很大，但是M-N卻很小，讓我們求出M-N中的素數，可以先用線性篩打表，然後輸出N到M中的素數 

4.判定素數

肯定有那個O(sqrt N)的方法了

5.唯一定理

概念：任意一個大於0的正整數都能被表示成若干個素數的乘積且表示方法是唯一的

任意一個合數都可以寫成如下形式：

a的因子數= (a1+1)×(a2+1)×....×(ar+1)