1099 Build A Binary Search Tree （30 分）

A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:
The left subtree of a node contains only nodes with keys less than the node’s key.
The right subtree of a node contains only nodes with keys greater than or equal to the node’s key.
Both the left and right subtrees must also be binary search trees.
Given the structure of a binary tree and a sequence of distinct integer keys, there is only one way to fill these keys into the tree so that the resulting tree satisfies the definition of a BST. You are supposed to output the level order traversal sequence of that tree. The sample is illustrated by Figure 1 and 2.

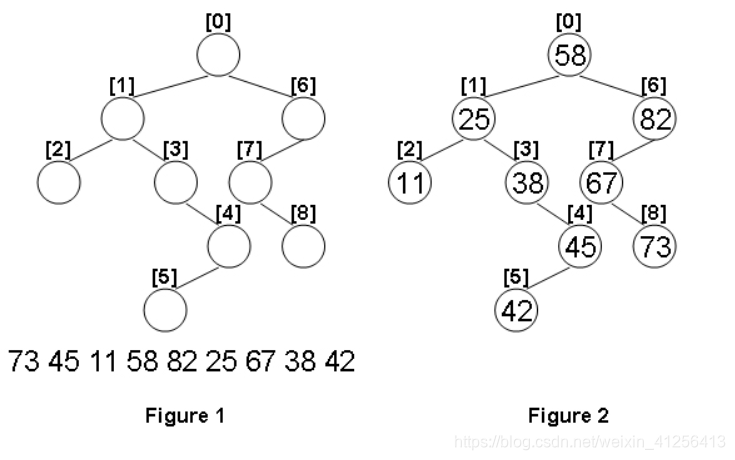
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (≤100) which is the total number of nodes in the tree. The next N lines each contains the left and the right children of a node in the format left_index right_index, provided that the nodes are numbered from 0 to N−1, and 0 is always the root. If one child is missing, then −1 will represent the NULL child pointer. Finally N distinct integer keys are given in the last line.

Output Specification:
For each test case, print in one line the level order traversal sequence of that tree. All the numbers must be separated by a space, with no extra space at the end of the line.

Sample Input:

9
1 6
2 3
-1 -1
-1 4
5 -1
-1 -1
7 -1
-1 8
-1 -1
73 45 11 58 82 25 67 38 42

Sample Output:

58 25 82 11 38 67 45 73 42

解析

#include<algorithm>
#include<functional>
#include<cstdio>
#include<iostream>
#include<queue>
#include<string>
#include<cmath>
using namespace std;
const int MAXN = 101;
vector<int> input,layer;
int num = 0;
struct node {
	int value;
	int left, right;
	node(int v = 0):value(v),left(-1),right(-1){}
}Node[MAXN];
void inorder(int root) {
	if (root == -1)
		return;
	inorder(Node[root].left);
	Node[root].value = input[num++];
	inorder(Node[root].right);
}
void Layerorder(){
	queue<int> Q;
	Q.push(0);
	while (!Q.empty()) {
		int temp = Q.front();
		Q.pop();
		layer.push_back(Node[temp].value);
		if (Node[temp].left != -1) Q.push(Node[temp].left);
		if (Node[temp].right != -1) Q.push(Node[temp].right);
	}
}
int main()
{
	int N,son1,son2;
	scanf("%d", &N);
	for (int i = 0; i < N; i++) {
		scanf("%d %d", &son1, &son2);
		Node[i].left = son1;
		Node[i].right = son2;
	}
	input.resize(N, 0);
	for (int i = 0; i < N; i++)
		scanf("%d", &input[i]);
	sort(input.begin(), input.end());
	inorder(0);
	Layerorder();
	for (int i = 0; i < N; i++)
		printf("%d%c", layer[i], i == N - 1 ? '\n' : ' ');
}