K-臨近演算法原理

簡單地說，K-近鄰演算法採用測量不同特徵值之間的距離方法進行分類。
存在一個樣本資料集合，也稱作訓練樣本集，並且樣本集中每個資料都存在標籤，即我們知道樣本集中每一資料 與所屬分類的對應關係。
輸入沒有標籤的新資料後，將新資料的每個特徵與樣本集中資料對應的 特徵進行比較，常用的是計算歐幾里得距離，然後演算法提取樣本集中特徵最相似資料（最近鄰）的分類標籤。
一般來說，我們 只選擇樣本資料集中前K個最相似的資料，這就是K-近鄰演算法中K的出處,通常K是不大於20的整數。 最後 ，選擇K個最相似資料中出現次數最多的分類，作為新資料的分類。

例項:選取鳶尾花資料進行分類

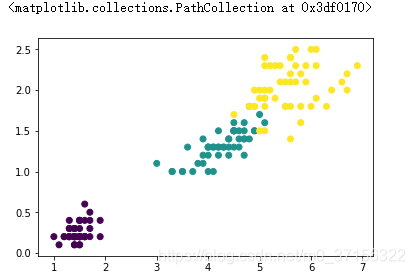
# load_iris是機器學習庫提供給我們研究演算法的資料
from sklearn.datasets import load_iris
iris = load_iris()
data = iris.data # 150個花的特徵資料
target = iris.target # 每個資料對應的分類結果
target_names = iris.target_names # 每個結果對應的名字
feature_names = iris.feature_names # 所有的特徵

features = DataFrame(data=data,columns = feature_names)

# 獲取訓練集和測試集，為了能夠在圖上顯示，只選擇兩個特徵進行

features.iloc[:,0].std()
#0.828066127977863

features.iloc[:,2].std()
#1.7652982332594662

features.iloc[:,1].std()
#0.4358662849366982

features.iloc[:,3].std()
#0.7622376689603465

# 選區標準差較大的兩個作為訓練資料
# samples(訓練集、測試集)
X_train = features.iloc[:130,2:4]
y_train = target[:130]

# 測試集(驗證訓練模型的準確度)
X_test = features.iloc[130:,2:4]
y_test = target[130:]

# 繪製圖形
import matplotlib.pyplot as plt
%matplotlib inline
samples = features.iloc[:,2:4]

# 展示真實資料的分類情況
plt.scatter(samples.iloc[:,0],samples.iloc[:,1],c=target)
 

# 定義KNN分類器,訓練資料，生成預測結果。
knnclf = KNeighborsClassifier(n_neighbors=5)
knnclf.fit(X_train,y_train)
y_ = knnclf.predict(X_test)

# 獲取所有預測點（滿螢幕的點），將滿螢幕的點最為預測資料
xmin,xmax = samples.iloc[:,0].min(),samples.iloc[:,0].max()
ymin,ymax = samples.iloc[:,1].min(),samples.iloc[:,1].max()

x = np.linspace(xmin,xmax,100)
y = np.linspace(ymin,ymax,100)

xx,yy = np.meshgrid(x,y)

X_test = np.c_[xx.ravel(),yy.ravel()]
y_ = knnclf.predict(X_test)
# 顯示資料
from matplotlib.colors import ListedColormap

cmap = ListedColormap(['#aa00ff','#00aaff','#ffaa00'])

# 展示預測資料的分類情況
plt.scatter(X_test[:,0],X_test[:,1],c=y_,cmap=cmap)
# 展示真實資料的分類情況
plt.scatter(samples.iloc[:,0],samples.iloc[:,1],c=target)
 

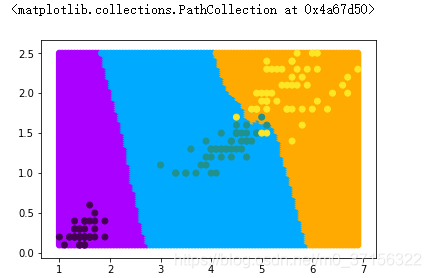
KNN演算法還可用於迴歸分析

第一步：生成模型，並訓練資料
第二步：使用模型，預測資料
大概思路，使用周圍幾個點（根據n_neighbors的取值）座標的平均值作為線上的點

小結

• 優點：精度高、對異常值不敏感、無資料輸入假定。
• 缺點：時間複雜度高、空間複雜度高。
• 適用資料範圍：數值型和標稱型。