k-最近鄰演算法是基於例項的學習方法中最基本的，先介紹基於例項學習的相關概念。

基於例項的學習

1. 已知一系列的訓練樣例，很多學習方法為目標函式建立起明確的一般化描述；但與此不同，基於例項的學習方法只是簡單地把訓練樣例儲存起來。
   從這些例項中泛化的工作被推遲到必須分類新的例項時。每當學習器遇到一個新的查詢例項，它分析這個新例項與以前儲存的例項的關係，並據此把一個目標函式值賦給新例項。
2. 基於例項的方法可以為不同的待分類查詢例項建立不同的目標函式逼近。事實上，很多技術只建立目標函式的區域性逼近，將其應用於與新查詢例項鄰近的例項，而從 不建立在整個例項空間上都表現良好的逼近。當目標函式很複雜，但它可用不太複雜的區域性逼近描述時，這樣做有顯著的優勢。
3. 基於例項方法的不足
   • 分類新例項的開銷可能很大。這是因為幾乎所有的計算都發生在分類時，而不是在第一次遇到訓練樣例時。所以，如何有效地索引訓練樣例，以減少查詢時所需計算是一個重要的實踐問題。
   • 當從儲存器中檢索相似的訓練樣例時，它們一般考慮例項的所有屬性。如果目標概念僅依賴於很多屬性中的幾個時，那麼真正最“相似”的例項之間很可能相距甚遠。

k-最近鄰法

演算法概述

K最近鄰(K-Nearest Neighbor,KNN)演算法，是著名的模式識別統計學方法，在機器學習分類演算法中佔有相當大的地位。它是一個理論上比較成熟的方法。既是最簡單的機器學習演算法之一，也是基於例項的學習方法中最基本的，又是最好的文字分類演算法之一。

基本思想

如果一個例項在特徵空間中的K個最相似（即特徵空間中最近鄰）的例項中的大多數屬於某一個類別，則該例項也屬於這個類別。所選擇的鄰居都是已經正確分類的例項。
該演算法假定所有的例項對應於N維歐式空間Ân中的點。通過計算一個點與其他所有點之間的距離，取出與該點最近的K個點，然後統計這K個點裡面所屬分類比例最大的，則這個點屬於該分類。
該演算法涉及3個主要因素：例項集、距離或相似的衡量、k的大小。
一個例項的最近鄰是根據標準歐氏距離定義的。更精確地講，把任意的例項x表示為下面的特徵向量：

<a1(x)，a2(x)，...，an(x)>

其中ar(x)表示例項x的第r個屬性值。那麼兩個例項xi和xj間的距離定義為d

d(xi,xj)=∑r=1n(ar(xi)−ar(xj))2−−−−−−−−−−−−−−−−−√

有關KNN演算法的幾點說明：

1. 在最近鄰學習中，目標函式值可以為離散值也可以為實值。
2. 我們先考慮學習以下形式的離散目標函式。其中V是有限集合{v1,...,vs}。下表給出了逼近離散目標函式的k-近鄰演算法。
3. 正如下表中所指出的，這個演算法的返回值f′(xq)為對f(xq)的估計，它就是距離xq最近的k個訓練樣例中最普遍的f值。
4. 如果我們選擇k=1，那麼“1-近鄰演算法”就把f(xi)賦給(xq)，其中xi是最靠近xq的訓練例項。對於較大的k值，這個演算法返回前k個最靠近的訓練例項中最普遍的f值。

逼近離散值函式f:Ân−V的k-近鄰演算法
訓練演算法：
對於每個訓練樣例<x,f(x)>，把這個樣例加入列表training_examples
分類演算法：
給定一個要分類的查詢例項xq
在training_examples中選出最靠近xq的k個例項，並用x1,....,xk表示
返回
其中如果a=b那麼d(a,b)=1，否則d(a,b)=0

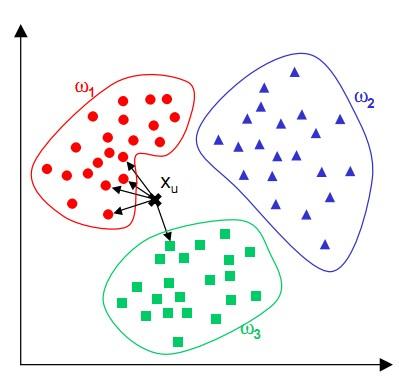
簡單來說，KNN可以看成：有那麼一堆你已經知道分類的資料，然後當一個新資料進入的時候，就開始跟訓練資料裡的每個點求距離，然後挑離這個訓練資料最近的K個點看看這幾個點屬於什麼型別，然後用少數服從多數的原則，給新資料歸類。

KNN演算法的決策過程

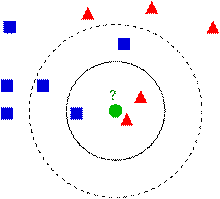
下圖中有兩種型別的樣本資料，一類是藍色的正方形，另一類是紅色的三角形，中間那個綠色的圓形是待分類資料：

如果K=3，那麼離綠色點最近的有2個紅色的三角形和1個藍色的正方形，這三個點進行投票，於是綠色的待分類點就屬於紅色的三角形。而如果K=5，那麼離綠色點最近的有2個紅色的三角形和3個藍色的正方形，這五個點進行投票，於是綠色的待分類點就屬於藍色的正方形。
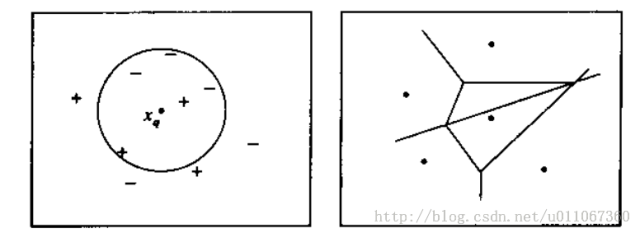
下圖則圖解了一種簡單情況下的k-最近鄰演算法，在這裡例項是二維空間中的點，目標函式具有布林值。正反訓練樣例用“+”和“-”分別表示。圖中也畫出了一個查詢點xq。注意在這幅圖中，1-近鄰演算法把xq分類為正例，然而5-近鄰演算法把xq分類為反例。

圖解說明：左圖畫出了一系列的正反訓練樣例和一個要分類的查詢例項xq。1-近鄰演算法把xq分類為正例，然而5-近鄰演算法把xq分類為反例。
右圖是對於一個典型的訓練樣例集合1-近鄰演算法導致的決策面。圍繞每個訓練樣例的凸多邊形表示最靠近這個點的例項空間（即這個空間中的例項會被1-近鄰演算法賦予該訓練樣例所屬的分類）。
對前面的k-近鄰演算法作簡單的修改後，它就可被用於逼近連續值的目標函式。為了實現這一點，我們讓演算法計算k個最接近樣例的平均值，而不是計算其中的最普遍的值。更精確地講，為了逼近一個實值目標函式f:Rn⟶R，我們只要把演算法中的公式替換為：

f(xq)⟵∑ki=1f(xi)k

針對傳統KNN演算法的改進

1. 快速KNN演算法。參考FKNN論述文獻（實際應用中結合lucene）
2. 加權歐氏距離公式。在傳統的歐氏距離中,各特徵的權重相同,也就是認定各個特徵對於分類的貢獻是相同的,顯然這是不符合實際情況的。同等的權重使得特徵向量之間相似度計算不夠準確, 進而影響分類精度。加權歐氏距離公式,特徵權重通過靈敏度方法獲得（根據業務需求調整，例如關鍵字加權、詞性加權等）

距離加權最近鄰演算法

對k-最近鄰演算法的一個顯而易見的改進是對k個近鄰的貢獻加權，根據它們相對查詢點xq的距離，將較大的權值賦給較近的近鄰。
例如，在上表逼近離散目標函式的演算法中，我們可以根據每個近鄰與xq的距離平方的倒數加權這個近鄰的“選舉權”。
方法是通過用下式取代上表演算法中的公式來實現：

f(xq)⟵argmaxv∈V∑i=1kwiδ(v,f(xi))

其中

wi≡1d(xq,xi)2

為了處理查詢點xq恰好匹配某個訓練樣例xi，從而導致分母為0的情況，我們令這種情況下的f′(xq)等於f(xi)。如果有多個這樣的訓練樣例，我們使用它們中佔多數的分類。
我們也可以用類似的方式對實值目標函式進行距離加權，只要用下式替換上表的公式：

 

f(xq)⟵∑ki=1wif(xi)∑ki=1wi

其中wi的定義與之前公式中相同。
注意這個公式中的分母是一個常量，它將不同權值的貢獻歸一化（例如，它保證如果對所有的訓練樣例xi，f(xi)=c，那麼(xq)←c)。
注意以上k-近鄰演算法的所有變體都只考慮k個近鄰以分類查詢點。如果使用按距離加權，那麼允許所有的訓練樣例影響xq的分類事實上沒有壞處，因為非常遠的例項對(xq)的影響很小。考慮所有樣例的惟一不足是會使分類執行得更慢。如果分類一個新的查詢例項時考慮所有的訓練樣例，我們稱此為全域性（global）法。如果僅考慮最靠近的訓練樣例，我們稱此為區域性（local）法。
四、KNN的優缺點
（1）優點
①簡單，易於理解，易於實現，無需引數估計，無需訓練;
②精度高，對異常值不敏感（個別噪音資料對結果的影響不是很大）;
③適合對稀有事件進行分類;
④特別適合於多分類問題(multi-modal,物件具有多個類別標籤)，KNN要比SVM表現要好.
（2）缺點
①對測試樣本分類時的計算量大，空間開銷大，因為對每一個待分類的文字都要計算它到全體已知樣本的距離，才能求得它的K個最近鄰點。目前常用的解決方法是事先對已知樣本點進行剪輯，事先去除對分類作用不大的樣本;
②可解釋性差，無法給出決策樹那樣的規則;
③最大的缺點是當樣本不平衡時，如一個類的樣本容量很大，而其他類樣本容量很小時，有可能導致當輸入一個新樣本時，該樣本的K個鄰居中大容量類的樣本佔多數。該演算法只計算“最近的”鄰居樣本，某一類的樣本數量很大，那麼或者這類樣本並不接近目標樣本，或者這類樣本很靠近目標樣本。無論怎樣，數量並不能影響執行結果。可以採用權值的方法（和該樣本距離小的鄰居權值大）來改進;
④消極學習方法。

五、對k-近鄰演算法的說明
按距離加權的k-近鄰演算法是一種非常有效的歸納推理方法。它對訓練資料中的噪聲有很好的魯棒性，而且當給定足夠大的訓練集合時它也非常有效。注意通過取k個近鄰的加權平均，可以消除孤立的噪聲樣例的影響。
問題一：近鄰間的距離會被大量的不相關屬性所支配。
應用k-近鄰演算法的一個實踐問題是，例項間的距離是根據例項的所有屬性（也就是包含例項的歐氏空間的所有座標軸）計算的。這與那些只選擇全部例項屬性的一個子集的方法不同，例如決策樹學習系統。
比如這樣一個問題：每個例項由20個屬性描述，但在這些屬性中僅有2個與它的分類是有關。在這種情況下，這兩個相關屬性的值一致的例項可能在這個20維的例項空間中相距很遠。結果，依賴這20個屬性的相似性度量會誤導k-近鄰演算法的分類。近鄰間的距離會被大量的不相關屬性所支配。這種由於存在很多不相關屬性所導致的難題，有時被稱為維度災難（curse of dimensionality）。最近鄰方法對這個問題特別敏感。
解決方法：當計算兩個例項間的距離時對每個屬性加權。
這相當於按比例縮放歐氏空間中的座標軸，縮短對應於不太相關屬性的座標軸，拉長對應於更相關的屬性的座標軸。每個座標軸應伸展的數量可以通過交叉驗證的方法自動決定。
問題二：應用k-近鄰演算法的另外一個實踐問題是如何建立高效的索引。因為這個演算法推遲所有的處理，直到接收到一個新的查詢，所以處理每個新查詢可能需要大量的計算。
解決方法：目前已經開發了很多方法用來對儲存的訓練樣例進行索引，以便在增加一定儲存開銷情況下更高效地確定最近鄰。一種索引方法是kd-tree（Bentley 1975；Friedman et al. 1977），它把例項儲存在樹的葉結點內，鄰近的例項儲存在同一個或附近的結點內。通過測試新查詢xq的選定屬性，樹的內部結點把查詢xq排列到相關的葉結點。

Python實現KNN演算法

這裡實現一個手寫識別演算法，這裡只簡單識別0~9數字。
輸入：每個手寫數字已經事先處理成32*32的二進位制文字，儲存為txt檔案。每個數字大約有200個樣本。每個樣本保持在一個txt檔案中。手寫體影象本身的大小是32x32的二值圖，轉換到txt檔案儲存後，內容也是32x32個數字，如下圖所示。目錄trainingDigits存放的是大約2000個訓練資料，testDigits存放大約900個測試資料。

• 函式img2vector：用來生成將每個樣本的txt檔案轉換為對應的一個向量

# convert image to vector  
def  img2vector(filename):  
    rows = 32  
    cols = 32  
    imgVector = zeros((1, rows * cols))   
    fileIn = open(filename)  
    for row in xrange(rows):  
        lineStr = fileIn.readline()  
        for col in xrange(cols):  
            imgVector[0, row * 32 + col] = int(lineStr[col])  

    return imgVector

• 函式loadDDataSet：載入整個資料庫

# load dataSet  
def loadDataSet():  
    ## step 1: Getting training set  
    print "---Getting training set..."  
    dataSetDir = './'
    trainingFileList = os.listdir(dataSetDir + 'trainingDigits') # load the training set  
    numSamples = len(trainingFileList)  

    train_x = zeros((numSamples, 1024))  
    train_y = []  
    for i in xrange(numSamples):  
        filename = trainingFileList[i]  

        # get train_x  
        train_x[i, :] = img2vector(dataSetDir + 'trainingDigits/%s' % filename)   

        # get label from file name such as "1_18.txt"  
        label = int(filename.split('_')[0]) # return 1  
        train_y.append(label)  

    ## step 2: Getting testing set  
    print "---Getting testing set..."  
    testingFileList = os.listdir(dataSetDir + 'testDigits') # load the testing set  
    numSamples = len(testingFileList)  
    test_x = zeros((numSamples, 1024))  
    test_y = []  
    for i in xrange(numSamples):  
        filename = testingFileList[i]  

        # get train_x  
        test_x[i, :] = img2vector(dataSetDir + 'testDigits/%s' % filename)   

        # get label from file name such as "1_18.txt"  
        label = int(filename.split('_')[0]) # return 1  
        test_y.append(label)  

    return train_x, train_y, test_x, test_y 

• 函式kNNClassify:實現kNN分類演算法

# classify using kNN  
def kNNClassify(newInput, dataSet, labels, k):  
    numSamples = dataSet.shape[0] # shape[0] stands for the num of row  

    ## step 1: calculate Euclidean distance  
    # tile(A, reps): Construct an array by repeating A reps times  
    # the following copy numSamples rows for dataSet  
    diff = tile(newInput, (numSamples, 1)) - dataSet # Subtract element-wise
    squaredDiff = diff ** 2 # squared for the subtract  
    squaredDist = sum(squaredDiff, axis = 1) # sum is performed by row  
    distance = squaredDist ** 0.5  

    ## step 2: sort the distance  
    # argsort() returns the indices that would sort an array in a ascending order  
    sortedDistIndices = argsort(distance)  

    classCount = {} # define a dictionary (can be append element)  
    for i in xrange(k):  
        ## step 3: choose the min k distance  
        voteLabel = labels[sortedDistIndices[i]]  

        ## step 4: count the times labels occur  
        # when the key voteLabel is not in dictionary classCount, get()  
        # will return 0  
        classCount[voteLabel] = classCount.get(voteLabel, 0) + 1  

    ## step 5: the max voted class will return  
    maxCount = 0  
    for key, value in classCount.items():  
        if value > maxCount:  
            maxCount = value  
            maxIndex = key  

    return maxIndex 

• 函式testHandWritingClass:測試函式

# test hand writing class  
def testHandWritingClass():  
    ## step 1: load data  
    print "step 1: load data..."  
    train_x, train_y, test_x, test_y = loadDataSet()  

    ## step 2: training...  
    print "step 2: training..."  
    pass  

    ## step 3: testing  
    print "step 3: testing..."  
    numTestSamples = test_x.shape[0]  
    matchCount = 0  
    for i in xrange(numTestSamples):  
        predict = kNNClassify(test_x[i], train_x, train_y, 3)
        if predict == test_y[i]:  
            matchCount += 1  
    accuracy = float(matchCount) / numTestSamples  

    ## step 4: show the result  
    print "step 4: show the result..."  
    print 'The classify accuracy is: %.2f%%' % (accuracy * 100) 

相似性度量

相似性一般用空間內兩個點的距離來度量。距離越大，表示兩個越不相似。
作為相似性度量的距離函式一般滿足下列性質:

• d(X,Y)=d(Y,X);
• d(X,Y)≦d(X,Z)+d(Z,Y);
• d(X,Y)≧0;
• d(X,Y)=0,當且僅當X=Y;

這裡，X,Y和Z是對應特徵空間中的三個點。
假設X,Y分別是N維特徵空間中的一個點，其中X=(x1,x2,...,xn)T,Y=(y1,y2,...,yn)T,d(X,Y)表示相應的距離函式，它給出了X和Y之間的距離測度。

距離的選擇有很多種，常用的距離函式如下：
1. 明考斯基(Minkowsky)距離

d(X,Y)=[∑i=1n∣xi−yi∣λ]1λ,λ一般取整數值，不同的λ取值對應於不同的距離

1. 曼哈頓(Manhattan)距離

   d(X,Y)=∑i=1n∣xi−yi∣，該距離是Minkowsky距離在λ=1時的一個特例

2. Cityblock距離

   d(X,Y)=∑i=1nwi∣xi−yi∣，該距離是Manhattan距離的加權修正，其中wi,i=1,2,...,n是權重因子

3. 歐幾里德(Euclidean)距離（歐式距離）

   d(X,Y)=[∑i=1n∣xi−yi∣2]12=(X−Y)(X−Y)T−−−−−−−−−−−−−−√，是Minkowsky距離在λ=2時的特例

4. Canberra距離

   d(X,Y)=∑i=1nxi−yixi+yi

(6)Mahalanobis距離(馬式距離)

d(X,M)=(X−M)TΣ−1(X−M)−−−−−−−−−−−−−−−−−−√

d(X,M)給出了特徵空間中的點X和M之間的一種距離測度，其中M為某一個模式類別的均值向量，∑為相應模式類別的協方差矩陣。
該距離測度考慮了以M為代表的模式類別在特徵空間中的總體分佈,能夠緩解由於屬性的線性組合帶來的距離失真。易見，到M的馬式距離為常數的點組成特徵空間中的一個超橢球面。

1. 切比雪夫(Chebyshev)距離

   d(X,Y)=maxi(∣xi−yi∣)

    

   L∞=limk→∞(∑i=1k∣xi−yi∣k)1k

   
   切比雪夫距離或是L∞度量是向量空間中的一種度量，二個點之間的距離定義為其各座標數值差的最大值。在二維空間中。以(x1,y1)和(x2,y2)二點為例，其切比雪夫距離為

   d=max(∣x2−x1∣,∣y2−y1∣)

   切比雪夫距離或是L∞度量是向量空間中的一種度量，二個點之間的距離定義為其各座標數值差的最大值。在二維空間中。以(x1,y1)和(x2,y2)二點為例，其切比雪夫距離為

   d=max(|x2−x1|,|y2−y1|)

2. 平均距離

   daverage=[1n∑i=1n(xi−yi)2]12

消極學習與積極學習

1. 積極學習(Eager Learning)
   這種學習方式是指在進行某種判斷（例如，確定一個點的分類或者回歸中確定某個點對應的函式值）之前，先利用訓練資料進行訓練得到一個目標函式，待需要時就只利用訓練好的函式進行決策，顯然這是一種一勞永逸的方法，SVM就屬於這種學習方式。
2. 消極學習(Lazy Learning)
   這種學習方式指不是根據樣本建立一般化的目標函式並確定其引數，而是簡單地把訓練樣本儲存起來，直到需要分類新的例項時才分析其與所儲存樣例的關係，據此確定新例項的目標函式值。也就是說這種學習方式只有到了需要決策時才會利用已有資料進行決策，而在這之前不會經歷 Eager Learning所擁有的訓練過程。KNN就屬於這種學習方式。

3. 比較

   • Eager Learning考慮到了所有訓練樣本，說明它是一個全域性的近似，雖然它需要耗費訓練時間，但它的決策時間基本為0.
   • Lazy Learning在決策時雖然需要計算所有樣本與查詢點的距離，但是在真正做決策時卻只用了局部的幾個訓練資料，所以它是一個區域性的近似，然而雖然不需要訓練，它的複雜度還是需要 O(n),n 是訓練樣本的個數。由於每次決策都需要與每一個訓練樣本求距離，這引出了Lazy Learning的缺點：(1)需要的儲存空間比較大 (2)決策過程比較慢。

4. 典型演算法

   • 積極學習方法:SVM;Find-S演算法;候選消除演算法;決策樹;人工神經網路;貝葉斯方法;
   • 消極學習方法:KNN;區域性加權迴歸;基於案例的推理;

文獻資料

[1] Trevor Hastie & Rolbert Tibshirani. Discriminant Adaptive Nearest Neighbor Classification. IEEE TRANSACTIONS ON PAITERN ANALYSIS AND MACHINE INTELLIGENCE,1996.
[2] R. Short & K. Fukanaga. A New Nearest Neighbor Distance Measure,Pro. Fifth IEEE Int’l Conf.Pattern Recognition,pp.81-86,1980.
[3] T.M Cover. Nearest Neighbor Pattern Classification,Pro. IEEE Trans,Infomation Theory,1967.
[4] C.J.Stone. Consistent Nonparametric Regression ,Ann.Stat.,vol.3,No.4,pp.595-645,1977.
[5] W Cleveland. Robust Locally-Weighted Regression and Smoothing Scatterplots,J.Am.Statistical.,vol.74,pp.829-836,1979.
[6] T.A.Brown & J.Koplowitz. The Weighted Nearest Neighbor Rule for Class Dependent Sample Sizes,IEEE Tran. Inform.Theory,vol.IT-25,pp.617-619,Sept.1979.
[7] J.P.Myles & D.J.Hand. The Multi-Class Metric Problem in Nearest Neighbor Discrimination Rules,Pattern Recognition,1990.
[8] N.S.Altman. An Introduction to Kernel and Nearest Neighbor Nonparametric Regression,1992.
[9]Min-Ling Zhang & Zhi-Hua Zhou. M1-KNN:A Lazy Learning Approach to Multi-Label Learning,2007.
[10]Peter Hall,Byeong U.Park & Richard J. Samworth. Choice of Neighbor Order In Nearest Neighbor Classification,2008.
[11] Jia Pan & Dinesh Manocha. Bi-Level Locality Sensitive Hashing for K-Nearest Neighbor Computation,2012.