吳恩達卷積神經網路——卷積神經網路
計算機視覺
相關問題:
1)影象分類:

2)目標檢測:

3)影象風格遷移:

挑戰:資料輸入可能會非常大
輸入10001000的彩色影象,則需要輸入的資料量為100010003 =3M,這意味著特徵向量X的維度高達3M ,如果在第一隱藏層有1000個神經元,使用標準全連線,那麼權值矩陣中將會有10003M=3B的引數。引數量過於龐大,難以獲得足夠的資料用來防止過擬合,並且需要儲存3B資料的記憶體巨大,讓人無法接受。
卷積神經網可以處理大影象
邊緣檢測示例
卷積運算是卷積神經網路最基本的組成部分。
神經網路前幾層檢測邊緣,後面幾層檢測到物體的部分,更後面檢測到完整的物體。

計算機檢測目標時,最開始應是邊緣檢測,例如垂直邊緣或水平邊緣。
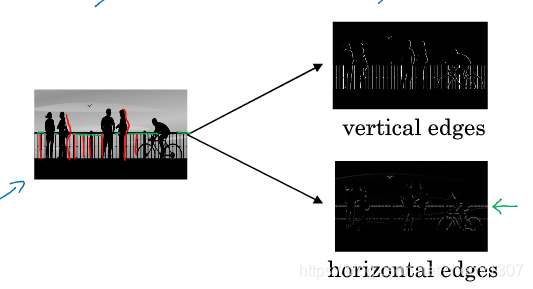
如何檢測邊緣?
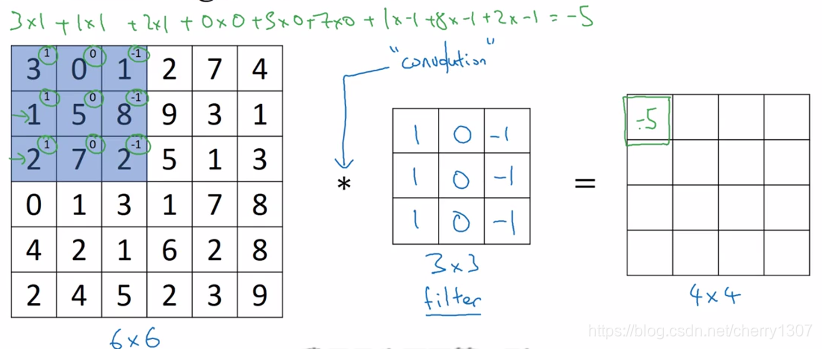
tensorflow
tf.nn.conv2d
邊緣檢測
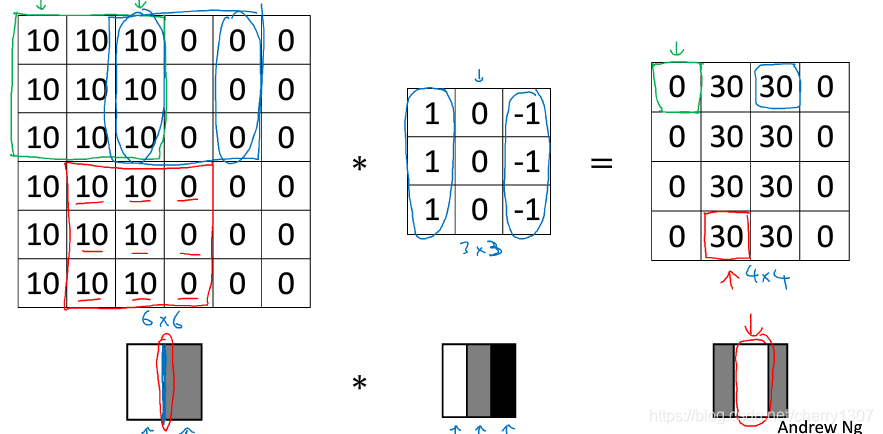
在輸出影象中間區域的亮出,表示在影象中間有一個特別明顯的垂直邊緣。
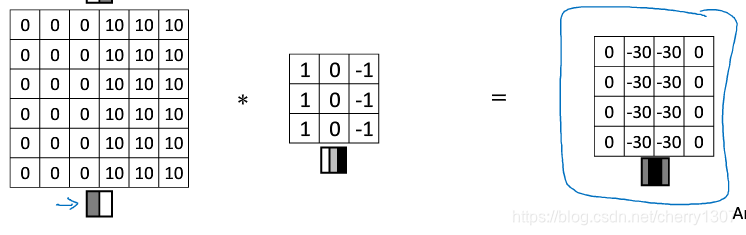
垂直邊緣檢測器:
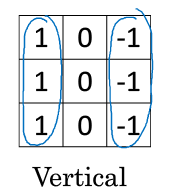
水平邊緣檢測器:
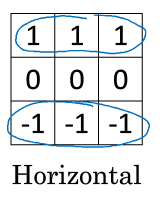
sobel:
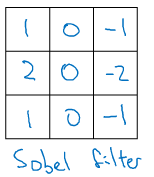
增加中間一行的權重使得結果的魯棒性更高
Padding
一個基本的卷積操作——padding
一個ff的卷積核取卷積一個66的影象。可能會得到一個(n-f+1)(n-f+1)的輸出。
缺點:
1.每次卷積操作,影象會縮小
2.角落的畫素點只被一個輸出所使用,丟失掉許多邊緣資訊。
為了解決這個問題,需要填充這幅影象(習慣上,用0填充)
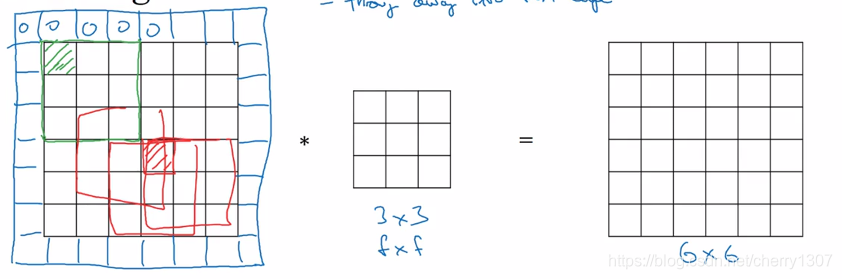
將66的影象填充為88輸出則為6
“Vaild” convolution:No padding:
nXn * fXf = n-f+1 X n-f+1
“Same” convolution:No padding:
nXn * fXf = n+2p-f+1 X n+2p-f+1
n+2p-f+1 =n
p = (f-1)/2(f一般為奇數)
卷積步長
卷積步長是卷積神經網路的基本操作
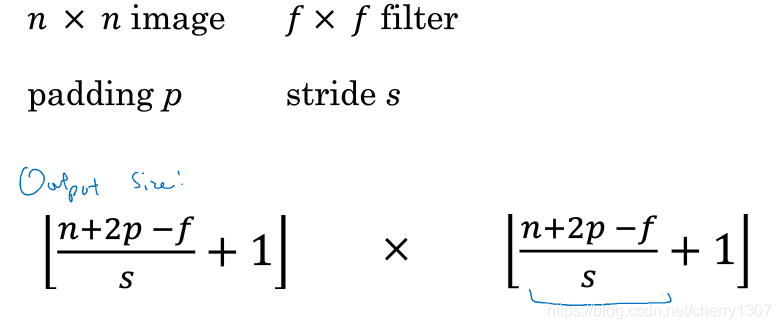
卷積為何有效
假設想檢測一個彩色影象的特徵,大小為66,三個通道,為了檢測影象的邊緣或一些其他特徵,不是把它和原來33的卷積核做卷積,而是和一個三維的卷積核做卷積。
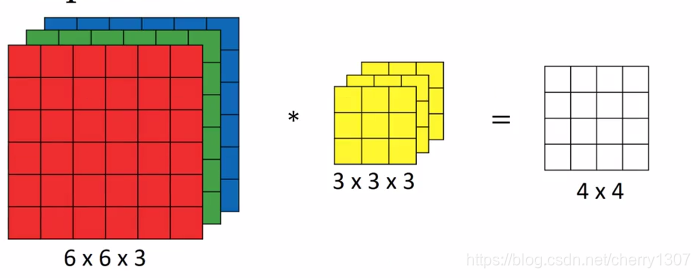
如果想檢測不同的特徵,用不同的卷積核:
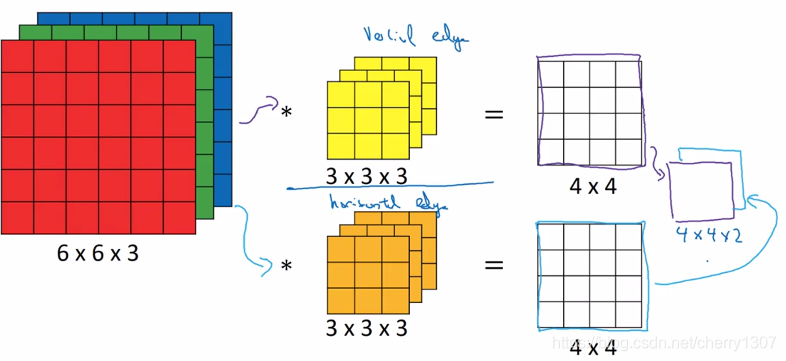
單層卷積網路
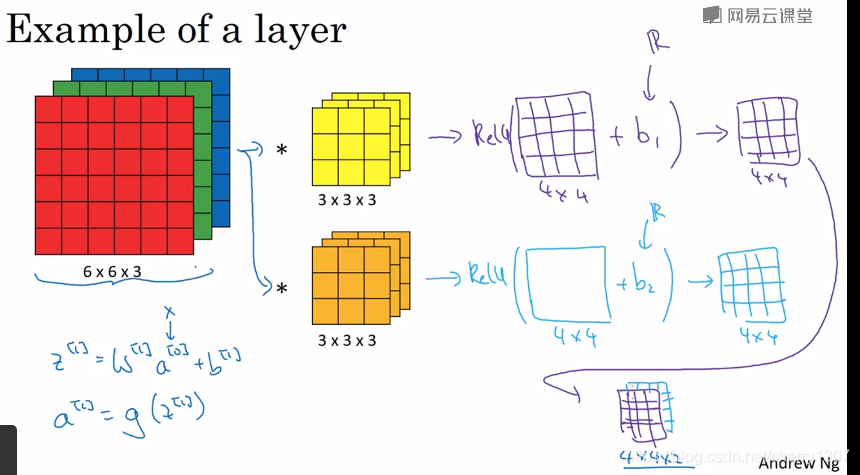
例如:10給我卷積核,大小為333,
引數=(333+1)*10=280
不論輸入影象有多大,引數只有280個,這就是卷積神經網路的一個特徵——“避免過擬合”
f^[l]:卷積核尺寸
p^[l]:padding
s^[l]:步長
nc^[l]:卷積核個數
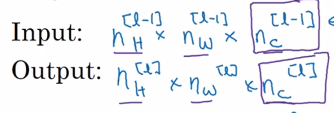
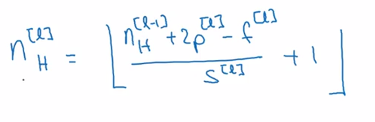
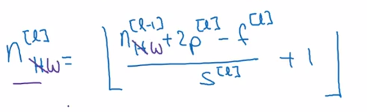
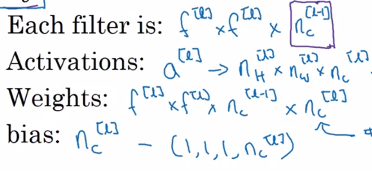
簡單卷積網路示例
要做影象分類或影象識別,輸入一張39393的影象,讓計算機識別影象中是否有貓

輸入39393
卷積核3310,stride=1 ,padding = 0
第一隱藏層:37373(39-3+1=37)
卷積核5520,stride=2 ,padding = 0
第二隱藏層:171720((37-5)/2+1=17)
卷積核5540,stride=2 ,padding = 0
第二隱藏層:7740((17-5)/2+1=7)
7740=1960
將全部1960個數字展開形成一個很長的向量,為了預測的結果將這個長向量填充到softmax迴歸函式中
隨著神經網路計算深度的不斷增加,影象不斷縮小,39->37->17->7,但通道數目不斷增加3->10->20->40
一個典型的CNN有:卷積層、池化層、全連線層
池化層
除了卷積層,CNN經常使用池化層縮減模型的大小,提高計算速度,同時提高所提取特徵的魯棒性。
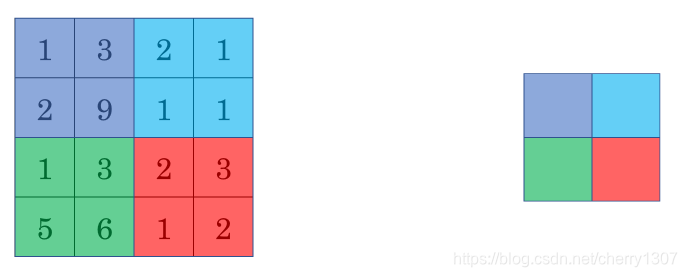
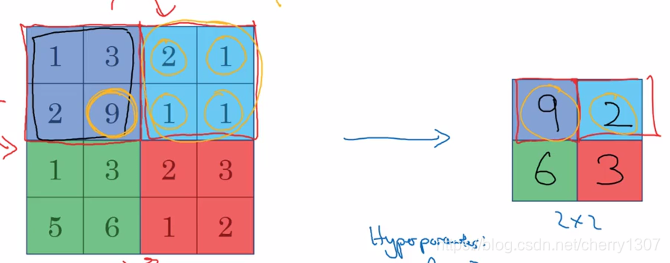
最大池化:
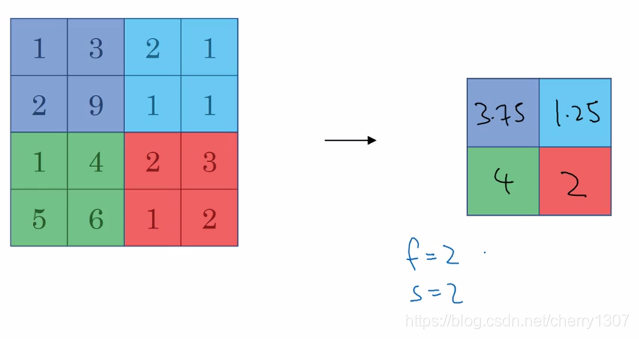
均值池化:
目前,用的最多的是最大池化
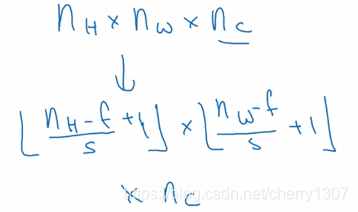
最大池化是計算神經網路某一層的靜態屬性
卷積神經網路示例(lenet-5)
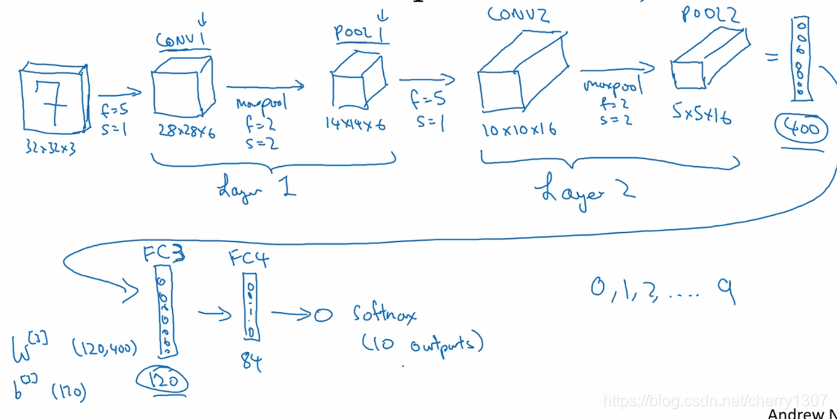
儘量不要自己設定超引數,檢視文獻中別人用了哪些超引數,選一個在別人任務中效果很好的架構,它有可能也適用於你自己的應用程式。
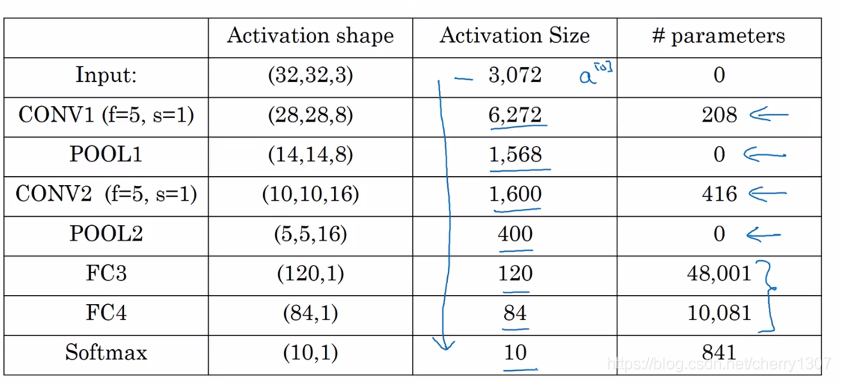
池化層沒有引數
卷積層引數少
隨著NN的加深,啟用值會減小,如果啟用值下降太快,也會影響網路效能
為什麼使用卷積?
引數少
原因:
1.引數共享
2.稀疏連線
