J. Straight Master

time limit per test

2.0 s

memory limit per test

256 MB

input

standard input

output

standard output

A straight is a poker hand containing five cards of sequential rank, not necessarily to be the same suit. For example, a hand containing 7 club, 6 spade, 5 spade, 4 heart and 3 diamond forms a straight. In this problem, we extend the definition of a straight to allow 3 to 5cards of sequential rank. Hence a hand containing K spade, Q club, and J heart is also a straight.

Mr. Panda is playing a poker game called Straight Master. The game uses a large deck of card that has N ranks from 1 to N. The rule of the game is simple: split the cards in Mr. Panda's hand into several straights of length from 3 to 5.

Now given a hand of cards, can you help Mr. Panda to determine if it is possible to split the cards into straights?

Input

The first line of the input gives the number of test cases, T. T test cases follow.

Each test case contains two lines. The first line contains an integer N, indicating the number of ranks in the deck. The next line contains N integers a1, a2, ..., aN indicating the number of cards for each rank in Mr. Panda's hand.

• 1 ≤ T ≤ 100.
• 1 ≤ N ≤ 2 × 105.
• 0 ≤ ai ≤ 109.
• .

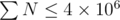Output

For each test case, output one line containing "Case #x: y", where x is the test case number (starting from 1) and y is Yes if Mr. Panda can split all his cards into straights of length from 3 to 5, or No otherwise.

Example

input

Copy

2
13
1 2 2 1 0 0 0 0 0 0 0 0 0
13
1 1 1 1 0 1 1 0 0 0 0 0 0

output

Copy

Case #1: Yes
Case #2: No

Note

In the first test case, Mr. Panda can split his cards into two straights: [1, 2, 3] and [2, 3, 4]. In the second test case, there is no way to form a straight for card 6 and 7.

3 4 5 的連續串能 -1  則大於3的連續串都能-1

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int mn = 2e5 + 10;
const ll mod = 1000000007;

ll a[mn], b[mn];
int main()
{
	int T;
	scanf("%d", &T);
	for (int cas = 1; cas <= T; cas++)
	{
		int n;
		scanf("%d", &n);
		for (int i = 1; i <= n; i++)
			scanf("%lld", &a[i]);
		
		a[n + 1] = 0;
		for (int i = 1; i <= n + 1; i++)
			b[i] = a[i] - a[i - 1];		/// 差分
		
		ll sum = 0;
		bool flag = 1;
		for (int i = 1; i <= n + 1; i++)
		{
			if (b[i] > 0)
				sum += b[i];
			if (i + 3 <= n + 1 && b[i + 3] < 0)
			{
				if ((sum + b[i + 3]) >= 0)
					sum += b[i + 3];
				else 
				{
					flag = 0;
					break;
				}
			}
		}
		if (sum)
			flag = 0;
		
		if (flag == 1)
			printf("Case #%d: Yes\n", cas);
		else 	
			printf("Case #%d: No\n", cas);
	}
	return 0;
}