【總結】插頭DP-bzoj1210/2310/2331/2595
首先感謝LadyLex的插頭DP:從零概念到入門,讓我對插頭DP的理解更進了一步。本文部分內容/圖片也轉錄於此。
概述
插頭DP主要用來處理一系列基於連通性 狀態壓縮 的動態規劃問題,處理的具體問題有很多種,並且一般資料規模較小。
插頭DP在棋盤模型上的應用最廣泛,非常考察思維的嚴謹性和全面性。
在基本的模板(雜湊/DP結構)的基礎上,插頭的變換和銜接成為了問題的關鍵。
基本方式
狀態確定
插頭
在插頭DP中,插頭表示一種聯通的狀態,以棋盤為例,一個格子有一個向某方向的插頭,就意味著這個格子在這個方向已經與外面相連(表示兩個相鄰格子之間已經格子聯通)。
前驅狀態對應的插頭必須接上,同時考慮接下來插頭的走向。
逐格遞推
對於第 行第 列的格子 :走向它的方案,可能由上一行的下插頭轉移而來,也可能是本行的右插頭轉移而來。
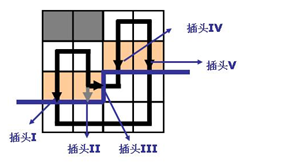
一如輪廓線DP,插頭 用狀態壓縮的方式記錄處理當前格時最近一排已決策格子的插頭情況。具體而言: ~ 列表示當前行已決策的下插頭,第 列表示 已決策的右插頭, 到最後一列分別表示上一行的下插頭。
如圖:紅色格子是最近一排已決策的格子,藍線是需要狀壓記錄的插頭狀態。
狀態轉移
行間轉移
設列數為 ,狀壓需要記錄的 個插頭下標分別為 。
一行處理完之後, 位分別代表每個下插頭,而轉移到下一行第一個格子時,應當由 位來表示,所以整體右移一位即可。
行內轉移
我們以最簡單的模型:用任意條簡單迴路遍歷整個棋盤的方案數。
注意到每個格子都處於迴路上,所以必然連線兩個的插頭。我們只需要維護狀態 ,分別表示有無插頭即可。
分類討論如下:
- 左上均無插頭,則右下均設立插頭
- 只有左或上有插頭,則將插頭拐彎或直走,分別判斷會不會走到邊界情況後轉移。
- 左上均有插頭,合併兩個插頭,不再向右下設立插頭。
在處理完所有格子後,所以狀態為0的即可計入答案。
程式碼實現
往往因為某些題目的特殊要求,我們需要設定大於2種的插頭,而種數有時並不是2的整次冪,種數進位制下狀態壓縮中轉碼和壓縮的效率很低,所以依舊以不小於種數的最小2的整次冪作為進位制處理。
而在轉移中,存在大量無用的不合法狀態,這時就需要雜湊表來儲存所有合法狀態。
struct Hs{
int val[mod],key[mod],hs[mod],sz;
inline void itia(){
memset(val,0,sizeof(val));//根據題目要求初始化
memset(key,0xff,sizeof(key));
memset(hs,0,sizeof(hs));sz=0;
}
inline void nh(int u,int v){key[++sz]=v;hs[u]=sz;}
int &operator [](const int S){
for(int i=S%mod;;i=(i+1==mod)?0:(i+1)){
if(!hs[i]) nh(i,S);
if(key[hs[i]]==S) return val[hs[i]];
}
}
}f[2];
而轉碼通常以函式形式寫出(設進製為4):
inline int gt(int S,int pos){return ((S>>((pos-1)<<1))&3);}
inline void sett(int &S,int pos,int v)
{pos=(pos-1)<<1;S|=(3<<pos);S^=(3<<pos);S|=(v<<pos);}
常見模型
常見的幾種插頭設定方式:
- 括號匹配
- 獨立插頭
- 最小表示法
1.bzoj1210: [HNOI2004]郵遞員
求一遍遍歷整個棋盤的簡單迴路的方案數。
相比用任意條簡單迴路遍歷整個棋盤,這道題對於左上都有插頭的情況多了一個限制:除非是右下角,否則兩插頭不能處於同一聯通塊。
於是我們可以用最小表示法來進行轉移:用不同標號表示不同的聯通既可。
但觀察下面的圖:
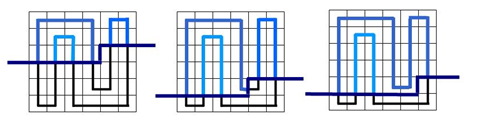
可以發現,輪廓線上方的路徑是由若干條互不相交的路徑構成了。而且每條路徑在輪廓線上存在對應的兩個插頭。
於是可以用括號匹配表示插頭。1,2分別表示左右插頭。它們最近的相異插頭就是對應的相同聯通塊的另一個插頭。
#include<bits/stdc++.h>
using namespace std;
const int N=(1<<20)+10,bs=1e9;
const int mod=2601;
int n,m,pr,pt=1;
struct bint{
int bit[7];
inline void clr(){memset(bit,0,sizeof(bit));}
bint(){clr();}
inline void sett(int x){for(clr();x;x/=bs)bit[++bit[0]]=x%bs;}
void operator =(int x){sett(x);}
int &operator [](int x){return bit[x];}
bint operator +(bint ky){
bint re;re.clr();int i,j;
j=re[0]=max(bit[0],ky[0])+1;
for(i=1;i<=j;++i){
re[i]+=bit[i]+ky[i];
re[i+1]+=re[i]/bs;re[i]%=bs;
}
for(;re[0]>0 && (!re[re[0]]);--re[0]);
return re;
}
void operator +=(bint ky){*this=*this+ky;}
inline void prit(){
printf("%d",bit[bit[0]]);
for(int i=bit[0]-1;i>0;--i) printf("%09d",bit[i]);
}
}ans;
struct Hs{
bint val[mod];int key[mod],hs[N],sz;
inline void itia(){
memset(val,0,sizeof(val));memset(key,0xff,sizeof(key));
memset(hs,0,sizeof(hs));sz=0;
}
inline void nh(int u,int v){key[++sz]=v;hs[u]=sz;}
bint &operator [](const int sta){
for(int i=sta%mod;;i=(i+1==mod)?0:(i+1)){
if(!hs[i]) nh(i,sta);
if(key[hs[i]]==sta) return val[hs[i]];
}
}
}f[2];
inline int gt(int S,int pos){return ((S>>((pos-1)<<1))&3);}
inline void sett(int &S,int pos,int vl)
{pos=(pos-1)<<1;S|=(3<<pos);S^=(3<<pos);S|=(vl<<pos);}
inline int fd(int S,int pos)
{
int i,j,cot=0,delta=(gt(S,pos)==1)?1:(-1);
for(i=pos;i&&(i<=m+1);i+=delta){
j=gt(S,i);
if(j==1) cot--;else if(j==2) cot++;
if(!cot) return i;
}
return -1;
}
inline void cal(int x,int y)
{
pr^=1;pt^=1;f[pr].itia();
int k,S,a,b;bint vl;
for(k=f[pt].sz;k;--k){
S=f[pt].key[k];vl=f[pt].val[k];
if(fd(S,y)==-1 || fd(S,y+1)==-1) continue;
a=gt(S,y);b=gt(S,y+1);
if((!a)&&(!b)){if(x<n && y<m) sett(S,y,1),sett(S,y+1,2),f[pr][S]+=vl;}
else if((!a)&&b){
if(y<m) f[pr][S]+=vl;//turn right
if(x<n){sett(S,y,b);sett(S,y+1,0);f[pr][S]+=vl;}//turn down
}else if(a&&(!b)){
if(x<n) f[pr][S]+=vl;//turn down
if(y<m){sett(S,y,0);sett(S,y+1,a);f[pr][S]+=vl;}//turn right
}else if((a==1)&&(b==1)){
sett(S,fd(S,y+1),1);sett(S,y,0);sett(S,y+1,0);f[pr][S]+=vl;
}else if((a==1)&&(b==2)){if((x==n)&&(y==m)) ans+=vl;}
else if((a==2)&&(b==1)){
sett(S,y,0);sett(S,y+1,0);f[pr][S]+=vl;
}else if((a==2)&&(b==2)){
sett(S,fd(S,y),2);sett(S,y,0);sett(S,y+1,0);f[pr][S]+=vl;
}
}
}
int main(){
int i,j;
scanf("%d%d",&n,&m);
if(m>n) swap(n,m);
if(m==1) {putchar('1');return 0;}
f[0].itia();f[0][0]=1;
for(i=1;i<=n;++i){
for(j=1;j<=m;++j) cal(i,j);
if(i==n) break;
for(j=f[pr].sz;j;--j) f[pr].key[j]<<=2;
}
ans=ans+ans;ans.prit();
return 0;
}
2.bzoj2310: ParkII
求一條簡單路徑,使得經過的點權值之和最大。
建2個獨立插頭(也就是沒有對應左右插頭),延伸即可。
#include<bits/stdc++.h>
using namespace std;
const int mod=22787;
int g[102][10],n,m;
int ans,pr,pt=1;
struct Hs{
int key[mod],sz,val[mod],hs[mod];
inline void itia(){
memset(key,0xff,sizeof(key));memset(val,0x8f,sizeof(val));
sz=0;memset(hs,0,sizeof(hs));
}
inline int nh(int u,int v){key[++sz]=v;hs[u]=sz;}
inline int &operator [](const int S){
for(int i=S%mod;;i=(i+1==mod)?0:(i+1)){
if(!hs[i]) nh(i,S);
if(key[hs[i]]==S) return val[hs[i]];
}
}
}f[2];
inline int gt(int S,int pos){return ((S>>((pos-1)<<1))&3);}
inline void sett(int &S,int pos,int vl)
{pos=(pos-1)<<1;S|=(3<<pos);S^=(3<<pos);S|=(vl<<pos);}
inline int fd(int S,int pos)
{
int i,j,cot=0,delta=(gt(S,pos)==1)?1:(-1);
for(i=pos;i&&(i<=m+1);i+=delta){
j=gt(S,i);
if(j==1) cot--;else if(j==2) cot++;
if(!cot) return i;
}
return -1;
}
inline bool ck(int S)
{
int i,j,cot=0,cnt=0;
for(i=0;i<=m;++i,S>>=2){
j=S&3;
if(j==3) cnt++;
else if(j==1) cot--;
else if(j==2) cot++;
}
return ((cnt>2)||(cot!=0));
}
inline void upp(int &x,int y){x=(y>x)?y:x;}
inline void cal(int x,int y)
{
pr^=1;pt^=1;f[pr].itia();
int i,j,k,t,S,res,vl,a,b;
for(i=f[pt].sz;i;--i){
S=f[pt].key[i];vl=f[pt].val[i];
a=gt(S,y);b=gt(S,y+1);
if(ck(S)||(S>=(1<<((m+1)<<1)))) continue;
vl+=g[x][y];
if((!a)&&(!b)){
upp(f[pr][S],vl-g[x][y]);
if((x<n)&&(y<m)){res=S;sett(res,y,1);sett(res,y+1,2);upp(f[pr][res],vl);}
if(x<n){res=S;sett(res,y,3);upp(f[pr][res],vl);
if(y<m){sett(S,y+1,3);upp(f[pr][S],vl);}
}else if((!a)&&b){
if(y<m) upp(f[pr][S],vl);
if(x<n){res=S;sett(res,y,b);sett(res,y+1,0);upp(f[pr][res],vl);}
if(b==3){if(S==(b<<(y<<1))) upp(ans,vl);}
else{sett(S,fd(S,y+1),3);sett(S,y+1,0);upp(f[pr][S],vl);}
}else if(a&&(!b)){
if(x<n) upp(f[pr][S],vl);
if(y<m){res=S;sett(res,y,0);sett(res,y+1,a);upp(f[pr][res],vl);}
if(a==3){if(S==(a<<((y-1)<<1))) upp(ans,vl);}
else{sett(S,fd(S,y),3);sett(S,y,0);upp(f[pr][S],vl);}
}
else if((a==1)&&(b==1)){sett(S,fd(S,y+1),1);sett(S,y,0);sett(S,y+1,0);upp(f[pr][S],vl);}
else if((a==2)&&(b==1)){sett(S,y,0);sett(S,y+1,0);upp(f[pr][S],vl);}
else if((a==2)&&(b==2)){sett(S,fd(S,y),2);sett(S,y,0);sett(S,y+1,0);upp(f[pr][S],vl);}
else if((a==3)&&(b==3)){sett(S,y,0);sett(S,y+1,0);if(!S) upp(ans,vl);}
else if(a==3){sett(S,fd(S,y+1),3);sett(S,y,0);sett(S,y+1,0);upp(f[pr][S],vl);}
else if(b==3){sett(S,fd(S,y),3);sett(S,y,0);sett(S,y+1,0);upp(f[pr][S],vl);}
}
}
int main(){
int i,j;
scanf("%d%d",&n,&m);
for(i=1;i<=n;++i)
for(j=1;j<=m;++j)
scanf("%d",&g[i][j]),ans=max(ans,g[i][j]);
f[0].itia();f[0][0]=0;
for(i=1;i<=n;++i){
for(j=1;j<=m;++j) cal(i,j);
if(i==n) break;
for(j=f[pr].sz;j;--j) f[pr].key[j]<<=2;
}
printf("%d\n",ans);
return 0;
}
3.bzoj2331: [SCOI2011]地板
求用L型的地板鋪滿整個客廳的方案數。
設 分別表示沒有插頭,沒有拐過彎的插頭,拐過彎的插頭即可。
#include<bits/stdc++.h>
using namespace std;
const int mod=20110520,bs=200097;
int n,m,pr,pt=1,ans,lsx,lsy;
char bn[105][105],rq[105];
inline void ad(int &x,int y){x+=y;if(x>=mod) x-=mod;}
struct Hs{
int val[bs],sz,key[bs],hs[bs];
inline void itia(){
memset(val,0,sizeof(val));memset(key,0xff,sizeof(key));
memset(hs,0,sizeof(hs));sz=0;
}
inline void nh(int u,int v){key[++sz]=v;hs[u]=sz;}
int &operator [](const int S){
for(int i=S%bs;;i=(i+1==bs)?0:(i+1)){
if(!hs[i]) nh(i,S);
if(key[hs[i]]==S) return val[hs[i]];
}
}
}f[2];
inline void init()
{
int i,j;
scanf("%d%d",&n,&m);
if(m>n){
for(i=1;i<=n;++i){
scanf("%s",rq+1);
for(j=1;j<=m;++j)
bn[j][n+1-i]=rq[j];
}
swap(n,m);
}else for(i=1;i<=n;++i) scanf("%s",bn[i]+1);
for(i=1;i<=n;++i)
for(j=1;j<=m;++j){
bn[i][j]=(bn[i][j]!='*');
if(bn[i][j]) lsx=i,lsy=j;
}
}
inline int gt(int S,int pos){return ((S>>((pos-1)<<1))&3);}
inline void sett(int &S,int pos,int v)
{pos=(pos-1)<<1;S|=(3<<pos);S^=(3<<pos);S|=(v<<pos);}
inline void cal(int x,int y)
{
pr^=1;pt^=1;f[pr].itia();
int i,j,k,S,res,vl;
for(k=f[pt].sz;k;--k){
S=f[pt].key[k];vl=f[pt].val[k];
i=gt(S,y);j=gt(S,y+1);
if(bn[x][y]){
if((!i)&&(!j)){
if(bn[x+1][y]){res=S;sett(res,y,1);ad(f[pr][res],vl);}
if(bn[x][y+1]){res=S;sett(res,y+1,1);ad(f[pr][res],vl);}
if(bn[x+1][y]&&bn[x][y+1]){sett(S,y,2);sett(S,y+1,2);ad(f[pr][S],vl);}
}else if(i&&(!j)){
if(bn[x][y+1]){res=S;sett(res,y,0);sett(res,y+1,i);ad(f[pr][res],vl);}
if(i==1 && bn[x+1][y]){sett(S,y,2);ad(f[pr][S],vl);}
else if(i==2){
sett(S,y,0);ad(f[pr][S],vl);
if((x==lsx)&&(y==lsy)&&(!S)) ad(ans,vl);
}
}else if((!i)&&j){
if(bn[x+1][y]){res=S;sett(res,y+1,0);sett(res,y,j);ad(f[pr][res],vl);}
if(j==1 && bn[x][y+1]){sett(S,y+1,2);ad(f[pr][S],vl);}
else if(j==2){
sett(S,y+1,0);ad(f[pr][S],vl);
if((x==lsx)&&(y==lsy)&&(!S)) ad(ans,vl);
}
}else if((i==1)&&(j==1)){
sett(S,y,0);sett(S,y+1,0);ad(f[pr][S],vl);
if((x==lsx)&&(y==lsy)&&(!S)) ad(ans,vl);
}
}else if((!i)&&(!j)) ad(f[pr][S],vl);
}
}
int main(){
int i,j;init();
f[0].itia();f[0][0]=1;
for(i=1;i<=n;++i){
for(j=1;j<=m;++j) cal(i,j);
if(i==n) break;
for(j=f[pr].sz;j;--j) f[pr].key[j]<<=2;
}
printf("%d",ans);
return 0;
}
4.bzoj2595: [Wc2008]遊覽計劃
最小表示法維護聯通塊即可。
題解
