深度學習: Dropout
Dropout: A simple Way to Prevent Neural Networks from Overfitting
摘要
過擬合是機器學習領域較為突出的問題之一,很多方法已提出用於緩解過擬合。該文提出的方法是Dropout(剔除、刪除等翻譯即可)。只需記住一句話即可: 在神經網路訓練過程中隨機刪除一些啟用單元以及與這些啟用單元相連的邊,這避免了啟用單元之間過多的協同適應(生物學解釋: In biology, co-adaptation is the process by which two or more species, genes or
引言
這部分提出通過窮舉所有可能的神經網路模型引數設定,對每種引數設定進行加權,再平均化。或者,通過整合學習的方式提高模型泛化能力。但是這兩種方法,一個是天方夜譚(想想神經網路的規模吧),一個是計算量太大,均不可取。但是該文引入的Dropout卻同時具有計算量小且有近似整合學習的功效(後面介紹原因)。
首先來看一下應用Dropout前後的神經網路,如下:
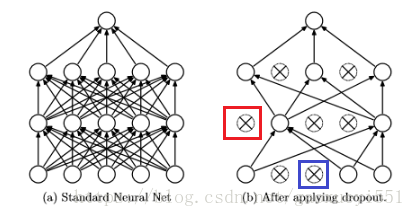 圖 1
Dropout前後對比
圖 1
Dropout前後對比
以上圖為例,可以看到這是一個由輸入層,兩個隱層和輸出層組成的神經網路。部分啟用單元連同輸入和輸出一併被刪除。那麼Dropout的機制是怎樣的那?
首先, 為每一層(輸出層除外)單獨設定一個概率值 (
表示層索引 ) 作為該層的啟用單元保留下來的概率,隱層(紅色標註處)的概率一般設定為0.5,輸入層(藍色標註處)一般設定為較接近1的值(這可能是為了儘可能多的捕獲輸入特徵)。每層設定完之後,可能是:(0.8, 0.5, 0.5)
下面簡單解釋Dropout具有整合學習效應的原因。應用Dropout到神經網路可以看做從原始神經網路中抽取一個更為“稀疏”的神經網路,一個具有 個啟用單元的神經網路最多大約可以抽出
個“稀疏”的神經網路,將訓練過程中產生的所有“稀疏”神經網路的引數按照一定策略進行加權,產生最終的模型,這正是整合學習的要義所在!
使用Dropout訓練神經網路
神經網路一般通過Mini-Batch和梯度下降進行訓練,加入Dropout後依然如此。不同之處在於在每次Mini-Batch訓練之前,從當前的神經網路中抽出一個“稀疏”的神經網路進行前向和反向傳播,若經過 次Mini-Batch過後模型引數收斂到一定誤差之內,則此時產生了
個不同的“稀疏”神經網路,每個“稀疏”的神經網路的結構可能不同,如下圖所示:
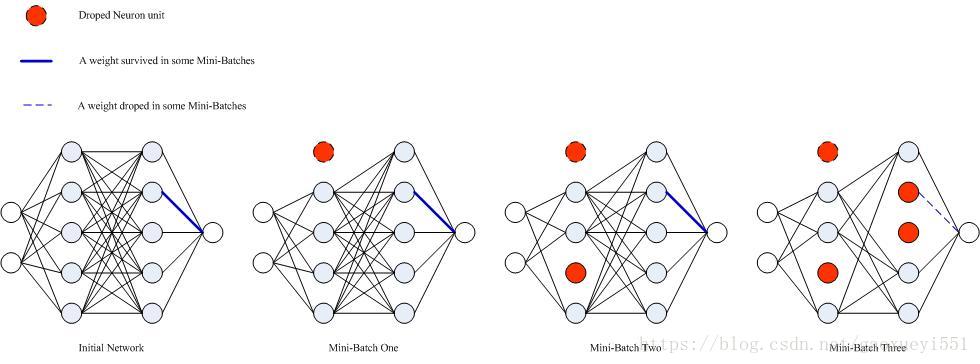 圖 2 Dropout神經網路訓練過程中產生的“稀疏”神經網路
圖 2 Dropout神經網路訓練過程中產生的“稀疏”神經網路
引數的更新規則是將所有“稀疏”神經網路中對應位置的引數的梯度值進行平均,作為最終模型該引數的最終梯度值。其中,若某一引數未出現在某一“稀疏”神經網路中,則該“稀疏”神經網路對應的引數梯度值為0。如圖,設 初始值為 0.8,Mini-Batch One對應該引數的梯度值為 0.9,Mini-Batch Two對應該引數的梯度值為 0.7,Mini-Batch Three中對應該引數的梯度值為 0,若此時模型已收斂到誤差範圍之內(實際訓練過程中還會經歷多次epoch,這裡僅用一次epoch進行簡化說明),則該引數對應的梯度值為
。結合上圖以及引數的更新規則可以直觀感受到Dropout具有的整合學習效應。
Dropout神經網路的前向傳播過程
這裡重點介紹一下Dropout神經網路的前向傳播過程,其反向傳播過程與沒有使用Dropout的神經網路訓練過程相同。其前向傳播公式如下:
為層索引,
,
為某一層中的啟用單元索引,
為第
層中的第
個啟用單元設定的隨機保留(
等於1)概率,與未使用Dropout的神經網路前向傳播差別在於公式(1)和(2)。
訓練Dropout神經網路的一些建議
- Dropout rate(刪除比率): 試資料集規模而定。
- Dropout神經網路由於在前後傳播中引入較多的噪音,啟用單元之間的梯度值會發生相互抵消的 現象,為此,Dropout神經網路的學習率應該是非Dropout神經網路學習率的10-100倍,或者使用0.95-0.99之間的一個動量值。
- Dropout + Max-norm Regularization: 加上Max-norm Regularization,是為了保持建議2的優勢之外,權重不會因為學習率過大而出現爆炸。半徑值一般設未3-4之間。
