複習筆記-排序演算法
阿新 • • 發佈:2018-11-27
目錄
1. \(O\left ( N^2 \right )\)
- 選擇排序
- 氣泡排序
2. \(O\left (N \log N \right )\)(重點)
- 歸併排序
- 快速排序
- 堆排序
3.\(O \left ( N \right )\)(重點)
- 桶排
一、 \(O\left ( N^2 \right )\)
\(\left ( 1\right )\)選擇排序(不穩定)
1.原理:判斷這個數以後的所有數,將小的放在前面,如果沒有,就swap(挖坑)
2.考點:複賽基本不用,初賽要考
3.關鍵程式碼:
for(int i=1;i<=N;i++) { for(int j=i+1;j<=N;j++) { if(a[i]>a[j]) { swap(a[i],a[j]); } } }
4.時間複雜度:
最好情況: \(O\left ( N \right )\)
最壞情況: \(O\left ( N^2 \right )\)
平均情況: \(O\left ( N^2 \right )\)

***
\(\left ( 2\right )\) 氣泡排序(不穩定)
1.原理:比較相鄰的元素,將小的放在前面
2.考點:初賽重點
3.關鍵程式碼:(初始程式碼)
for(int i=1;i<=N;i++) { for(int j=1;j<=N-i;j++) { if(a[j]>a[j+1]) { swap(a[j],a[j+1]); } } }
還可以優化一下,當發現沒有交換,就跳出迴圈
bool flag = true;
int k = n;
while(flag)
{
flag = false;
for(int i=1;i<=k;i++)
{
if(a[i]>a[i+1])
{
swap(a[i],a[i+1]);
flag = true;
}
}
k--;
}4.時間複雜度
最好情況: \(O\left ( N \right )\)
最壞情況: \(O\left ( N^2 \right )\)
平均情況: \(O\left ( N^2 \right )\)

二、 \(O\left ( N\log N \right )\)
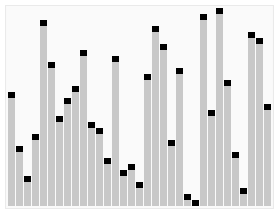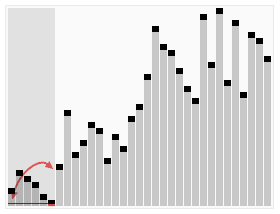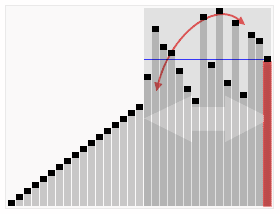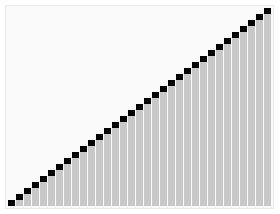
\(\left ( 1\right )\)快速排序(不穩定)
1.原理:氣泡排序的改進,用二分的思想進行優化
2.考點:幾乎所有時候,快排都能過(除了卡快排的題 如P1309 瑞士輪||資料太大的題)
3.優化:三平均分割槽法
(以下摘自百度)
關於這一改進的最簡單的描述大概是這樣的:與一般的快速排序方法不同,它並不是選擇待排陣列的第一個數作為中軸,而是選用待排陣列最左邊、最右邊和最中間的三個元素的中間值作為中軸。這一改進對於原來的快速排序演算法來說,主要有兩點優勢:
①首先,它使得最壞情況發生的機率減小了。
②其次,未改進的快速排序演算法為了防止比較時陣列越界,在最後要設定一個哨點。
4.關鍵程式碼:
①STL自帶函式
sort(a+1,a+n+1); //a為陣列名(預設從小到大)可以配合cmp函式使用
bool cmp(int x,int y){return x>y;}//(從大到小cmp)結構體排序可以使用cmp函式,也可使用過載運算子
cmp
struct node
{
int id,v;
};
bool cmp(node x,node y)
{
if(x.v>y.v) return 1;
else if(x.id<y.id) return 1;
return 0;
}過載運算子
struct node
{
int id,v;
bool operator <(const node &n)const
{
if(v>n.v) return 1;
else if(id<n.id) return 1;
return 0;
}
};②自己寫二分(不推薦,既然有了STL,還要什麼二分)
(以下摘自Hardict大佬)
void swap(int arr[], int i, int j)
{
int temp;
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
void QuickSort(int arr[], int left, int right)
{
int i, pivot;
if (left >= right)
return;
pivot = left;
swap(arr, left, (left + right) / 2);
for (i = left + 1; i <= right; i++) //單邊搜尋,可以該為雙向搜尋(據說快點( ° ▽、° ))
if (arr[i] < arr[left])
swap(arr, i, ++pivot);
swap(arr, left, pivot);
QuickSort(arr, left, pivot - 1);
QuickSort(arr, pivot + 1, right);
}5.時間複雜度:
最壞情況: \(O\left ( N^2 \right )\)
最好情況: \(O\left ( N\log N \right )\)
平均情況: \(O\left ( N\log N \right )\)
***
\(\left ( 2\right )\)歸併排序(穩定)
1.原理:運用分治法,將兩個數列合併,再將這兩個數列分開
(以下轉自MoreWindows大佬)
首先考慮下如何將將二個有序數列合併。這個非常簡單,只要從比較二個數列的第一個數,誰小就先取誰,取了後就在對應數列中刪除這個數。然後再進行比較,如果有數列為空,那直接將另一個數列的資料依次取出即可。
解決了上面的合併有序數列問題,再來看歸併排序,其的基本思路就是將陣列分成二組A,B,如果這二組組內的資料都是有序的,那麼就可以很方便的將這二組資料進行排序。如何讓這二組組內資料有序了?
可以將A,B組各自再分成二組。依次類推,當分出來的小組只有一個數據時,可以認為這個小組組內已經達到了有序,然後再合併相鄰的二個小組就可以了。這樣通過先遞迴的分解數列,再合併數列就完成了歸併排序。
2.考點:在快排不能用時,就用它(如 P1309 瑞士輪)
3.關鍵程式碼
①STL實現
將兩個數組合並放到第三個陣列(其實是歸併排序的一部分:並)
merge(w+1,w+1+wn,l+1,l+1+ln,p+1,cmp);//w為第一個陣列,l為第二個陣列,p為合併後放入的陣列,wn,ln分別為w[],l[]的長度一個數組歸併排序
int a[100000];
int mergesort(int l,int r)
{
if(l>=r) return 0;
int mid(l+r)/2;
mergesort(l,mid);
mergesort(mid+1,r);
inplace_merge(a+l,a+mid+1,a+r+1);//STL庫自帶函式
}
mergesort(a+1,a+n+1);//排序②手寫歸併排序(兩個陣列歸併排序)
(以下同樣摘自MoreWindows大佬)
//將有二個有序數列a[first...mid]和a[mid...last]合併。
void mergearray(int a[], int first, int mid, int last, int temp[])
{
int i = first, j = mid + 1;
int m = mid, n = last;
int k = 0;
while (i <= m && j <= n)
{
if (a[i] <= a[j])
temp[k++] = a[i++];
else
temp[k++] = a[j++];
}
while (i <= m)
temp[k++] = a[i++];
while (j <= n)
temp[k++] = a[j++];
for (i = 0; i < k; i++)
a[first + i] = temp[i];
}
void mergesort(int a[], int first, int last, int temp[])
{
if (first < last)
{
int mid = (first + last) / 2;
mergesort(a, first, mid, temp); //左邊有序
mergesort(a, mid + 1, last, temp); //右邊有序
mergearray(a, first, mid, last, temp); //再將二個有序數列合併
}
}
bool MergeSort(int a[], int n)
{
int *p = new int[n];
if (p == NULL)
return false;
mergesort(a, 0, n - 1, p);
delete[] p;
return true;
}4.時間複雜度
歸併的歸:\(O\left ( \log N \right )\)
歸併的並:\(O\left ( N \right )\)
總時間複雜度:\(O\left ( N\log N \right )\)(基本穩定)

***
\(\left ( 3\right )\)堆排序(不穩定)
1.原理:利用了大根堆(或小根堆)的堆頂記錄關鍵字最大(或最小)的特性,專門設計的一種排序,屬於選排的一種(堆是一種完全二叉樹)
(以下摘自百度)
用大根堆排序的基本思想
① 先將初始檔案R[1..n]建成一個大根堆,此堆為初始的無序區
② 再將關鍵字最大的記錄R[1](即堆頂)和無序區的最後一個記錄R[n]交換,由此得到新的無序區R[1..n-1]和有序區R[n],且滿足R[1..n-1].keys≤R[n].key
③由於交換後新的根R[1]可能違反堆性質,故應將當前無序區R[1..n-1]調整為堆。然後再次將R[1..n-1]中關鍵字最大的記錄R[1]和該區間的最後一個記錄R[n-1]交換,由此得到新的無序區R[1..n-2]和有序區R[n-1..n],且仍滿足關係R[1..n-2].keys≤R[n-1..n].keys,同樣要將R[1..n-2]調整為堆。
……
直到無序區只有一個元素為止。
2.考點:用於常數大的時候(Dijkstra,Prim時要用)如: P1843 奶牛晒衣服
3.關鍵程式碼:
①STL實現
優先佇列(預設從大到小,如果需從小到大,需用結構體+過載運算子)
priority_queue<int>qu;
for(int i=1;i<=N;i++)
{
qu.push(a[i]);
}
for(int i=1;i<=N;i++)
{
a[i]=qu.front();
}小根堆實現(預設從大到小,如果需從小到大,需用結構體+過載運算子)//比優先佇列快
struct node
{
int x;
bool operator <(const node &n)const
{
return x<n.x;
}
};
node heap[N];
int heaplen=0;
int pushHeap(int x)
{
heap[heaplen].x=x;
heaplen++;
push_heap(heap,heap+heaplen);
}
int popHeap()
{
pop_heap(heap,heap+heaplen);
heaplen--;
return heap[heaplen].x;
}
for(int i=1;i<=N;i++)
{
pushHeap(a[i]);
}
for(int i=1;i<=N;i++)
{
a[i]=popHeap();
}②自建堆(小根堆)
(以下摘自MoreWindows大佬)
堆的插入:
// 新加入i結點 其父結點為(i - 1) / 2
void MinHeapFixup(int a[], int i)
{
int j, temp;
temp = a[i];
j = (i - 1) / 2; //父結點
while (j >= 0 && i != 0)
{
if (a[j] <= temp)
break;
a[i] = a[j]; //把較大的子結點往下移動,替換它的子結點
i = j;
j = (i - 1) / 2;
}
a[i] = temp;
}
//在最小堆中加入新的資料nNum
void MinHeapAddNumber(int a[], int n, int nNum)
{
a[n] = nNum;
MinHeapFixup(a, n);
} 堆的刪除:
// 從i節點開始調整,n為節點總數 從0開始計算 i節點的子節點為 2*i+1, 2*i+2
void MinHeapFixdown(int a[], int i, int n)
{
int j, temp;
temp = a[i];
j = 2 * i + 1;
while (j < n)
{
if (j + 1 < n && a[j + 1] < a[j]) //在左右孩子中找最小的
j++;
if (a[j] >= temp)
break;
a[i] = a[j]; //把較小的子結點往上移動,替換它的父結點
i = j;
j = 2 * i + 1;
}
a[i] = temp;
}
//在最小堆中刪除數
void MinHeapDeleteNumber(int a[], int n)
{
Swap(a[0], a[n - 1]);
MinHeapFixdown(a, 0, n - 1);
}堆的建立、插入與刪除圖解
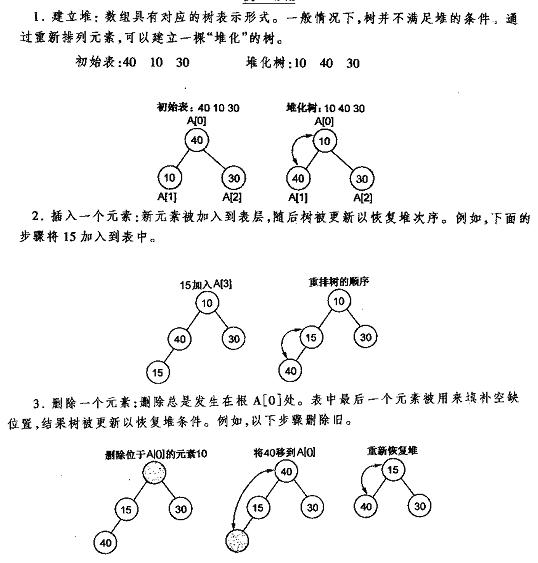
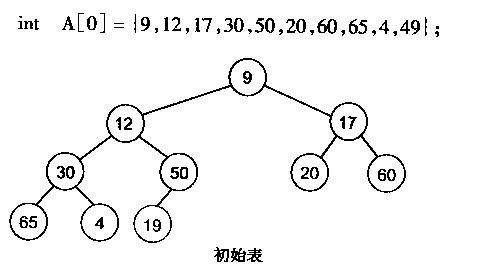
堆化陣列程式碼及圖解:
//建立最小堆
void MakeMinHeap(int a[], int n)
{
for (int i = n / 2 - 1; i >= 0; i--)
MinHeapFixdown(a, i, n);
}
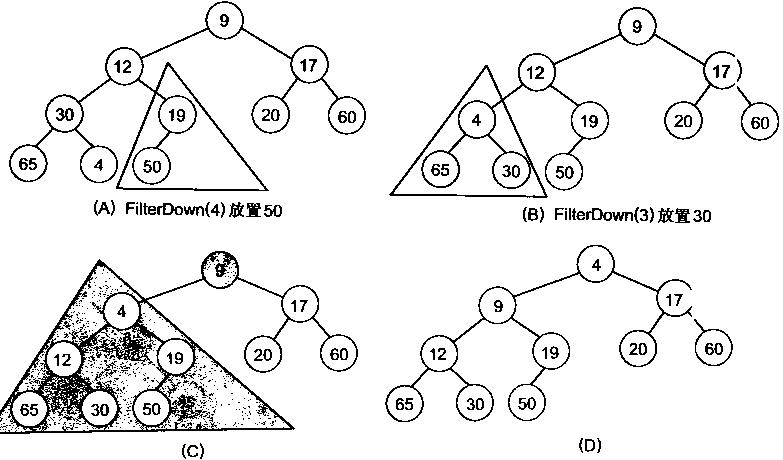
堆排序:
// 新加入i結點 其父結點為(i - 1) / 2
void MinHeapFixup(int a[], int i)
{
int j, temp;
temp = a[i];
j = (i - 1) / 2; //父結點
while (j >= 0 && i != 0)
{
if (a[j] <= temp)
break;
a[i] = a[j]; //把較大的子結點往下移動,替換它的子結點
i = j;
j = (i - 1) / 2;
}
a[i] = temp;
}
//在最小堆中加入新的資料nNum
void MinHeapAddNumber(int a[], int n, int nNum)
{
a[n] = nNum;
MinHeapFixup(a, n);
}
// 從i節點開始調整,n為節點總數 從0開始計算 i節點的子節點為 2*i+1, 2*i+2
void MinHeapFixdown(int a[], int i, int n)
{
int j, temp;
temp = a[i];
j = 2 * i + 1;
while (j < n)
{
if (j + 1 < n && a[j + 1] < a[j]) //在左右孩子中找最小的
j++;
if (a[j] >= temp)
break;
a[i] = a[j]; //把較小的子結點往上移動,替換它的父結點
i = j;
j = 2 * i + 1;
}
a[i] = temp;
}
//在最小堆中刪除數
void MinHeapDeleteNumber(int a[], int n)
{
Swap(a[0], a[n - 1]);
MinHeapFixdown(a, 0, n - 1);
}
//建立最小堆
void MakeMinHeap(int a[], int n)
{
for (int i = n / 2 - 1; i >= 0; i--)
MinHeapFixdown(a, i, n);
}
void MinheapsortTodescendarray(int a[], int n)
{
for (int i = n - 1; i >= 1; i--)
{
Swap(a[i], a[0]);
MinHeapFixdown(a, 0, i);
}
}4.時間複雜度:
最好情況:\(O\left ( N\log N\right )\)
最壞情況:\(O\left ( N\log N \right )\)
平均情況:\(O\left ( N\log N \right )\)
由於每次重新恢復堆的時間複雜度為\(O\left ( \log N \right )\),共N - 1次重新恢復堆操作,再加上前面建立堆時N / 2次向下調整,每次調整時間複雜度也為\(O\left ( \log N \right )\)。二次操作時間相加還是\(O\left ( N\log N \right )\)。故堆排序的時間複雜度為\(O\left ( N\log N \right )\)。
5.空間複雜度:
堆排序是就地排序,輔助空間為\(O\left (1 \right )\)。
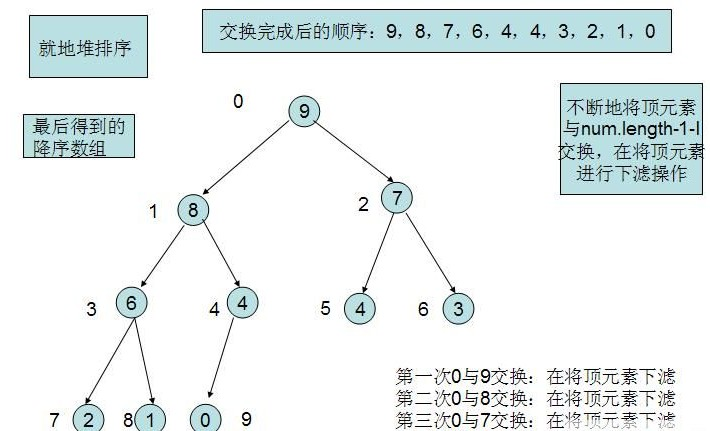
***
補:關於堆的幾個函式:(摘自MoreWindows大佬)
建立堆
make_heap(_First, _Last, _Comp)
預設是建立最大堆的。對int型別,可以在第三個引數傳入greater
在堆中新增資料
push_heap (_First, _Last)
要先在容器中加入資料,再呼叫push_heap ()
在堆中刪除資料
pop_heap(_First, _Last)
要先呼叫pop_heap()再在容器中刪除資料
堆排序
sort_heap(_First, _Last)
排序之後就不再是一個合法的heap了
二、 \(O\left ( N\right )\)
\(\left ( 1\right )\)桶排序(穩定)
1.原理:
(以下摘自百度)
假定:輸入是由一個隨機過程產生的[0, 1)區間上均勻分佈的實數。將區間[0, 1)劃分為n個大小相等的子區間(桶),每桶大小1/n:[0, 1/n), [1/n, 2/n), [2/n, 3/n),…,[k/n, (k+1)/n ),…將n個輸入元素分配到這些桶中,對桶中元素進行排序,然後依次連線桶輸入0 ≤A[1..n] <1輔助陣列B[0..n-1]是一指標陣列,指向桶(連結串列)。
樣例:
這裡有一個數列{6,8,7,4,2,5},最大值不超過10;
我們定義三個陣列,數列陣列(a【】),桶陣列(T【】),桶陣列編號(Tn【】)
\(\begin{array} {|c||c||c|} a& T & Tn \\ \\6&0&0 \\8&0&1 \\7&0&2 \\4&0&3 \\2&0&4 \\5&0&5 \\0&0&6 \\0&0&7 \\0&0&8 \\0&0&9 \end{array}\)
我們進行桶排序,這個過程類似這樣:空桶[ 待排陣列[ i ] ]++。
\(\begin{array} {|c||c||c|} a& T & Tn \\ \\6&0&0 \\8&1&1 \\7&0&2 \\4&1&3 \\2&1&4 \\5&1&5 \\0&1&6 \\0&1&7 \\0&0&8 \\0&0&9 \end{array}\)
若T[i]!=0,輸出其對應的Tn[i+1].
2.考點:桶排很多時候只是程式的一部分,他是一種思路,如P2119 魔法陣
3.關鍵程式碼:
①計數排序:(即普通桶排,所排陣列不超過int範圍)
for(int i=1;i<=N;i++)
{
T[a[i]]++;
}
for(int i=1,j=1;i<=M;i++)//M為a[]最大值
{
while((T[i]--)>0)
{
a[j++]=i;
}
}②離散化(所排陣列不在int範圍內)
STL庫map<>
map<LL,LL>T;
for(int i=1;i<=N;i++)
{
T[a[i]]++;
}
for(int i=1,j=1;i<=M;i++)//M為a[]最大值
{
while((T[i]--)>0)
{
a[j++]=i;
}
}4.時間複雜度:
\(O\left ( N\right )\),為線性排序,是排序中最快的。
5.空間複雜度:
\(O\left ( Maxn\right )\),其中\(Maxn\)為a【】中最大的數

總結:
排序演算法除了上述以外,還有基數排序(穩定,\(O\left ( N\right )\)),希爾排序(不穩定,\(O\left ( N^{1.25}\right )\)),直接插入排序(穩定,\(O\left ( N^2\right )\)),下面是一張排序演算法的時間複雜度表
| 排序方法 | 平均時間 | 最好時間 | 最壞時間 |
|---|---|---|---|
| 桶排序(穩定) | \(O\left ( N\right )\) | \(O\left ( N\right )\) | \(O\left ( N\right )\) |
| 基數排序(穩定) | \(O\left ( N\right )\) | \(O\left ( N\right )\) | \(O\left ( N\right )\) |
| 歸併排序(穩定) | \(O\left ( N\log N\right )\) | \(O\left ( N\log N\right )\) | \(O\left ( N\log N\right )\) |
| 快速排序(不穩定) | \(O\left ( N\log N\right )\) | \(O\left ( N\log N\right )\) | \(O\left ( N^2 \right )\) |
| 堆排序(不穩定) | \(O\left ( N\log N\right )\) | \(O\left ( N\log N\right )\) | \(O\left ( N\log N\right )\) |
| 希爾排序(不穩定) | \(O\left ( N^{1.25}\right )\) | ||
| 氣泡排序(穩定) | \(O\left ( N^2 \right )\) | \(O\left ( N\right )\) | \(O\left ( N^2 \right )\) |
| 選擇排序(不穩定) | \(O\left ( N^2 \right )\) | \(O\left ( N^2 \right )\) | \(O\left ( N^2 \right )\) |
| 直接插入排序(穩定) | \(O\left ( N^2 \right )\) | \(O\left ( N\right )\) | \(O\left ( N^2 \right )\) |
