複習一下吧, 排序演算法
阿新 • • 發佈:2018-11-25
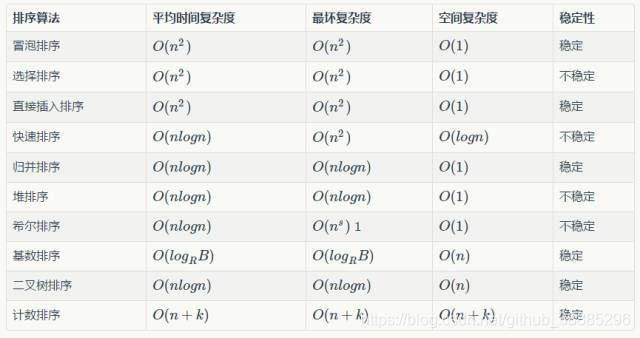
先來張圖片
氣泡排序
演算法描述
- <1>.比較相鄰的元素。如果第一個比第二個大,就交換它們兩個;
- <2>.對每一對相鄰元素作同樣的工作,從開始第一對到結尾的最後一對,這樣在最後的元素應該會是最大的數;
- <3>.針對所有的元素重複以上的步驟,除了最後一個;
- <4>.重複步驟1~3,直到排序完成。
程式碼實現
設定一標誌性變數pos,用於記錄每趟排序中最後一次進行交換的位置。由於pos位置之後的記錄均已交換到位,故在進行下一趟排序時只要掃描到pos位置即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
function bubbleSort(arr) {
var i = arr.length-1; //初始時,最後位置保持不變
while ( i> 0) {
var pos= 0; //每趟開始時,無記錄交換
for (var j= 0; j< i; j++)
if (arr[j]> arr[j+1]) {
pos= j; //記錄交換的位置
var tmp = arr[j]; arr[j]=arr[j+1];arr[j+1]=tmp;
}
i= pos; //為下一趟排序作準備
}
console.timeEnd('改進後氣泡排序耗時');
return arr;
}
|
選擇排序
演算法描述
- <1>.初始狀態:無序區為R[1..n],有序區為空;
- <2>.第i趟排序(i=1,2,3…n-1)開始時,當前有序區和無序區分別為R[1..i-1]和R(i..n)。該趟排序從當前無序區中-選出關鍵字最小的記錄 R[k],將它與無序區的第1個記錄R交換,使R[1..i]和R[i+1..n)分別變為記錄個數增加1個的新有序區和記錄個數減少1個的新無序區;
- <3>.n-1趟結束,陣列有序化了。
程式碼實現
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
function selectionSort(arr) {
var len = arr.length;
var minIndex, temp;
for (var i = 0; i < len - 1; i++) {
minIndex = i;
for (var j = i + 1; j < len; j++) {
if (arr[j] < arr[minIndex]) { //尋找最小的數
minIndex = j; //將最小數的索引儲存
}
}
temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
return arr;
}
|
插入排序
演算法描述
- <1>.從第一個元素開始,該元素可以認為已經被排序;
- <2>.取出下一個元素,在已經排序的元素序列中從後向前掃描;
- <3>.如果該元素(已排序)大於新元素,將該元素移到下一位置;
- <4>.重複步驟3,直到找到已排序的元素小於或者等於新元素的位置;
- <5>.將新元素插入到該位置後;
- <6>.重複步驟2~5。
程式碼描述
1 2 3 4 5 6 7 8 9 10 11 12 |
function insertionSort(array) {
for (var i = 1; i < array.length; i++) {
var key = array[i];
var j = i - 1;
while (j >= 0 && array[j] > key) {
array[j + 1] = array[j];
j--;
}
array[j + 1] = key;
}
return array;
}
|
演算法分析
- 最佳情況:輸入陣列按升序排列。T(n) = O(n)
- 最壞情況:輸入陣列按降序排列。T(n) = O(n2)
- 平均情況:T(n) = O(n2)
希爾排序
演算法描述
- <1>. 選擇一個增量序列t1,t2,…,tk,其中ti>tj,tk=1;
- <2>.按增量序列個數k,對序列進行k 趟排序;
- <3>.每趟排序,根據對應的增量ti,將待排序列分割成若干長度為m 的子序列,分別對各子表進行直接插入排序。僅增量因子為1 時,整個序列作為一個表來處理,表長度即為整個序列的長度。
程式碼實現
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
function shellSort(arr) {
var len = arr.length,
temp,
gap = 1;
console.time('希爾排序耗時:');
while(gap < len/5) { //動態定義間隔序列
gap =gap*5+1;
}
for (gap; gap > 0; gap = Math.floor(gap/5)) {
for (var i = gap; i < len; i++) {
temp = arr[i];
for (var j = i-gap; j >= 0 && arr[j] > temp; j-=gap) {
arr[j+gap] = arr[j];
}
arr[j+gap] = temp;
}
}
console.timeEnd('希爾排序耗時:');
return arr;
}
|
演算法分析
- 最佳情況:T(n) = O(nlog2 n)
- 最壞情況:T(n) = O(nlog2 n)
- 平均情況:T(n) =O(nlog n)
歸併排序
演算法描述
- <1>把長度為n的輸入序列分成兩個長度為n/2的子序列;
- <2>對這兩個子序列分別採用歸併排序;
- <3>將兩個排序好的子序列合併成一個最終的排序序列。
程式碼實現
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
function mergeSort(arr) { //採用自上而下的遞迴方法
var len = arr.length;
if(len < 2) {
return arr;
}
var middle = Math.floor(len / 2),
left = arr.slice(0, middle),
right = arr.slice(middle);
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right)
{
var result = [];
console.time('歸併排序耗時');
while (left.length && right.length) {
if (left[0] <= right[0]) {
result.push(left.shift());
} else {
result.push(right.shift());
}
}
while (left.length)
result.push(left.shift());
while (right.length)
result.push(right.shift());
console.timeEnd('歸併排序耗時');
return result;
}
|
演算法分析
- 最佳情況:T(n) = O(n)
- 最壞情況:T(n) = O(nlog n)
- 平均情況:T(n) =O(nlog n)
快速排序
演算法描述
- <1>從數列中挑出一個元素,稱為 “基準”(pivot);
- <2>重新排序數列,所有元素比基準值小的擺放在基準前面,所有元素比基準值大的擺在基準的後面(相同的數可以到任一邊)。在這個分割槽退出之後,該基準就處於數列的中間位置。這個稱為分割槽(partition)操作;
- <3>遞迴地(recursive)把小於基準值元素的子數列和大於基準值元素的子數列排序。
程式碼實現
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
var arr = [12,3,23,5,17,9,15,46];
function quickSort(arr,left, right){
var i,j,t,temp;
if(left>right){
return;
}
i = left;
j = right;
temp = arr[left];
while(i!==j){
while(temp<=arr[j]&&i<j){
j--;
}
while(temp>=arr[i]&&i<j){
i++
}
if(i<j){
[arr[j], arr[i]] = [arr[i], arr[j]];
}
}
arr[left] = arr[i];
arr[i] = temp;
quickSort(arr,left,i-1);
quickSort(arr,i+1,right);
}
quickSort(arr,0, arr.length-1);
console.log(arr);
|
演算法分析
- 最佳情況:T(n) = O(nlogn)
- 最壞情況:T(n) = O(n2)
- 平均情況:T(n) =O(nlog n)
堆排序
演算法描述
- <1>將初始待排序關鍵字序列(R1,R2….Rn)構建成大頂堆,此堆為初始的無序區;
- <2>將堆頂元素R[1]與最後一個元素R[n]交換,此時得到新的無序區(R1,R2,……Rn-1)和新的有序區(Rn),且滿足R[1,2…n-1]<=R[n];
- <3>由於交換後新的堆頂R[1]可能違反堆的性質,因此需要對當前無序區(R1,R2,……Rn-1)調整為新堆,然後再次將R[1]與無序區最後一個元素交換,得到新的無序區(R1,R2….Rn-2)和新的有序區(Rn-1,Rn)。不斷重複此過程直到有序區的元素個數為n-1,則整個排序過程完成。
程式碼實現
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
function heapify(arr, x, len) { if (Object.prototype.toString.call(arr).slice(8, -1) === 'Array' && typeof x === 'number') { var l = 2 * x + 1, r = 2 * x + 2, largest = x, temp; if (l < len && arr[l] > arr[largest]) { largest = l; } if (r < len && arr[r] > arr[largest]) { largest = r; } if (largest != x) { temp = arr[x]; arr[x] = arr[largest]; arr[largest] = temp; heapify(arr, largest, len); } } else { return 'arr is not an Array or x is not a number!'; } } /*方法說明:維護堆的性質 @param arr 陣列 @param x 陣列下標 @param len 堆大小*/ function heapify(arr, x, len) { if (Object.prototype.toString.call(arr).slice(8, -1) === 'Array' && typeof x === 'number') { var l = 2 * x + 1, r = 2 * x + 2, largest = x, temp; if (l < len && arr[l] > arr[largest]) { largest = l; } if (r < len && arr[r] > arr[largest]) { largest = r; } if (largest != x) { temp = arr[x]; arr[x] = arr[largest]; arr[largest] = temp; heapify(arr, largest, len); } } else { return 'arr is not an Array or x is not a number!'; } }
演算法分析
- 最佳情況:T(n) = O(nlogn)
- 最壞情況:T(n) = O(nlogn)
- 平均情況:T(n) =O(nlogn)
