如何理解 Graph Convolutional Network（GCN）？

阿新 • • 發佈：2018-11-28

作者：superbrother
連結：https://www.zhihu.com/question/54504471/answer/332657604
來源：知乎
著作權歸作者所有。商業轉載請聯絡作者獲得授權，非商業轉載請註明出處。

從CNN到GCN的聯絡與區別——GCN從入門到精（fang）通（qi）

1 什麼是離散卷積？CNN中卷積發揮什麼作用？

瞭解GCN之前必須對離散卷積（或者說CNN中的卷積）有一個明確的認識：

如何通俗易懂地解釋卷積？這個連結的內容已經講得很清楚了，離散卷積本質就是一種加權求和。

如圖1所示，CNN中的卷積本質上就是利用一個共享引數的過濾器（kernel），通過計算中心畫素點以及相鄰畫素點的加權和來構成feature map實現空間特徵的提取

，當然加權係數就是卷積核的權重係數。

那麼卷積核的係數如何確定的呢？是隨機化初值，然後根據誤差函式通過反向傳播梯度下降進行迭代優化。這是一個關鍵點，卷積核的引數通過優化求出才能實現特徵提取的作用，GCN的理論很大一部分工作就是為了引入可以優化的卷積引數。

圖1 CNN中卷積提取feature map示意圖

2 GCN中的Graph指什麼？為什麼要研究GCN？

CNN是Computer Vision裡的大法寶，效果為什麼好呢？原因在上面已經分析過了，可以很有效地提取空間特徵。但是有一點需要注意：CNN處理的影象或者視訊資料中畫素點（pixel）是排列成成很整齊的矩陣（如圖2所示，也就是很多論文中所提到的Euclidean Structure）。

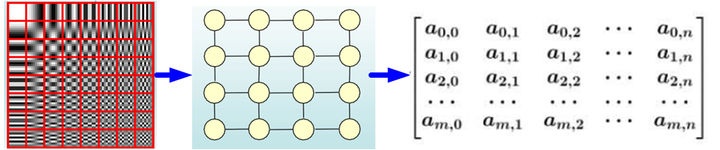
圖2 影象矩陣示意圖（Euclidean Structure）

與之相對應，科學研究中還有很多Non Euclidean Structure的資料，如圖3所示。社交網路、資訊網路中有很多類似的結構。

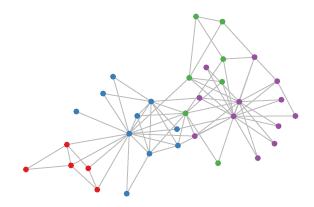
圖3 社交網路拓撲示意（Non Euclidean Structure）

實際上，這樣的網路結構（Non Euclidean Structure）就是圖論中抽象意義上的拓撲圖。

所以，Graph Convolutional Network中的Graph是指數學（圖論）中的用頂點和邊建立相應關係的拓撲圖。

那麼為什麼要研究GCN？原因有三：

(1)CNN無法處理Non Euclidean Structure的資料，學術上的表達是傳統的離散卷積（如問題1中所述）在Non Euclidean Structure的資料上無法保持平移不變性

。通俗理解就是在拓撲圖中每個頂點的相鄰頂點數目都可能不同，那麼當然無法用一個同樣尺寸的卷積核來進行卷積運算。

(2)由於CNN無法處理Non Euclidean Structure的資料，又希望在這樣的資料結構（拓撲圖）上有效地提取空間特徵來進行機器學習，所以GCN成為了研究的重點。

(3)讀到這裡大家可能會想，自己的研究問題中沒有拓撲結構的網路，那是不是根本就不會用到GCN呢？其實不然，廣義上來講任何資料在賦範空間內都可以建立拓撲關聯，譜聚類就是應用了這樣的思想（譜聚類（spectral clustering）原理總結）。所以說拓撲連線是一種廣義的資料結構，GCN有很大的應用空間。

綜上所述，GCN是要為除CV、NLP之外的任務提供一種處理、研究的模型。

3 提取拓撲圖空間特徵的兩種方式

GCN的本質目的就是用來提取拓撲圖的空間特徵，那麼實現這個目標只有graph convolution這一種途徑嗎？當然不是，在vertex domain(spatial domain)和spectral domain實現目標是兩種最主流的方式。

(1)vertex domain(spatial domain)是非常直觀的一種方式。顧名思義：提取拓撲圖上的空間特徵，那麼就把每個頂點相鄰的neighbors找出來。這裡面蘊含的科學問題有二：

a.按照什麼條件去找中心vertex的neighbors，也就是如何確定receptive field？

b.確定receptive field，按照什麼方式處理包含不同數目neighbors的特徵？

根據a,b兩個問題設計演算法，就可以實現目標了。推薦閱讀這篇文章Learning Convolutional Neural Networks for Graphs（圖4是其中一張圖片，可以看出大致的思路）。

圖4 vertex domain提取空間特徵示意

這種方法主要的缺點如下：

c.每個頂點提取出來的neighbors不同，使得計算處理必須針對每個頂點

d.提取特徵的效果可能沒有卷積好

當然，對這個思路喜歡的讀者可以繼續搜尋相關文獻，學術的魅力在於百家爭鳴嘛！

(2)spectral domain就是GCN的理論基礎了。這種思路就是希望藉助圖譜的理論來實現拓撲圖上的卷積操作。從整個研究的時間程序來看：首先研究GSP（graph signal processing）的學者定義了graph上的Fourier Transformation，進而定義了graph上的convolution，最後與深度學習結合提出了Graph Convolutional Network。

認真讀到這裡，腦海中應該會浮現出一系列問題：

Q1 什麼是Spectral graph theory？

Spectral graph theory請參考這個，簡單的概括就是藉助於圖的拉普拉斯矩陣的特徵值和特徵向量來研究圖的性質

Q2 GCN為什麼要利用Spectral graph theory？

這應該是看論文過程中讀不懂的核心問題了，要理解這個問題需要大量的數學定義及推導，沒有一定的數學功底難以駕馭（我也才疏學淺，很難回答好這個問題）。

所以，先繞過這個問題，來看Spectral graph實現了什麼，再進行探究為什麼？

4 什麼是拉普拉斯矩陣？為什麼GCN要用拉普拉斯矩陣？

Graph Fourier Transformation及Graph Convolution的定義都用到圖的拉普拉斯矩陣，那麼首先來介紹一下拉普拉斯矩陣。

對於圖 $G=(V,E)$ ，其Laplacian 矩陣的定義為 $L=D-A$ ，其中 $L$ 是Laplacian 矩陣， $D$ 是頂點的度矩陣（對角矩陣），對角線上元素依次為各個頂點的度， $A$ 是圖的鄰接矩陣。看圖5的示例，就能很快知道Laplacian 矩陣的計算方法。

圖5 Laplacian 矩陣的計算方法

這裡要說明的是：常用的拉普拉斯矩陣實際有三種：

No.1 $L=D-A$ 定義的Laplacian 矩陣更專業的名稱叫Combinatorial Laplacian

No.2 $L^{sys}=D^{-1/2}LD^{-1/2}$ 定義的叫Symmetric normalized Laplacian，很多GCN的論文中應用的是這種拉普拉斯矩陣

No.3 $L^{rw}=D^{-1}L$ 定義的叫Random walk normalized Laplacian,有讀者的留言說看到了Graph Convolution與Diffusion相似之處，當然從Random walk normalized Laplacian就能看出了兩者確有相似之處（其實兩者只差一個相似矩陣的變換，可以參考Diffusion-Convolutional Neural Networks，以及下圖）

不需要相關內容的讀者可以略過此部分

Diffusion Graph Convolution與Spectral Graph Convolution相似性證明

其實維基本科對Laplacian matrix的定義上寫得很清楚，國內的一些介紹中只有第一種定義。這讓我在最初看文獻的過程中感到一些的困惑，特意寫下來，幫助大家避免再遇到類似的問題。

為什麼GCN要用拉普拉斯矩陣？

拉普拉斯矩陣矩陣有很多良好的性質，這裡寫三點我感觸到的和GCN有關之處

(1)拉普拉斯矩陣是對稱矩陣，可以進行特徵分解（譜分解），這就和GCN的spectral domain對應上了

(2)拉普拉斯矩陣只在中心頂點和一階相連的頂點上（1-hop neighbor）有非0元素，其餘之處均為0

（3）通過拉普拉斯運算元與拉普拉斯矩陣進行類比（詳見第6節）

以上三點是我的一些理解，當然嚴格意義上，拉普拉斯矩陣應用於GCN有嚴謹的數學推導與證明。

5 拉普拉斯矩陣的譜分解（特徵分解）

GCN的核心基於拉普拉斯矩陣的譜分解，文獻中對於這部分內容沒有講解太多，初學者可能會遇到不少誤區，所以先了解一下特徵分解。

矩陣的譜分解，特徵分解，對角化都是同一個概念（特徵分解_百度百科）。

不是所有的矩陣都可以特徵分解，其充要條件為n階方陣存在n個線性無關的特徵向量。

但是拉普拉斯矩陣是半正定對稱矩陣（半正定矩陣本身就是對稱矩陣，半正定矩陣_百度百科，此處這樣寫為了和下面的性質對應，避免混淆），有如下三個性質：

對稱矩陣一定n個線性無關的特徵向量
半正定矩陣的特徵值一定非負
對陣矩陣的特徵向量相互正交，即所有特徵向量構成的矩陣為正交矩陣。

由上可以知道拉普拉斯矩陣一定可以譜分解，且分解後有特殊的形式。

對於拉普拉斯矩陣其譜分解為：

$L= U\left(\begin{matrix}\lambda_1 & \\&\ddots \\ &&\lambda_n \end{matrix}\right) U^{-1}$

其中 $U=(\vec{u_1},\vec{u_2},\cdots,\vec{u_n})$ ，是列向量為單位特徵向量的矩陣，也就說 $\vec{u_l}$ 是列向量。

$\left(\begin{matrix}\lambda_1 & \\&\ddots \\ &&\lambda_n \end{matrix}\right)$ 是n個特徵值構成的對角陣。

由於 $U$ 是正交矩陣，即 $UU^{T}=E$

所以特徵分解又可以寫成：

$L= U\left(\begin{matrix}\lambda_1 & \\&\ddots \\ &&\lambda_n \end{matrix}\right) U^{T}$

文獻中都是最後匯出的這個公式，但大家不要誤解，特徵分解最右邊的是特徵矩陣的逆，只是拉普拉斯矩陣的性質才可以寫成特徵矩陣的轉置。

其實從上可以看出：整個推導用到了很多數學的性質，在這裡寫得詳細一些，避免大家形成錯誤的理解。

6 如何從傳統的傅立葉變換、卷積類比到Graph上的傅立葉變換及卷積？

把傳統的傅立葉變換以及卷積遷移到Graph上來，核心工作其實就是把拉普拉斯運算元的特徵函式 $e^{-i\omega t}$ 變為Graph對應的拉普拉斯矩陣的特徵向量。

(1)推廣傅立葉變換

想親自躬行的讀者可以閱讀The Emerging Field of Signal Processing on Graphs: Extending High-Dimensional Data Analysis to Networks and Other Irregular Domains這篇論文，下面是我的理解與提煉：

(a)Graph上的傅立葉變換

傳統的傅立葉變換定義為：

$F(\omega)=\mathcal{F}[f(t)]=\int_{}^{}f(t)e^{-i\omega t} dt$

訊號 $f(t)$ 與基函式 $e^{-i\omega t}$ 的積分，那麼為什麼要找 $e^{-i\omega t}$ 作為基函式呢？從數學上看， $e^{-i\omega t}$ 是拉普拉斯運算元的特徵函式（滿足特徵方程）, $\omega$ 就和特徵值有關。

廣義的特徵方程定義為：

$A V=\lambda V$

其中 $A$ 是一種變換， $V$ 是特徵向量或者特徵函式（無窮維的向量）， $\lambda$ 是特徵值。

$e^{-i\omega t}$ 滿足：

$\Delta e^{-i\omega t}=\frac{\partial^{2}}{\partial t^{2}} e^{-i\omega t}=-\omega^{2} e^{-i\omega t}\$

當然 $e^{-i\omega t}$ 就是變換 $\Delta$ 的特徵函式， $\omega$ 和特徵值密切相關。

那麼，可以聯想了，處理Graph問題的時候，用到拉普拉斯矩陣（拉普拉斯矩陣就是離散拉普拉斯運算元，想了解更多可以參考Discrete Laplace operator），自然就去找拉普拉斯矩陣的特徵向量了。

$L$ 是拉普拉斯矩陣， $V$ 是其特徵向量，自然滿足下式

$LV=\lambda V$

離散積分就是一種內積形式，仿上定義Graph上的傅立葉變換：

$F(\lambda_l)=\hat{f}(\lambda_l)=\sum_{i=1}^{N}{f(i) u_l^*(i)}$

$f$ 是Graph上的 $N$ 維向量， $f(i)$ 與Graph的頂點一一對應， $u_l(i)$ 表示第 $l$ 個特徵向量的第 $i$ 個分量。那麼特徵值（頻率） $\lambda_l$ 下的， $f$ 的Graph 傅立葉變換就是與 $\lambda_l$ 對應的特徵向量 $u_l$ 進行內積運算。

注：上述的內積運算是在複數空間中定義的，所以採用了 $u_l^*(i)$ ，也就是特徵向量 $u_l$ 的共軛。Inner product更多可以參考Inner product space。

利用矩陣乘法將Graph上的傅立葉變換推廣到矩陣形式：

$\left(\begin{matrix} \hat{f}(\lambda_1)\\ \hat{f}(\lambda_2) \\ \vdots \\\hat{f}(\lambda_N) \end{matrix}\right)=\left(\begin{matrix}\ u_1(1) &u_1(2)& \dots &u_1(N) \\u_2(1) &u_2(2)& \dots &u_2(N)\\ \vdots &\vdots &\ddots & \vdots\\ u_N(1) &u_N(2)& \dots &u_N(N) \end{matrix}\right)\left(\begin{matrix}f(1)\\ f(2) \\ \vdots \\f(N) \end{matrix}\right)$

即 $f$ 在Graph上傅立葉變換的矩陣形式為： $\hat{f}=U^Tf \qquad(a)$

式中： $U^T$ 的定義與第五節中的相同

(b)Graph上的傅立葉逆變換

類似地，傳統的傅立葉變換是對頻率 $\omega$ 求積分：

$\mathcal{F}^{-1}[F(\omega)]=\frac{1}{2\Pi}\int_{}^{}F(\omega)e^{i\omega t} d\omega$

遷移到Graph上變為對特徵值 $\lambda_l$ 求和：

$f(i)=\sum_{l=1}^{N}{\hat{f}(\lambda_l) u_l(i)}$

利用矩陣乘法將Graph上的傅立葉逆變換推廣到矩陣形式：

$\left(\begin{matrix}f(1)\\ f(2) \\ \vdots \\f(N) \end{matrix}\right)= \left(\begin{matrix}\ u_1(1) &u_2(1)& \dots &u_N(1) \\u_1(2) &u_1(2)& \dots &u_N(2)\\ \vdots &\vdots &\ddots & \vdots\\ u_1(N) &u_2(N)& \dots &u_N(N) \end{matrix}\right) \left(\begin{matrix} \hat{f}(\lambda_1)\\ \hat{f}(\lambda_2) \\ \vdots \\\hat{f}(\lambda_N) \end{matrix}\right)$

即 $f$ 在Graph上傅立葉逆變換的矩陣形式為： $f=U\hat{f} \qquad(b)$

式中： $U$ 的定義與第五節中的相同

(2)推廣卷積

在上面的基礎上，利用卷積定理類比來將卷積運算，推廣到Graph上。

卷積定理：函式卷積的傅立葉變換是函式傅立葉變換的乘積，即對於函式 $f(t)$ 與 $h(t)$ 兩者的卷積是其函式傅立葉變換乘積的逆變換：

$f*h=\mathcal{F}^{-1}\left[ \hat{f}(\omega)\hat{h}(\omega) \right]=\frac{1}{2\Pi}\int_{}^{} \hat{f}(\omega)\hat{h}(\omega)e^{i\omega t} d\omega$

類比到Graph上並把傅立葉變換的定義帶入， $f$ 與卷積核 $h$ 在Graph上的卷積可按下列步驟求出：

$f$ 的傅立葉變換為 $\hat{f}=U^Tf$

卷積核 $h$ 的傅立葉變換寫成對角矩陣的形式即為： $\left(\begin{matrix}\hat h(\lambda_1) & \\&\ddots \\ &&\hat h(\lambda_n) \end{matrix}\right)$

$\hat{h}(\lambda_l)=\sum_{i=1}^{N}{h(i) u_l^*(i)}$ 是根據需要設計的卷積核 $h$ 在Graph上的傅立葉變換。

兩者的傅立葉變換乘積即為： $\left(\begin{matrix}\hat h(\lambda_1) & \\&\ddots \\ &&\hat h(\lambda_n) \end{matrix}\right)U^Tf$

再乘以 $U$ 求兩者傅立葉變換乘積的逆變換，則求出卷積：

$(f*h)_G= U\left(\begin{matrix}\hat h(\lambda_1) & \\&\ddots \\ &&\hat h(\lambda_n) \end{matrix}\right) U^Tf \qquad(1)$

式中： $U$ 及 $U^{T}$ 的定義與第五節中的相同

注：很多論文中的Graph卷積公式為：

$(f*h)_G=U((U^Th)\odot(U^Tf)) \qquad(2)$

$\odot$ 表示hadamard product（哈達馬積），對於兩個向量，就是進行內積運算；對於維度相同的兩個矩陣，就是對應元素的乘積運算。

其實式(2)與式(1)是完全相同的。

因為 $\left(\begin{matrix}\hat h(\lambda_1) & \\&\ddots \\ &&\hat h(\lambda_n) \end{matrix}\right)$ 與 $U^Th$ 都是 $h$ 在Graph上的傅立葉變換

而根據矩陣乘法的運算規則：對角矩陣 $\left(\begin{matrix}\hat h(\lambda_1) & \\&\ddots \\ &&\hat h(\lambda_n) \end{matrix}\right)$ 與 $U^Tf$ 的乘積和 $U^Th$ 與 $U^Tf$ 進行對應元素的乘積運算是完全相同的。

這裡主要推(1)式是為了和後面的deep learning相結合。

這部分理論也是我看了很久才想明白的，在此記錄下來，如果是想繼續探究理論的朋友，可以作為“入門小引”，畢竟理論還很深！對於喜歡實踐的朋友，也能初步瞭解理論基礎，也是“開卷有益”。

7 為什麼拉普拉斯矩陣的特徵向量可以作為傅立葉變換的基？特徵值表示頻率？

(1)為什麼拉普拉斯矩陣的特徵向量可以作為傅立葉變換的基？

傅立葉變換一個本質理解就是：把任意一個函式表示成了若干個正交函式（由sin,cos 構成）的線性組合。

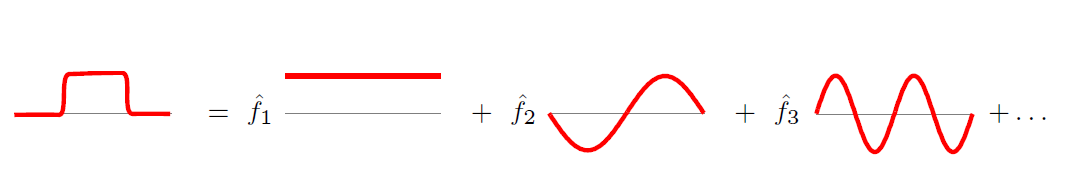
圖6 傅立葉逆變換圖示

通過第六節中(b)式也能看出，graph傅立葉變換也把graph上定義的任意向量 $f$ ，表示成了拉普拉斯矩陣特徵向量的線性組合，即：

$f=\hat{f}(1)u_1+\hat{f}(2)u_2+\cdots +\hat{f}(n)u_n$

那麼：為什麼graph上任意的向量 $f$ 都可以表示成這樣的線性組合？

原因在於 $(\vec{u_1},\vec{u_2},\cdots,\vec{u_n})$ 是graph上 $n$ 維空間中的 $n$ 個線性無關的正交向量（原因參看第五節中拉普拉斯矩陣的性質），由線性代數的知識可以知道： $n$ 維空間中 $n$ 個線性無關的向量可以構成空間的一組基，而且拉普拉斯矩陣的特徵向量還是一組正交基。

(2)怎麼理解拉普拉斯矩陣的特徵值表示頻率？

在graph空間上無法視覺化展示“頻率”這個概念，那麼從特徵方程上來抽象理解。

將拉普拉斯矩陣 $L$ 的 $n$ 個非負實特徵值，從小到大排列為 $\lambda_1 \le \lambda_2 \le \cdots \le \lambda_n$ ，而且最小的特徵值 $\lambda_1=0$ ，因為 $n$ 維的全1向量對應的特徵值為0（由 $L$ 的定義就可以得出）：

$L \left(\begin{matrix}1\\ 1 \\ \vdots \\1 \end{matrix}\right)=0$

從特徵方程的數學理解來看：

$Lu=\lambda u$

在由Graph確定的 $n$ 維空間中，越小的特徵值 $\lambda_l$ 表明：拉普拉斯矩陣 $L$ 其所對應的基 $u_l$ 上的分量、“資訊”越少，那麼當然就是可以忽略的低頻部分了。

其實影象壓縮就是這個原理，把畫素矩陣特徵分解後，把小的特徵值（低頻部分）全部變成0，PCA降維也是同樣的，把協方差矩陣特徵分解後，按從大到小取出前K個特徵值對應的特徵向量作為新的“座標軸”。

Graph Convolution的理論告一段落了，下面開始Graph Convolution Network

8 Deep Learning中的Graph Convolution

Deep learning 中的Graph Convolution直接看上去會和第6節推匯出的圖卷積公式有很大的不同，但是萬變不離其宗，(1)式是推導的本源。

第1節的內容已經解釋得很清楚：Deep learning 中的Convolution就是要設計含有trainable共享引數的kernel，從(1)式看很直觀：graph convolution中的卷積引數就是 $diag(\hat h(\lambda_l) )$ 。

第一代的GCN(Spectral Networks and Locally Connected Networks on Graphs)，簡單粗暴地把 $diag(\hat h(\lambda_l) )$ 變成了卷積核 $diag(\theta_l )$ ,也就是：

$y_{output}=\sigma \left(U\left(\begin{matrix}\theta_1 &\\&\ddots \\ &&\theta_n \end{matrix}\right) U^T x \right) \qquad(3)$

式（3）就是標準的第一代GCN中的layer了，其中 $\sigma(\cdot)$ 是啟用函式， $\Theta=({\theta_1},{\theta_2},\cdots,{\theta_n})$ 就跟三層神經網路中的weight一樣是任意的引數，通過初始化賦值然後利用誤差反向傳播進行調整， $x$ 就是graph上對應於每個頂點的特徵向量。

第一代的引數方法存在著一些弊端：主要在於：

（1）每一次前向傳播，都要計算 $U$ , $diag(\theta_l )$ 及 $U^T$ 三者的乘積，特別是對於大規模的graph，計算的代價較高，也就是論文中 $\mathcal{O}(n^2)$ 的計算複雜度

（2）卷積核的spatial localization不好，這是相對第二代卷積核而言的，這裡不多解釋

（3）卷積核需要 $n$ 個引數

由於以上的缺點第二代的卷積核設計應運而生。

第二代的GCN(Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering)，把 $\hat h(\lambda_l)$ 巧妙地設計成了 $\sum_{j=0}^K \alpha_j \lambda^j_l$ ，也就是：

$y_{output}=\sigma \left(U\left(\begin{matrix}\sum_{j=0}^K \alpha_j \lambda^j_1 &\\&\ddots \\ && \sum_{j=0}^K \alpha_j \lambda^j_n \end{matrix}\right) U^T x \right) \qquad(4)$

上面的公式彷彿還什麼都看不出來，下面利用矩陣乘法進行變換，來一探究竟。

$\left(\begin{matrix}\sum_{j=0}^K \alpha_j \lambda^j_1 &\\&\ddots \\ && \sum_{j=0}^K \alpha_j \lambda^j_n \end{matrix}\right)=\sum_{j=0}^K \alpha_j \Lambda^j$

進而可以匯出：

$U \sum_{j=0}^K \alpha_j \Lambda^j U^T =\sum_{j=0}^K \alpha_j U\Lambda^j U^T = \sum_{j=0}^K \alpha_j L^j$

上式成立是因為 $L^2=U \Lambda U^TU \Lambda U^T=U \Lambda^2 U^T$ 且 $U^T U=E$

各符號的定義都同第五節。

(4)式就變成了：

$y_{output}=\sigma \left( \sum_{j=0}^K \alpha_j L^j x \right) \qquad(5)$

其中 $({\alpha_1},{\alpha_2},\cdots,{\alpha_K})$ 是任意的引數，通過初始化賦值然後利用誤差反向傳播進行調整。

式(5)所設計的卷積核其優點在於在於：

（1）卷積核只有K個引數，一般 K遠小於n

（2）矩陣變換後，神奇地發現不需要做特徵分解了，直接用拉普拉斯矩陣 $L$ 進行變換，計算複雜度變成了 $\mathcal{O}(n)$

（3）卷積核具有很好的spatial localization，特別地，K就是卷積核的receptive field，也就是說每次卷積會將中心頂點K-hop neighbor上的feature進行加權求和，權係數就是 $\alpha_k$

更直觀地看， K=1就是對每個頂點上一階neighbor的feature進行加權求和，如下圖所示：

圖7 k=1 的graph convolution示意

同理，K=2的情形如下圖所示：

圖8 k=2 的graph convolution示意

注：上圖只是以一個頂點作為例項，GCN每一次卷積對所有的頂點都完成了圖示的操作。

如何理解 Graph Convolutional Network（GCN）？

1 什麼是離散卷積？CNN中卷積發揮什麼作用？

2 GCN中的Graph指什麼？為什麼要研究GCN？

3 提取拓撲圖空間特徵的兩種方式

4 什麼是拉普拉斯矩陣？為什麼GCN要用拉普拉斯矩陣？

5 拉普拉斯矩陣的譜分解（特徵分解）

6 如何從傳統的傅立葉變換、卷積類比到Graph上的傅立葉變換及卷積？

7 為什麼拉普拉斯矩陣的特徵向量可以作為傅立葉變換的基？特徵值表示頻率？

8 Deep Learning中的Graph Convolution

9 從數學的角度看Spectral Graph在GCN中的作用

如何理解 Graph Convolutional Network（GCN）？

graph attention network（ICLR2018）官方程式碼詳解（tensorflow）

圖卷積網路（Graph Convolutional Network）

CS229 6.17 Neurons Networks convolutional neural network（cnn）

Efficient Sub-Pixel Convolutional Neural Network（ESPCN）

關於Graph Convolutional Network的初步理解

《T-GCN: A Temporal Graph Convolutional Network for Trafﬁc Prediction》論文解讀

《T-GCN: A Temporal Graph Convolutional Network for Trafﬁc Prediction》程式碼解讀

2349 Arctic Network（中文版）

深入理解OkHttp源碼（一）——提交請求

深入理解Java：註解（Annotation）--註解處理器

深入理解Java的註解（Annotation）：註解處理器（3）

深入理解Flink核心技術（轉載）

javascript深入理解js閉包（轉）

深入理解Java虛擬機（筆記）

通俗易懂理解TCP和UDP（轉）

深入理解MyBatis的原理（三）：配置文件上

深入理解MyBatis的原理（三）：配置文件用法（續）

『中級篇』k8s基礎網絡Cluster Network（66）

從多個角度來理解協方差（covariance）

如何理解 Graph Convolutional Network（GCN）？

1 什麼是離散卷積？CNN中卷積發揮什麼作用？

2 GCN中的Graph指什麼？為什麼要研究GCN？

3 提取拓撲圖空間特徵的兩種方式

4 什麼是拉普拉斯矩陣？為什麼GCN要用拉普拉斯矩陣？

5 拉普拉斯矩陣的譜分解（特徵分解）

6 如何從傳統的傅立葉變換、卷積類比到Graph上的傅立葉變換及卷積？

7 為什麼拉普拉斯矩陣的特徵向量可以作為傅立葉變換的基？特徵值表示頻率？

8 Deep Learning中的Graph Convolution

9 從數學的角度看Spectral Graph在GCN中的作用

相關推薦