論文連結：https://arxiv.org/abs/1811.05320

最近發現部落格好像會被CSDN和一些奇怪的野雞網站爬下來？看見有人跟爬蟲機器人單方面討論問題我也蠻無奈的。總之原作者Missouter，部落格連結https://www.cnblogs.com/missouter/，歡迎交流。

整理、精煉了一下這篇論文的思路。

Abstract：

交通預測的難點在於交通拓撲網路複雜的結構與隨時間動態發生的交通變化；為了提取交通網的空間與時間特徵，文章提出了一種時間性的圖卷積網路模型，結合了門級迴圈單元（GRU）與圖卷積網路（GCN）。其中圖卷積網路被用於提取複雜拓撲結構中的空間性資訊，而門級迴圈單元則為了提取時間關係，被用於學習交通資料中的動態資料。

Introduction：

交通預測過程：分析交通道路狀況，包含流量、速度、密度；挖掘交通模式，同時對道路上的交通狀況進行預測。

預測結果：交通管理者預測擁堵狀況、限制交通工具的科學基礎、出行者效率選擇出行工具、路線的保障。

難點：

1、 空間關係：交通流的變化被拓撲結構的城市交通網主導，上游的交通狀態通過傳輸作用影響下游的交通狀態，而下游交通狀態通過反饋作用再影響上游交通。

2、 時間關係：交通流隨時間動態變化，主要表現在週期性和趨勢上；現有的交通狀況被前一刻的交通狀況影響。

現存交通預測方法缺陷：一些交通預測方法（ARIMA、Kalman filtering model，etc）只關注了交通狀況的動態變化而忽視了空間關係，導致交通狀態的變化不被道路網約束，同時一些模型嘗試使用卷積神經網路進行空間性建模，但這些模型一般只使用於歐幾里得型別的資料（規則矩陣、影象等），無法在拓撲結構的城市交通網路中運作。

T-GCN貢獻：

1、 結合了GCN與GRU，內容與abstract重複，不做多提。

2、 T-GCN的預測結果展示了一個不同視角下的穩定狀態，表示T-GCN除了預測短週期的變化，還能預測長週期的變化。

3、 我們使用兩個現實的資料集評估模型，相較其他預測模型，減少了1.5%~57.8%的預測錯誤率。

Related work：

交通預測方法分類：模型驅動的方法、資料驅動的方法；

模型驅動的方法：解釋即時、穩定的交通關係如交通流量、速度與密度，需要複雜細緻的系統建模與巨大的算力，且由於諸多因素的影響，現實環境中交通資料的多樣性無法被精確描繪。

資料驅動的方法：基於資料統計所得規律推斷交通狀況的變化。不分析物理屬性與交通系統的動態變化有著較高的複雜度。其中的historical average model不需要假設、計算過程簡單，但精確度不佳。

擁有更高精確度的模型被提出，分為兩種：含引數的與非引數的。

含參模型假定迴歸函式，引數在對原始資料的處理過程中確定。傳統含參的模型是在系統模型為靜態的假設基礎上建立的，反映不了交通系統的非線性與不確定性，也克服不了交通事故等突發隨機事件的困難。不含引數的模型只需要足夠的歷史資料就能自動學習靜態規律特徵，但先前形如LSTM、GRU的模型僅僅考慮了時間關係而忽略了空間關係，不能精確預測道路上的交通訊息，如何充分利用空間資訊成了交通預測的關鍵，而利用CNN進行空間關係提取的模型雖然在交通預測上取得了顯著進步，但無法應用於複雜拓撲結構的城市交通網，隨著GCN研究的深入，拓撲結構空間特徵的提取問題也得到解決。

（這段論文寫的有點長…堆了一堆文字讀的我有點難受）

Methodology:

問題定義：根據歷史資料預測某一特定時間段的交通訊息，交通資料通常被定義為速度、密集程度、交通流。使實驗不失普遍性，在實驗章節使用交通速度作為交通資料的代表。（Without loss of generality, we use traffic speed as an example of traffic information in experiment section.這句語感有點僵了）

定義：設定無權圖G=(V, E），V、E分別代表道路點與邊，N為道路的數量，設定鄰接N*N矩陣A表達道路與道路之間的聯絡；設定N*P特徵矩陣X，P代表點屬性特徵的數量，即歷史時間序列的長度，使用N*i矩陣 表示在時刻i，每條道路上的速度，屬性特徵也可以是交通速度、交通流等屬性。

問題轉化：交通空間-時間性預測被轉化為學習以拓撲圖G為前置與特徵矩陣X的對映函式，計算得到在下T時刻的交通訊息：

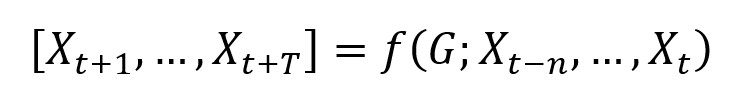
過程概覽：首先以長度為n的歷史時間序列資料作為輸入，使用GCN接收拓撲結構的空間資訊，其次將接收到的空間、時間資訊輸入GRU當中，獲取各個單元間的動態資訊變化，以提取時間性的特徵，最後在全連線層獲得結果。

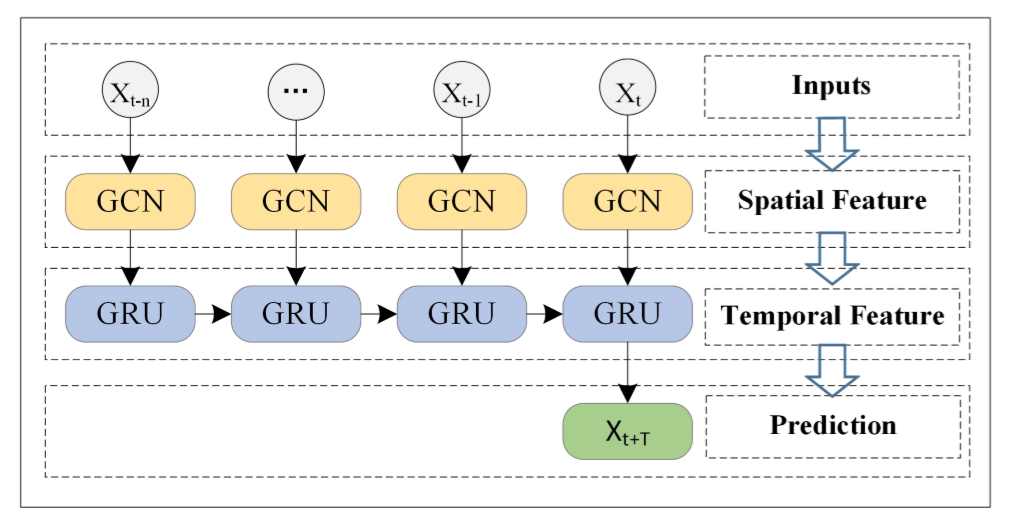
空間關係建模：利用GCN提取圖結構的資料，通過給定的鄰接矩陣A、特徵矩陣X，GCN在圖上通過提取相鄰結點特徵構建傅立葉域，使用堆疊的卷積網路，表示為：

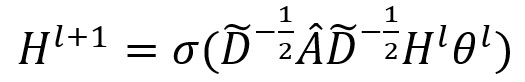
Â為A與單位矩陣I相加所得， D為度矩陣， H^l為第l層的輸出， θ^l包含該層的引數， σ代表非線性迴歸的啟用函式。(我懷疑論文這裡的上標打錯了)

兩層GCN模型可被表示為：

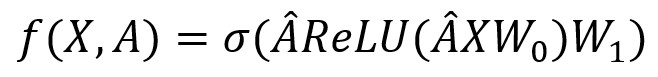
其中 ，P*H的 矩陣代表從輸入到隱藏層的權重，P為特徵矩陣的長度，H為隱藏單元的數量；H*T的W₁代表從隱藏層到輸出層的權重， f(X,A)∈R^N*T代表長度為T的預測輸出，ReLU()作為修正線性單元，作啟用層用。

時間關係建模：被廣泛應用的迴圈神經網路因梯度消失/爆炸的原因，不適用於長週期的預測；LSTM與GRU作為迴圈神經網路的變種，克服了上述問題。其共同原理都是利用門級機制儲存儘可能長的週期資訊；LSTM因其複雜的結構，GRU結構更加簡單，故計算時間更短。

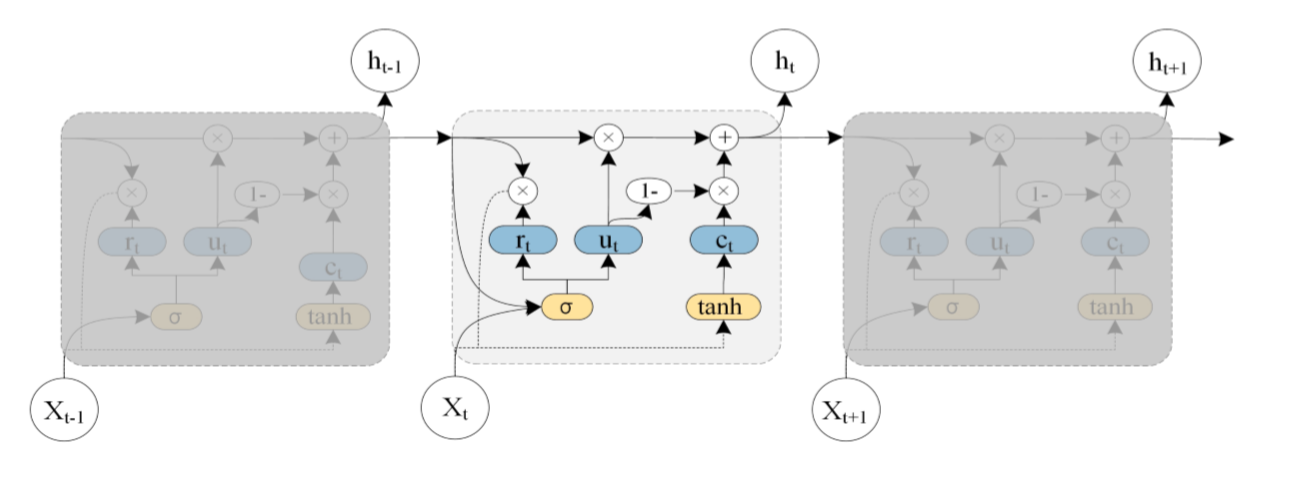
圖中h_t-1表示t-1時刻的隱藏狀態， x_t表示t時刻的交通訊息， r_t代表重置門，用於控制先前時刻狀態資訊的度量； u_t為上傳門，用於控制上傳到下一狀態的資訊度量； c_t為t時刻時儲存的資訊， h_t為t時刻的輸出狀態；總的來說，GRU通過獲取t-1時刻的隱藏狀態與當時的交通狀態資訊得到t時刻的交通訊息。

T-GCN：

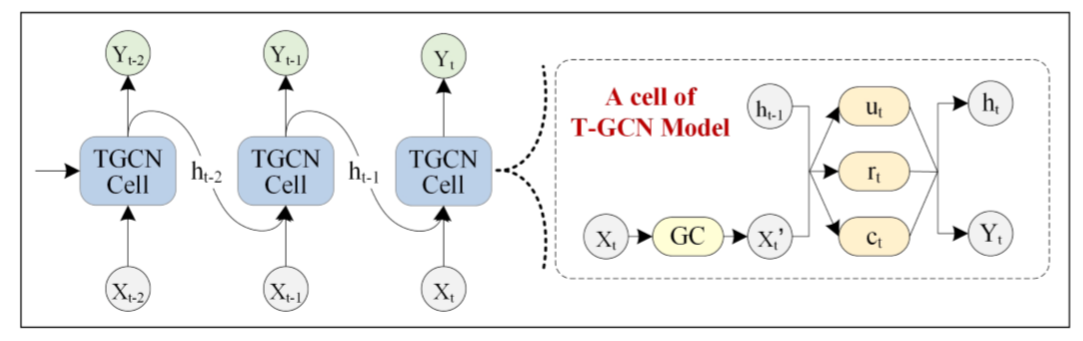
T-GCN的結構如圖，右側為T-GCN的處理單元： 為t-1時刻的輸出，GC為圖卷積過程，u_t 、 r_t分別為上傳門與重置門， 為t時刻的輸出。具體計算過程為：

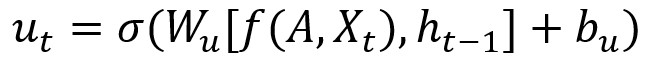
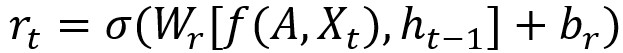
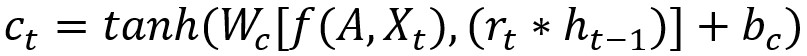
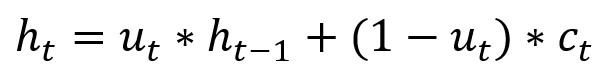
f(A,X)代表前文定義的GCN計算過程，w與b代表訓練過程中的權重與偏移量。（很大部分照搬了GNU的公式）

損失函式：

目標：最小化真實交通速度與預測交通速度的誤差。Y分別代表真實速度與預測速度，損失函式如下：

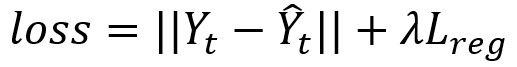
其中 λL_reg用於防止過擬合。

Experiments:

選取資料集：

1、SZ-taxi：資料分為兩部分，156*156的鄰接矩陣表示路與路之間的空間關係，描述每條路上隨時間變化的特徵矩陣。

2、Losloop：由鄰接矩陣與特徵矩陣組成，鄰接矩陣由交通網路中的感測器計算；同時作者對資料集中的殘缺部分使用線性填充的方法進行了補全。

輸入的資料全部進行了歸一化處理，80%的資料用於訓練，而20%的資料被用於測試。實驗對接下來15、30、45、60分鐘的交通速度進行預測。

評價指標：

文章列出了五個用於評價T-GCN預測表現的指標：

1、均方根誤差：

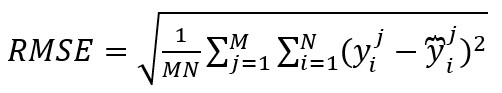
2、平均絕對誤差：

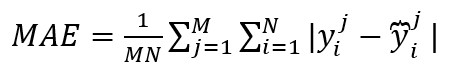
3、準確率：

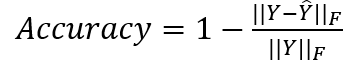
4、 確定係數：

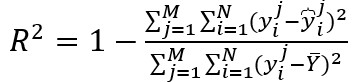
5、可釋方差值：

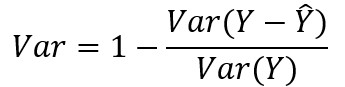
其中y^j'_i分別代表第j次時間、第i條路的真實交通訊息與預測資訊，M為時間樣本的數量，N為路的數量，Y分別代表 與 的集合， 帶上劃線的Y為Y的平均數。

R²與var用於計算相關係數，衡量預測結果表示實際資料的能力，數值越大則預測能力越優越。

選取模型引數：

超引數：包括學習率（0.001）、抓取數量（32）、訓練輪數（5000）、隱藏單元數量（通過多次實驗取最優預測效果）

針對SZ-taxi文章選取[8,16,32,64,100,128]，分析預測準確率的變化，得到不同隱藏單元數量下RASE與MAE、Accuracy、R² 、var的值如圖：

顯然數量為100時效果是最好的（真有這麼巧的事情嘛…）。隱藏單元超過一定數量效能下降的原因在於資料單元超過一定值後計算複雜度增加，且訓練資料會出現過擬合現象。

實驗結果：

將T-GCN預測效果與baseline對比，包括HA、ARIMA、SVR、GCN、GRU，所得實驗資料如下：

高預測精準度：門級迴圈網路的預測精度顯著高於其他baseline演算法，HA、ARIMA、SVR等演算法因難以處理複雜、非固定的時間資料而預測效果不佳，GCN預測效果不佳的原因僅僅在於僅考慮了空間特徵而忽略了交通資料是一個典型的時間序列資料這一事實。

ARIMA比HA檢測效果弱的原因在於ARIMA不適用於長週期的檢測，且計算每個節點誤差的方式導致一些資料中的波動會導致最終的計算錯誤。

時空預測能力：為了檢驗模型是否能夠從交通資料中提取時空特徵，文章將模型與GCN、GNU模型進行了比較：

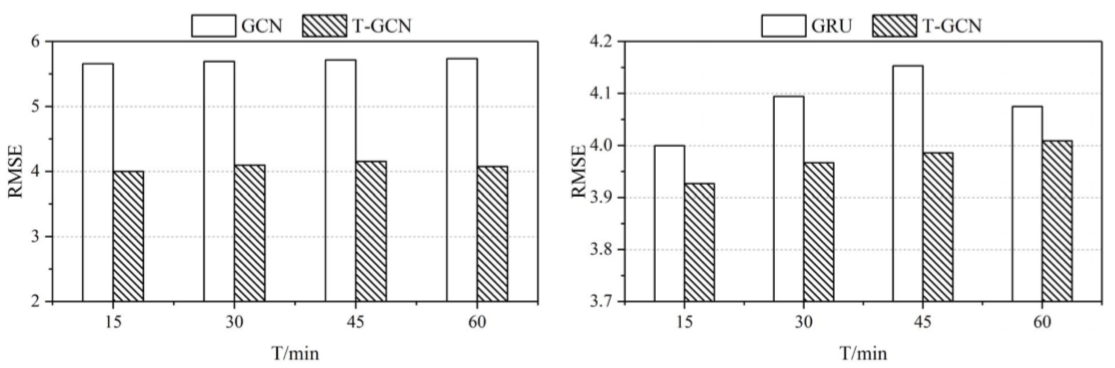
長週期預測能力：在不同的時間範圍（文章只寫了“horizon”，根據前後文認定為是時間範圍）下，T-GCN都能獲得最好的預測效果且預測結果擁有較小的變化趨勢，證明了T-GCN擁有更好的長週期預測能力；文章以T-GCN在不同時間點的結果作為論證：

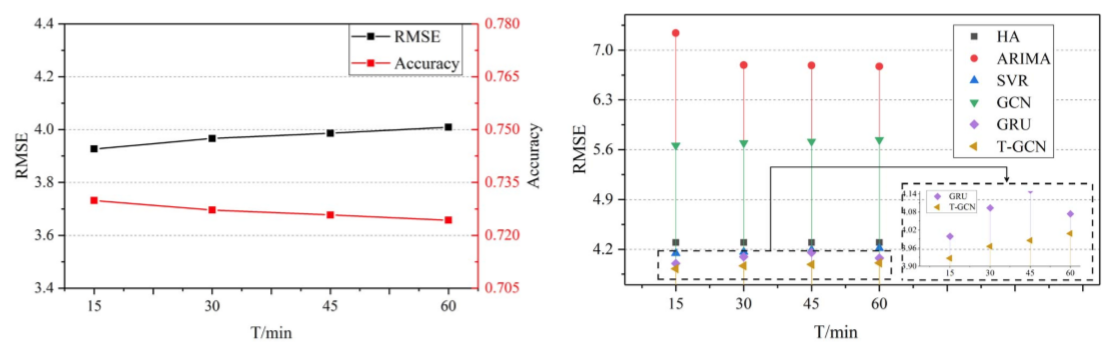
干擾分析與魯棒性：通過向資料中新增兩種不同的噪聲檢驗T-GCN的魯棒性，高斯分佈、泊松分佈的 值作為自變數被改變，分別新增到兩種資料集上，得到結果：

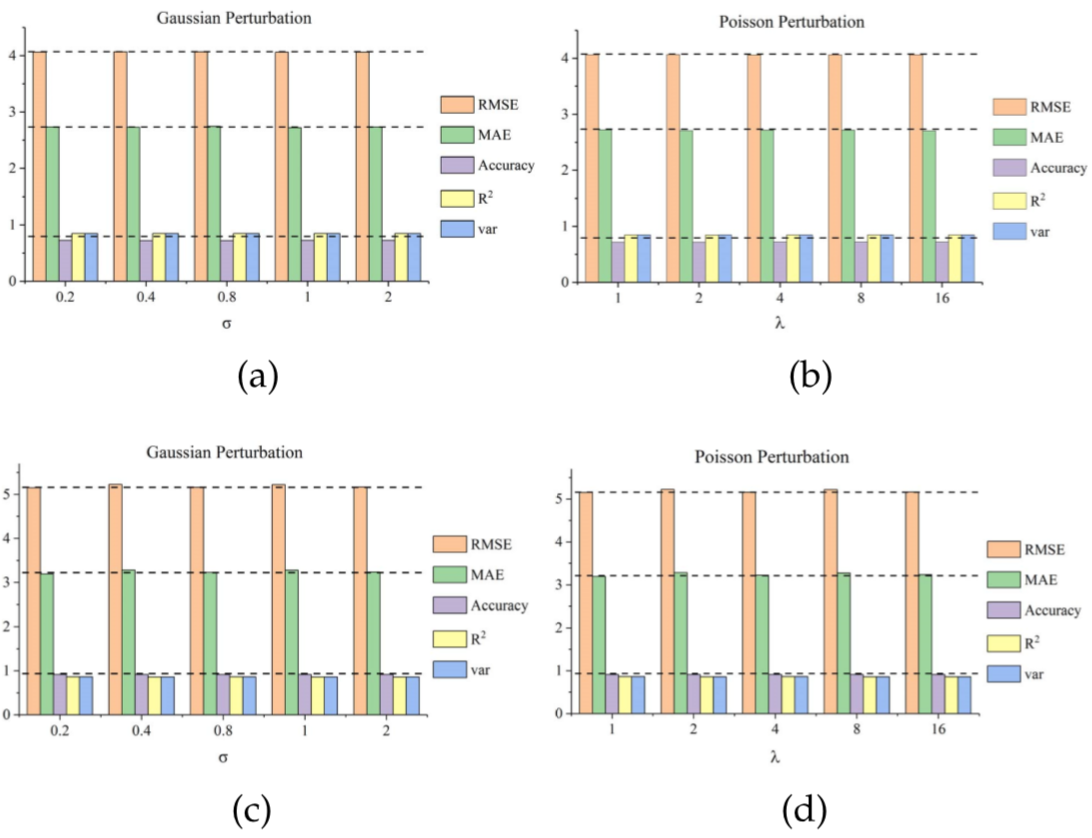
由評估指標的隨噪聲的變化細微可以得出T-GCN具強魯棒性的結論。

模型解釋：

文章將T-GCN所得的預測結果與真實資料視覺化得到結論：

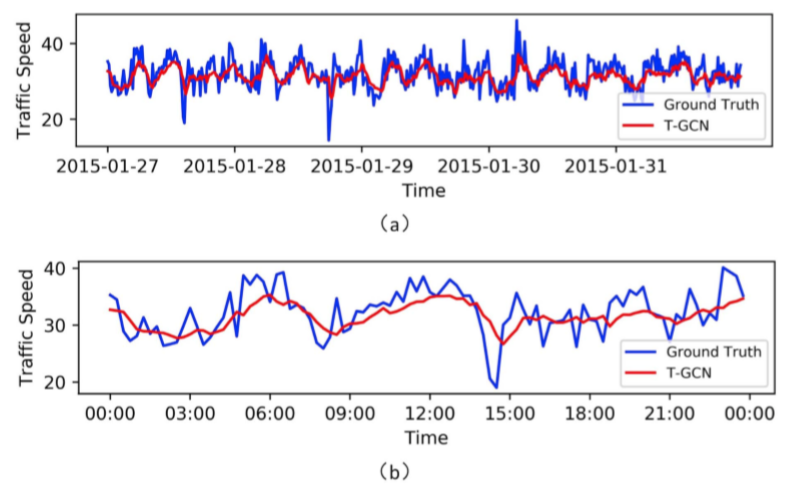
模型對於峰谷值的預測效果不佳，原因在於T-GCN在傅立葉域中定義了平滑過濾器，通過不斷移動過濾器提取空間特徵，造成了全域性預測中的細微變化，使得曲線中的峰變得平滑。

文章還指出預測與實際之間存在固定誤差，由資料集的特殊性造成，即SZ-taxi資料集表示某時刻出租車的數量可能為0，但實際道路上車輛的數量不一定為0；

對這篇論文的解讀就到這裡結束了，Methodology部分使用GCN與GNU的理論，設計了新的計算單元;Experiment部分很讓我受教，對實驗的條件、前提設定的非常詳盡，在介紹資料集與衡量指標後，對選取實驗引數作了嚴格的實驗論證；對實驗結果進行了詳盡的分析，通過與其他幾個模型的預測結果進行對比，從空間、時間、時間跨度預測、精度、魯棒性等角度對模型的優越性進行對比論證，資料的選取與展示都精確地契合了論證的論點；最後關於傅立葉與峰谷偏差的模型解釋很精妙。

關於GNU、LSTM的學習解讀會繼續跟進。同時也會對這篇論文git上的開原始碼進行解讀與實驗復