2. 程式人生 > >機器學習實踐（九）—sklearn之樸素貝葉斯演算法

機器學習實踐（九）—sklearn之樸素貝葉斯演算法

阿新 • • 發佈：2018-11-28

一、樸素貝葉斯演算法

  • 什麼是樸素貝葉斯分類方法

    屬於哪個類別概率大，就判斷屬於哪個類別

  • 概率基礎

    • 概率定義為一件事情發生的可能性
    • P(X) : 取值在[0, 1]
    • 聯合概率、條件概率與相互獨立
      • 聯合概率：包含多個條件，且所有條件同時成立的概率
        • 記作：P(A,B)
      • 條件概率：就是事件A在另外一個事件B已經發生條件下的發生概率
        • 記作：P(A|B)
      • 相互獨立：如果P(A, B) = P(A)P(B)，則稱事件A與事件B相互獨立。

二、樸素貝葉斯公式

P ( C ∣ W ) =

P ( W ∣ C ) P (
C ) P ( W ) P(C|W) = \frac{P(W|C)P(C)}{P(W)}

樸素貝葉斯：特徵之間是相互獨立的。

因此當 W 不存在時，可使用相互獨立將 W 進行拆分

三、簡單案例：

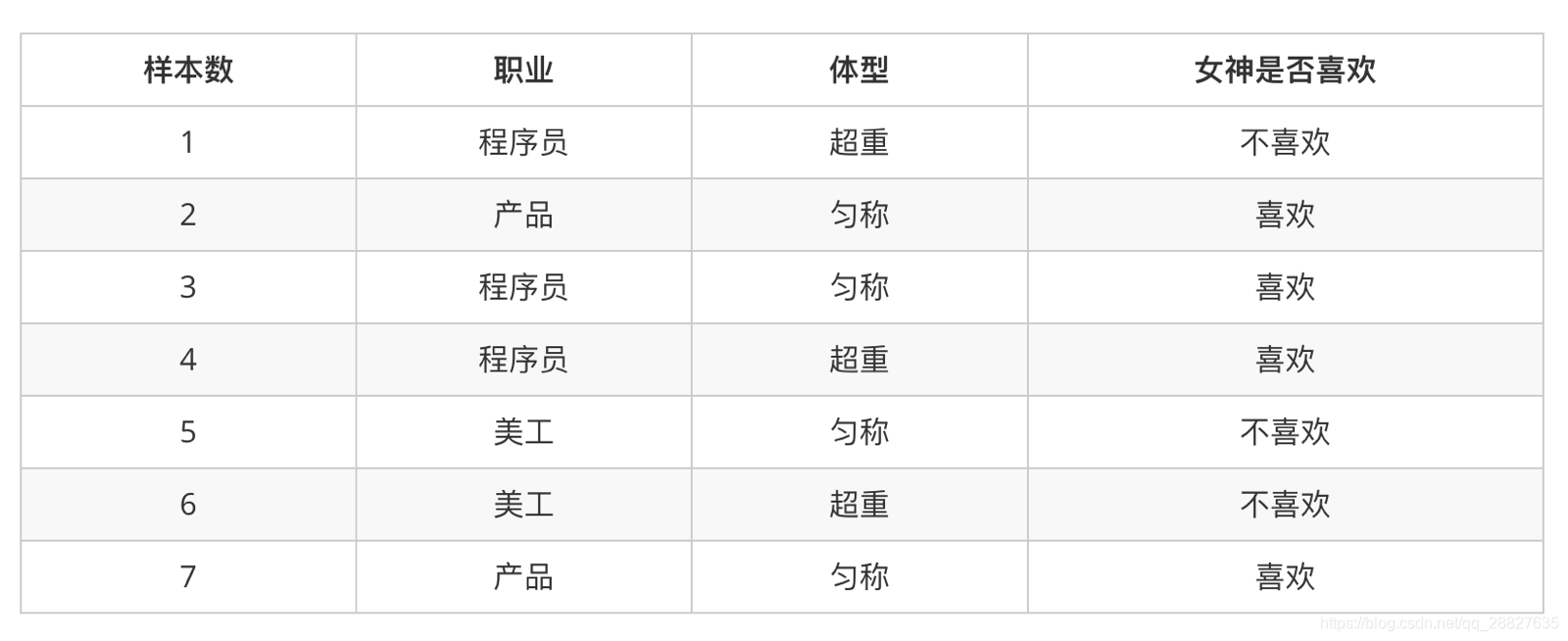
在這裡插入圖片描述

  • 計算下面概率

    • P(喜歡|產品, 超重) = ？

  • 套用公式可得

    P ( 喜 歡 ∣ 產 品 , 超 重 ) = P ( 產 品 , 超 重 ∣ 喜 歡 ) P ( 喜 歡 ) P ( 產 品 , 超 重 ) P(喜歡|產品, 超重) = \frac{P(產品, 超重|喜歡)P(喜歡)}{P(產品, 超重)}

  • 分析

    • 上式中，P(產品, 超重|喜歡) 和 P(產品, 超重) 的結果均為0，導致無法計算結果。
    • 這是因為我們的樣本量太少了，不具有代表性，本來現實生活中，肯定是存在職業是產品經理並且體重超重的人的，P(產品, 超重)不可能為0；而且事件“職業是產品經理”和事件“體重超重”通常被認為是相互獨立的事件，
    • 但是，根據我們有限的7個樣本計算“P(產品, 超重) = P(產品)P(超重)”不成立。
    • 而樸素貝葉斯可以幫助我們解決這個問題。
    • 樸素貝葉斯，簡單理解，就是假定了特徵與特徵之間相互獨立的貝葉斯公式。
    • 也就是說，樸素貝葉斯，之所以樸素，就在於假定了特徵與特徵相互獨立。
    • 所以，如果按照樸素貝葉斯的思路來解決，就可以是：

P ( 產 品 , 超 重 ) = P ( 產 品 ) ∗ P ( 超 重 ) = 2 7 ∗ 3 7 = 6 49 P(產品, 超重) = P(產品) * P(超重) = \frac{2}{7} * \frac{3}{7} = \frac{6}{49}

P ( 產 品 , 超 重 ∣ 喜 歡 ) = P ( 產 品 ∣ 喜 歡 ) ∗ P ( 超 重 ∣ 喜 歡 ) = 1 2 ∗ 1 4 = 1 8 P(產品, 超重|喜歡) = P(產品|喜歡) * P(超重|喜歡) = \frac{1}{2} * \frac{1}{4} = \frac{1}{8}

P ( 喜 歡 ∣ 產 品 , 超 重 ) = P ( 產 品 , 超 重 ∣ 喜 歡 ) P ( 喜 歡 ) P ( 產 品 , 超 重 ) = 1 8 ∗ 4 7 6 49 = 7 12 P(喜歡|產品, 超重) = \frac{P(產品, 超重|喜歡)P(喜歡)}{P(產品, 超重)} = \frac{\frac{1}{8} * \frac{4}{7}}{\frac{6}{49}} = \frac{7}{12}

四、多個特徵的樸素貝葉斯

1. 公式

P ( C ∣ F 1 , F 2 , . . . ) = P ( F 1 , F 2 , . . . ∣ C ) P ( C ) P ( F 1 , F 2 , . . . ) P(C|F_1,F_2,...) = \frac{P(F_1,F_2,...|C)P(C)}{P(F_1,F_2,...)}

C 可以是不同類別

2. 公式分為三個部分：

  • P©：每個文件類別的概率(某文件類別數／總文件數量)
  • P(W│C)：給定類別下特徵（被預測文件中出現的詞）的概率
    • 計算方法：P(F1│C)=Ni/N （訓練文件中去計算）
      • Ni​ 為該F1詞在C類別所有文件中出現的次數
      • N為所屬類別C下的文件所有詞出現的次數和
  • P(F1,F2,…) 預測文件中每個詞的概率

如果計算兩個類別概率比較：

所以我們只要比較前面的大小就可以，得出誰的概率大

四、案例-樸素貝葉斯-文章分類

  • 資料

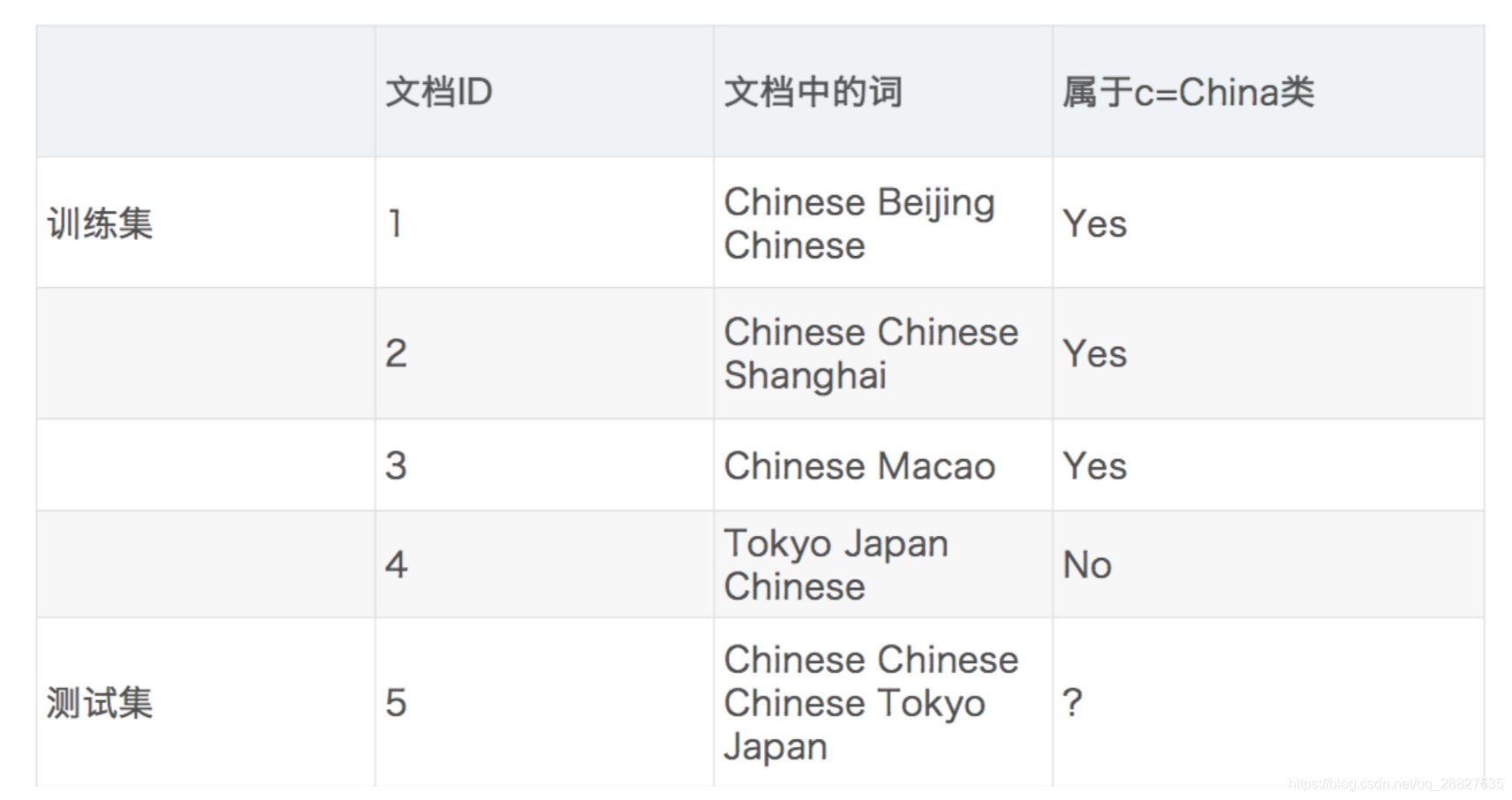
    在這裡插入圖片描述

  • 分別計算屬於兩個類的概率

    • P ( C ∣ C h i n e s e , C h i n e s e , C h i n e s e , T o k y o , J a p a n ) P(C|Chinese, Chinese, Chinese, Tokyo, Japan)
    • P ( n o t C ∣ C h i n e s e , C h i n e s e , C h i n e s e , T o k y o , J a p a n ) P(not C|Chinese, Chinese, Chinese, Tokyo, Japan)

  • 計算過程

    P(C|Chinese, Chinese, Chinese, Tokyo, Japan)
= P(Chinese, Chinese, Chinese, Tokyo, Japan|C) * P(C)
= P(Chinese|C)^3 * P(Tokyo|C) * P(Japan|C) * P(C)
= 5/8 * 0 * 0
P(notC|Chinese, Chinese, Chinese, Tokyo, Japan)
= P(Chinese, Chinese, Chinese, Tokyo, Japan|notC) * P(notC)
= P(Chinese|notC)^3 * P(Tokyo|notC) * P(Japan|notC) * P(notC)
= 1/9 * 1/3 * 1/3

    但是我們發現 P(Tokyo|C) 和 P(Japan|C) 都為 0，這是不合理的，如果詞頻列表裡面有很多出現次數都為 0，很可能計算結果都為 0。

    我們能夠使用拉普拉斯平滑係數解決此問題。

  • 拉普拉斯平滑係數

    P ( F 1 ∣ C ) = N i + α N + α m P(F1|C) = \frac{Ni+\alpha}{N+\alpha m}

    Ni​ 為該F1詞在C類別所有文件中出現的次數。

    N為所屬類別C下的文件所有詞出現的次數和。

    α \alpha 為指定的係數，一般為1。

    m 為訓練集中有多少個特徵詞種類，如在此案例中 m = 6 。

五、sklearn 樸素貝葉斯 API

sklearn.naive_bayes.MultinomialNB(alpha = 1.0)

  • 樸素貝葉斯分類
  • alpha
    • 拉普拉斯平滑係數

六、案例-樸素貝葉斯-20類新聞分類

  • 資料集介紹

在這裡插入圖片描述

  • 步驟分析

    • 進行資料集的分割
    • TFIDF進行的特徵抽取
      • 將文章字串進行單詞抽取
    • 樸素貝葉斯預測

  • 完整程式碼

    • 這裡的轉換器不能對測試集進行 fit 操作，因為 tfidf 轉換器對於不同的文章來說提取的特徵值不同，提取的特徵不同，訓練出的模型就不同

    from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB


# 獲取資料
news = fetch_20newsgroups()

# 劃分資料集
x_train, x_test, y_train, y_test = train_test_split(news.data, news.target
            
      
    
           
    
              
              
    
            
    
            
    相關推薦
    
			   
            
            
            
 

    

    
    
    
    機器學習實踐（九）—sklearn之樸素貝葉斯演算法
    
     
      
 
  
  
 一、樸素貝葉斯演算法 
  
   什麼是樸素貝葉斯分類方法 屬於哪個類別概率大，就判斷屬於哪個類別  
   概率基礎 
    
    概率定義為一件事情發生的可能性 
    P(X) : 取值在[0, 1] 
    
    
    
    聯合概率、條件概率與相互獨立  
    

    
  
 

    

    
    
    
    機器學習實踐（七）—sklearn之K-近鄰演算法
    
     
      
 
  
  
 一、K-近鄰演算法(KNN)原理 
 K Nearest Neighbor演算法又叫KNN演算法，這個演算法是機器學習裡面一個比較經典的演算法， 總體來說KNN演算法是相對比較容易理解的演算法 
  
  
   定義 如果一個樣本在特徵空間中的k個最相似(即特徵空間中最鄰近)的樣本中的 
    

    
  
 

    

    
    
    
    機器學習實踐（六）—sklearn之轉換器和估計器
    
     
      
 
  
  
 一、sklearn轉換器 
  
   想一下之前做的特徵工程的步驟？ 
    
    1 例項化 (例項化的是一個轉換器類(Transformer)) 
    2 呼叫fit_transform(對於文件建立分類詞頻矩陣，不能同時呼叫) 
     
  
  
  
   我們 
    

    
  
 

    

    
    
    
    機器學習實踐（三）—sklearn之特徵工程
    
     
      
 
  
  
 一、特徵工程介紹 
 1. 為什麼需要特徵工程 
 Andrew Ng ： “Coming up with features is difficult, time-consuming, requires expert knowledge. “Applied machine learnin 
    

    
  
 

    

    
    
    
    機器學習實踐（二）—sklearn之資料集
    
     
      
 
  
  
 一、可用資料集 
  
  Kaggle網址：https://www.kaggle.com/datasets 
  UCI資料集網址： http://archive.ics.uci.edu/ml/ 
  scikit-learn網址：http://scikit-learn.org/sta 
    

    
  
 

    

    
    
    
    機器學習實踐（一）—sklearn之概述
    
     
      
 
  
  
 1956年，人工智慧元年。 
 人類能夠創造出人類還未知的東西。 
 這未知的東西人類能夠保證它不誤入歧途嗎。 
  
 一、機器學習和人工智慧，深度學習的關係 
  
   機器學習是人工智慧的一個實現途徑  
   深度學習是機器學習的一個方法發展而來  
  
 二、機器學習，深度 
    

    
  
 

    

    
    
    
    機器學習實踐（五）—sklearn之特徵降維
    
     
      
 
  
  
 一、特徵降維概述 
  
   為什麼要對特徵進行降維處理 
    
    如果特徵本身存在問題或者特徵之間相關性較強，對於演算法學習預測會影響較大 
     
  
  
  
   什麼是降維 
    
    降維是指在某些限定條件下，降低隨機變數(特徵)個數，得到一組“不 
    

    
  
 

    

    
    
    
    機器學習實踐（四）—sklearn之特徵預處理
    
     
      
 
  
  
 一、特徵預處理概述 
  
   什麼是特徵預處理 # scikit-learn的解釋
provides several common utility functions and transformer classes to change raw feature vectors into 
    

    
  
 

    

    
    
    
    機器學習實踐（八）—sklearn之交叉驗證與引數調優
    
     
      
 
  
  
 一、交叉驗證與引數調優 
  
   交叉驗證(cross validation) 
    
    交叉驗證：將拿到的訓練資料，分為訓練集、驗證集和測試集。 
      
      訓練集：訓練集+驗證集 
      測試集：測試集 
       
    
    
    
    

    
  
 

    

    
    
    
    機器學習系列之樸素貝葉斯演算法（監督學習-分類問題）
    
     
     
							
							
							'''
@description ：一級分類：監督學習，二級分類：分類（離散問題），三級分類：貝葉斯演算法
    演算法優點：
        a 樸素貝葉斯模型發源於古典數學理論，有穩定的分類效率
        b 對缺失的資料不太敏感，演算法也比較簡
  
    

    
  
 

    

    
    
    
    資料探勘領域十大經典演算法之—樸素貝葉斯演算法（超詳細附程式碼）
    
     
     
                簡介
NaïveBayes演算法，又叫樸素貝葉斯演算法，樸素：特徵條件獨立；貝葉斯：基於貝葉斯定理。屬於監督學習的生成模型，實現簡單，沒有迭代，並有堅實的數學理論（即貝葉斯定理）作為支撐。在大量樣本下會有較好的表現，不適用於輸入向量的特徵條件有關聯的場景。

基本思想
(1) 
    

    
  
 

    

    
    
    
    機器學習之樸素貝葉斯演算法與程式碼實現
    
     
                                         樸素貝葉斯演算法與程式碼實現

演算法原理
樸素貝葉斯是經典的機器學習演算法之一，也是為數不多的基於概率論的分類演算法。樸素貝葉斯原理簡單，也很容易實現，多用於文字分類，比如垃圾郵件過濾。
該演算法的優點在於簡單易懂、學習效率高、在某些領 
    

    
  
 

    

    
    
    
    【斯坦福---機器學習】複習筆記之樸素貝葉斯演算法
    
     
     
							
							
							本講大綱：

1.樸素貝葉斯（Naive Bayes） 
2.神經網路（Neural Networks） 
3.支援向量機（Support vector machines）



1.樸素貝葉斯

前面講的主要是是二元值的特徵，更一般化的是xi可以取{1，2，3 
    

    
  
 

    

    
    
    
    機器學習實戰中，第四章樸素貝葉斯，過濾垃圾郵件，正則表示式切分郵件內容得出字母的問題解決方法
    
     
     
                原文中的程式碼：listOfTokens = re.split(r'\W*', bigString)



修改為：listOfTokens = re.split(r'\W+', bigString)            
                
         
    

    
  
 

    

    
    
    
    生成學習演算法之樸素貝葉斯演算法
    
     
     
                

2  樸素貝葉斯演算法
在GDA中，特徵向量是連續的實值向量。現在讓我們討論一種不同的學習演算法，在這個演算法中，是離散值。
對於我們的激勵的例子，考慮使用機器學習建立一個電子郵件的垃圾郵件過濾器。這裡，我們希望根據它們是未經請求的商業（垃圾）電子郵件還是非垃圾郵件進行分 
    

    
  
 

    

    
    
    
    【機器學習－西瓜書】七、樸素貝葉斯分類器
    
     
     
							
							
							

推薦閱讀：拉普拉斯修正



7.3樸素貝葉斯分類器

關鍵詞： 樸素貝葉斯；拉普拉斯修正 
上一小節我們知道貝葉斯分類器的分類依據是這公式：P(c∣x)=P(x,c)P(x)=P(c)⋅P(c∣x)P(x) ，對於每個樣本而言，分母P(x)=∑mi=1P( 
    

    
  
 

    

    
    
    
    機器學習基礎——讓你一文學會樸素貝葉斯模型
    
     
     今天這篇文章和大家聊聊樸素貝葉斯模型，這是機器學習領域非常經典的模型之一，而且非常簡單，適合初學者入門。
樸素貝葉斯模型，顧名思義和貝葉斯定理肯定高度相關。之前我們在三扇門遊戲的文章當中介紹過貝葉斯定理，我們先來簡單回顧一下貝葉斯公式：
\[P(A|B)=\frac{P(A)P(B|A)}{P(B)}\]
我 
    

    
  
 

    

    
    
    
    R語言之樸素貝葉斯演算法應用
    
     
     
								
								            
						
                
樸素貝葉斯演算法在R語言中的應用，對應klaR包中的NaiveBayes（）方法。問題描述：主要通過樸素貝葉斯演算法對於測試資料集中的nmkat屬性值進行預測，我們使用的資料是KKNN包中的自帶資料m 
    

    
  
 

    

    
    
    
    機器學習筆記（九）聚類演算法及實踐（K-Means,DBSCAN,DPEAK,Spectral_Clustering）
    
     
     
								
								            
						
                
這一週學校的事情比較多所以拖了幾天，這回我們來講一講聚類演算法哈。
首先，我們知道，主要的機器學習方法分為監督學習和無監督學習。監督學習主要是指我們已經給出了資料和分類，基於這些我們訓練我們的分類器以 
    

    
  
 

    

    
    
    
    非監督學習之k-means聚類演算法——Andrew Ng機器學習筆記（九）
    
     
     
							
							
							寫在前面的話

在聚類問題中，我們給定一個訓練集，演算法根據某種策略將訓練集分成若干類。在監督式學習中，訓練集中每一個數據都有一個標籤，但是在分類問題中沒有，所以類似的我們可以將聚類演算法稱之為非監督式學習演算法。這兩種演算法最大的區別還在於：監督式學習有正確答