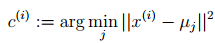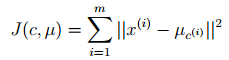寫在前面的話

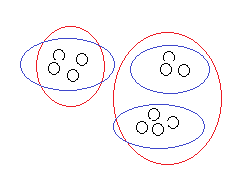
在聚類問題中，我們給定一個訓練集，演算法根據某種策略將訓練集分成若干類。在監督式學習中，訓練集中每一個數據都有一個標籤，但是在分類問題中沒有，所以類似的我們可以將聚類演算法稱之為非監督式學習演算法。這兩種演算法最大的區別還在於：監督式學習有正確答案，而非監督式學習沒有。

比如上面這個訓練集，非監督式學習有可能將它分成兩類也可能是三類，到底哪種分類正確，因情況而定；有時候即便是給定了情況也不見得就能確定。但是監督式學習就完全不一樣。可能隨著學習的深入我們的理解會更加的深刻。

演算法基本內容

演算法的核心目標就是將給定的資料集分成k類，具體做法為：
1、隨機選取k個簇中心（cluster centroids）記為μ

對於每一個類j，重新計算該類的質心

}

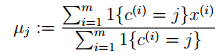
K是我們事先給定的聚類數，c (i)  代表樣本i與k個簇中距離最近的那個簇的下標，c (i)  的值是1到k中的一個。質心μ j  代表我們對屬於同一個類的樣本中心點的猜測。程式就這樣反覆進行直到收斂或者簇中心基本不動。
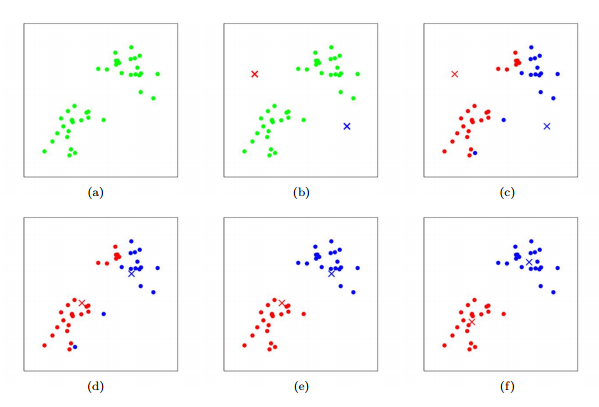
演算法過程可以如下圖示意，其中k取2：

K-means面對的一個重要問題是如何保證收斂，前面的演算法中強調結束條件就是收斂，可以證明的是K-means完全可以保證收斂性。下面我們定性的描述一下收斂性，我們定義畸變函式（distortion function）如下：

J函式表示每個樣本點到其質心的距離平方和。K-means是要將J調整到最小。假設當前J沒有達到最小值，那麼首先可以固定每個簇中心μ j  ，調整每個樣例的所屬的類別c (i)  來讓J函式減少，同樣，固定c (i)  ，調整每個簇中心μ j  也可以使J減小。這兩個過程就是內迴圈中使J單調遞減的過程。當J遞減到最小時，μ 和c 也同時收斂。（在理論上，可以有多組不同的μ 和c 值能夠使得J取得最小值，但這種現象實際上很少見）。其實整體來看，這個演算法就是座標上升演算法（參看《監督學習之再聊支援向量機——Andrew Ng機器學習筆記（六）》的標題4）

如果畸變函式J是非凸函式，意味著我們不能保證取得的最小值是全域性最小值，也就是說k-means對簇中心初始位置的選取比較敏感，但一般情況下k-means達到的區域性最優已經滿足需求。但如果你怕陷入區域性最優，那麼可以選取不同的初始值跑多遍k-means，然後取其中最小的J對應的μ

演算法優點

K-Means聚類演算法的優點主要集中在:
1. 演算法快速、簡單;
2. 對大資料集有較高的效率並且是可伸縮性的;
3. 時間複雜度近於線性，而且適合挖掘大規模資料集。K-Means聚類演算法的時間複雜度是O(nkt) ,其中n代表資料集中物件的數量，t代表著演算法迭代的次數，k代表著簇的數目。

演算法缺點

k-means 演算法缺點
1. 在 K-means 演算法中 K 是事先給定的，這個 K 值的選定是非常難以估計的。很多時候，事先並不知道給定的資料集應該分成多少個類別才最合適。這也是 K-means 演算法的一個不足。有的演算法是通過類的自動合併和分裂，得到較為合理的型別數目 K，例如 ISODATA 演算法。關於 K-means 演算法中聚類數目K 值的確定在文獻中，是根據方差分析理論，應用混合 F統計量來確定最佳分類數，並應用了模糊劃分熵來驗證最佳分類數的正確性。在文獻中，使用了一種結合全協方差矩陣的 RPCL 演算法，並逐步刪除那些只包含少量訓練資料的類。而文獻中使用的是一種稱為次勝者受罰的競爭學習規則，來自動決定類的適當數目。它的思想是：對每個輸入而言，不僅競爭獲勝單元的權值被修正以適應輸入值，而且對次勝單元採用懲罰的方法使之遠離輸入值。
2. 在 K-means 演算法中，首先需要根據初始聚類中心來確定一個初始劃分，然後對初始劃分進行優化。這個初始聚類中心的選擇對聚類結果有較大的影響，一旦初始值選擇的不好，可能無法得到有效的聚類結果，這也成為 K-means演算法的一個主要問題。對於該問題的解決，許多演算法採用遺傳演算法（GA），例如文獻中採用遺傳演算法（GA）進行初始化，以內部聚類準則作為評價指標。
3. 從 K-means 演算法框架可以看出，該演算法需要不斷地進行樣本分類調整，不斷地計算調整後的新的聚類中心，因此當資料量非常大時，演算法的時間開銷是非常大的。所以需要對演算法的時間複雜度進行分析、改進，提高演算法應用範圍。在文獻中從該演算法的時間複雜度進行分析考慮，通過一定的相似性準則來去掉聚類中心的侯選集。而在文獻中，使用的 K-means 演算法是對樣本資料進行聚類，無論是初始點的選擇還是一次迭代完成時對資料的調整，都是建立在隨機選取的樣本資料的基礎之上，這樣可以提高演算法的收斂速度。

參考資料

end