HashMap 詳解五
阿新 • • 發佈:2018-11-28
紅黑樹性質
- 紅黑樹是平衡二叉樹的一種, 但是它的平衡因子是可以大於 1
- 紅黑樹的節點要麼是紅色, 要麼是黑色, 這裡的紅黑色只是用來區分的一種方式, 為了定義規則
- 根節點一定是黑色
- 葉子節點也是黑色, 實際上葉子節點都是由 NULL 組成
- 紅色節點的子節點是黑色
- 根節點到葉子節點的路徑都包含相同數量的黑色節點
紅黑樹與 AVL 樹的區別
紅黑樹線上模擬連結: https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
AVL 樹線上模擬連結: https://www.cs.usfca.edu/~galles/visualization/AVLtree.html
依次插入: 1, 2, 3, 4, 5, 6, 紅黑樹會出現左右子樹高度差大於 1 的情況, AVL 樹就不會, 平衡因子不會超過 1, 最終結果如下:
紅黑樹:
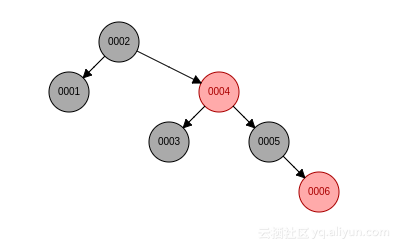
AVL 樹: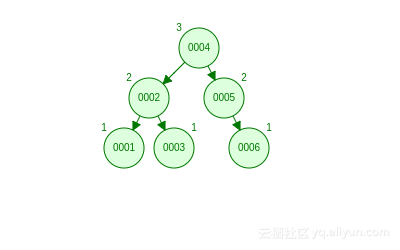
紅黑樹插入
- 節點只有紅黑兩種顏色, 假設插入節點是黑色, 那麼會導致這條路徑的黑色節點比其他路徑要長, 違反性質 6, 所以新節點要為紅色;
- 如果是根節點, 變成黑色, 接下來的操作分兩種情況, 一種是父節點是黑色, 簡稱黑父; 另一種父節點是紅色, 簡稱紅父;
- 黑父, 插入紅節點滿足性質, 什麼都不用做;
-
紅父, 這個情況又要分為兩種情況, 一是紅叔, 一是黑叔;
- 紅叔
將父叔節點變成黑色, 為了不違反性質 6, 祖父節點就變成紅色; 當祖父節點變成紅色, 相當於插入一個新節點到祖父節點的位置, 這時候需要繼續向上迭代, 重新走插入流程. -
黑叔
這個情況就複雜多了, 不僅要改變節點顏色, 還要進行旋轉, 具體可以分為 4 種情況:- 新節點位於祖父節點的左孩子的左子樹, 先右旋, 父節點變成黑色, 祖父節點變成紅色.
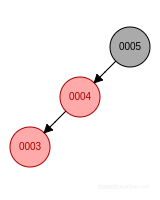
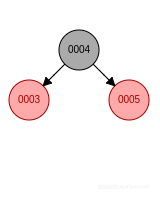
- 新節點位於祖父節點的左孩子的右子樹, 先左旋再右旋, 新節點變成黑色, 祖父節點變成紅色.
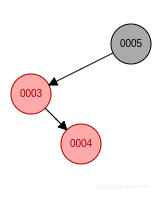
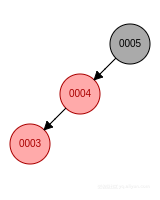
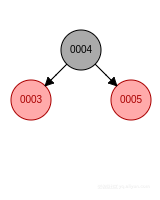
- 新節點位於祖父節點的右孩子的右子樹, 先左旋, 父節點變成黑色, 祖父節點變成紅色.
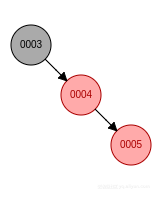
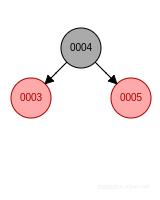
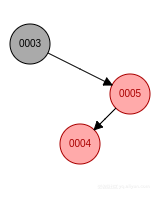
- 新節點位於祖父節點的右孩子的左子樹, 先右旋再左旋, 新節點變成黑色, 祖父節點變成紅色.
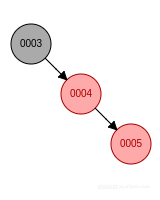

- 新節點位於祖父節點的左孩子的左子樹, 先右旋, 父節點變成黑色, 祖父節點變成紅色.
- 紅叔
putTreeVal()
HashMap 中如果是樹結構, 那麼使用的是紅黑樹結構, 因為查詢的時間複雜度都是 O(logN), 而儲存鍵值對是通過 putTreeVal 方法, 這裡可以看上一 part. 這個方法並不是 HashMap 的方法, 而是 HashMap 的內部類 TreeNode 的方法, 這個內部類用來表示樹節點, 包含幾個屬性: parent, left, right, prev, next, red.
// 返回樹的根節點
final TreeNode<K,V> root() {
for (TreeNode<K,V> r = this, p;;) {
if ((p = r.parent) == null)
return r;
r = p;
}
}
/**
* 如果樹存在相同 key 的節點, 那麼會直接返回這個節點; 如果沒有就插入新節點
* map: 表示 HashMap 本身
* tab: 表示陣列
* h: 表示 key 的雜湊值
* k: 表示 key
* v: 表示 value
*/
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
int h, K k, V v) {
Class<?> kc = null;
boolean searched = false;
// 獲取根節點
TreeNode<K,V> root = (parent != null) ? root() : this;
// 遍歷樹, p 表示當前節點
for (TreeNode<K,V> p = root;;) {
// dir: -1 表示向左遍歷, 1 表示向右遍歷
// ph: 表示當前節點的 key 的雜湊值
// pk: 表示當前節點的 key
int dir, ph; K pk;
// 新節點的雜湊值小於當前節點, 向左遍歷, dir 設定為 -1
if ((ph = p.hash) > h)
dir = -1;
// 新節點的雜湊值大於當前節點, 向右遍歷, dir 設定為 1
else if (ph < h)
dir = 1;
// 新節點的 key 和當前節點相同, 直接返回當前節點
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
// 新節點的雜湊值和當前節點的雜湊值相同, 但是 key 不相同
// comparableClassFor 方法會返回實現 Comparable 介面的型別, 否則返回空
// compareComparables 方法會返回 k 與 pk 比較後的值
// 也就是說這裡是處理當前節點沒有實現 Comparable 介面
// 或者新節點通過 Comparable 介面比較後還是相等的情況
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0) {
// 當前節點的左右子樹可能也相同, 所以向下搜尋符合雜湊值和 key 的節點
if (!searched) {
TreeNode<K,V> q, ch;
searched = true;
if (((ch = p.left) != null &&
(q = ch.find(h, k, kc)) != null) ||
((ch = p.right) != null &&
(q = ch.find(h, k, kc)) != null))
return q;
}
// 比較雜湊值, 小於等於返回 -1, 大於返回 1
dir = tieBreakOrder(k, pk);
}
// 記錄當前節點
TreeNode<K,V> xp = p;
// 根據 dir 判斷左遍歷還是右遍歷, 子節點為空說明來到了葉子節點, 把新節點插入就可以了
if ((p = (dir <= 0) ? p.left : p.right) == null) {
Node<K,V> xpn = xp.next;
// 新節點, next 指向父節點的 next
TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
// 根據 dir 決定是插入到左子樹還是右子樹
if (dir <= 0)
xp.left = x;
else
xp.right = x;
// 這裡設定父子雙向連結串列關係, 把父節點原來的 next 節點的 prev 指向新節點
xp.next = x;
x.parent = x.prev = xp;
if (xpn != null)
((TreeNode<K,V>)xpn).prev = x;
// balanceInsertion() 方法將樹修改成符合紅黑樹性質
// 樹旋轉後可能會根節點轉掉, 那麼陣列索引位置對應節點就不是根節點了
// moveRootToFront() 方法確保索引位置對應根節點
moveRootToFront(tab, balanceInsertion(root, x));
return null;
}
}
}balanceInsertion()
/**
* root: 根節點
* x: 新節點
* 這個方法是把樹改成符合紅黑樹性質的過程, 可以結合上面紅黑樹插入來看
*/
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
TreeNode<K,V> x) {
// 設定新節點為紅色
x.red = true;
// xp: 父節點
// xpp: 祖父節點
// xppl: 祖父節點左孩子
// xppr: 祖父節點右孩子
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
// 父節點為空, 說明這是根節點, 設定成黑色
if ((xp = x.parent) == null) {
x.red = false;
return x;
}
// 黑父, 什麼都不做, 至於還要判斷祖父節點是否為空就不知道為什麼了
else if (!xp.red || (xpp = xp.parent) == null)
return root;
// 紅父, 並且該節點位於祖父節點的左子樹
if (xp == (xppl = xpp.left)) {
// 紅叔, 只要修改顏色即可
// 紅叔變黑叔
// 紅父變黑父
// 祖父節點變紅色
// 新節點指向祖父節點, 繼續向上迭代
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
// 黑叔
else {
// 新節點位於祖父節點的左孩子的右子樹, 需要先左旋, 具體方法看下面
// 左旋完成後當前節點變成父節點, 原來的父節點變成了當前節點, 這是為下面右旋準備
if (x == xp.right) {
root = rotateLeft(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
// 右旋, 具體方法看下面
// 父節點(原來新節點)變黑色, 祖父節點變紅色
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateRight(root, xpp);
}
}
}
}
// 紅父, 並且該節點是祖父節點的右子樹
else {
// 紅叔, 只要修改顏色即可, 參考上面
if (xppl != null && xppl.red) {
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
// 黑叔
else {
// 新節點位於祖父節點右孩子的左子樹, 需要先右旋
if (x == xp.left) {
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
// 然後統一左旋, 處理跟上面一樣
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
}
}
}
}
/**
* 左旋, 實際是通過修改節點的父與子指標來實現
* root: 根節點
* p: 新節點的父節點
*/
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
TreeNode<K,V> p) {
// r: p 的右孩子
// pp: p 的父節點
// rl: p 的右孩子的左孩子
TreeNode<K,V> r, pp, rl;
// 過濾引數錯誤的情況, 判斷是否能夠進行左旋
if (p != null && (r = p.right) != null) {
if ((rl = p.right = r.left) != null)
rl.parent = p;
if ((pp = r.parent = p.parent) == null)
(root = r).red = false;
else if (pp.left == p)
pp.left = r;
else
pp.right = r;
r.left = p;
p.parent = r;
}
return root;
}
/**
* 右旋, 實際是通過修改節點的父與子指標來實現
*/
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
TreeNode<K,V> p) {
// l: p 的左孩子
// pp: p 的父節點
// lr: p 的左孩子的右孩子
TreeNode<K,V> l, pp, lr;
if (p != null && (l = p.left) != null) {
if ((lr = p.left = l.right) != null)
lr.parent = p;
if ((pp = l.parent = p.parent) == null)
(root = l).red = false;
else if (pp.right == p)
pp.right = l;
else
pp.left = l;
l.right = p;
p.parent = l;
}
return root;
}moveRootToFront
/**
* 紅黑樹經過旋轉後有可能修改根節點, 該方法把陣列索引位置指向新根節點, 並修改對應的前後節點
* tab: 儲存陣列
* root: 根節點
*/
static <K,V> void moveRootToFront(Node<K,V>[] tab, TreeNode<K,V> root) {
int n;
if (root != null && tab != null && (n = tab.length) > 0) {
int index = (n - 1) & root.hash;
TreeNode<K,V> first = (TreeNode<K,V>)tab[index];
// 索引位置不是根節點
if (root != first) {
Node<K,V> rn;
tab[index] = root;
TreeNode<K,V> rp = root.prev;
// 既然重置了根節點, 那麼雙向連結串列的頭結點就只能是新根節點
// 所以需要對樹的雙向連結串列進行重置了
// 把根節點前後節點進行連線, 同時根節點 next 指向原來頭節點
// 假設原來的雙向連結串列結構是: A<=>B<=>C<=>D, 其中 C 為新根節點
// 那麼先將 C 前後節點 B D 連線: C, A<=>B<=>D
// 然後 C 和原來頭結點 A 連線: C<=>A<=>B<=>D
if ((rn = root.next) != null)
((TreeNode<K,V>)rn).prev = rp;
if (rp != null)
rp.next = rn;
if (first != null)
first.prev = root;
root.next = first;
root.prev = null;
}
assert checkInvariants(root);
}
}經過上面的分析我們就可以得出 HashMap 對於樹節點插入的大概過程了.
- 從根節點開始遍歷, 比較雜湊值, 小於就向左遍歷, 大於就向右遍歷, 等於就返回節點;
- 遍歷到最後把新節點插入, 這時候要看新節點是位於祖父節點的左子樹還是右子樹, 還要看父叔節點顏色;
- 新節點是祖父左子樹, 並且紅父紅叔, 那麼只要修改顏色即可;
- 新節點是祖父左子樹, 並且紅父黑叔, 這時如果是位於父節點的右子樹, 需要先左旋, 然後統一右旋和修改顏色;
- 新節點是祖父右子樹, 並且紅父紅叔, 那麼同樣只修改顏色即可;
- 新節點是祖父右子樹, 並且紅父黑叔, 這時如果是位於父節點的左子樹, 需要先右旋, 然後統一左旋和修改顏色.
篇幅原因, 關於樹的另一個方法 treeifyBin() 就留到下一 part 再來講.
