原文連結：https://blog.safe.com/2018/07/fme-and-convolution-evangelist176/

卷積理論

FME 2018.1增加了卷積的能力。

卷積是對兩個物件進行數學運算，以便建立第三個物件。在FME術語中，第一個物件是柵格要素，第二個物件是類似柵格的數字矩陣。該操作可以是許多常見的數學運算之一。

使用指定的運算子，利用矩陣處理柵格，返回具有新質量的柵格要素。

理解了？OK，這是一個用於輕微模糊影像的矩陣：

例如. 柵格#1（上圖左） 加上矩陣，返回略微模糊的柵格#2（上圖右）。

如果它有幫助，矩陣和操作的組合被稱作“濾波”。所以你選擇一個柵格檔案，並對其應用濾波。一些人們還稱之為“透鏡”和“透鏡處理”。

它實際做了什麼？

如果你跟我一樣，你會想知道到底發生了什麼，因此我將深入瞭解一些細節。如果這不適合你，請跳到“FME中的卷積”部分。

還停留在這裡？OK，所以發生的事情是濾波器遍歷柵格中的每個單元，利用周圍的值和矩陣的值，重新計算單元的新值。

舉個例子，我們使用這個小方塊的柵格資料，中心單元的紅色波段值為218，使用模糊濾波：

通過數字濾波器將值218轉換為200。為什麼？好吧，如果我的數學正確，等式為：

例：在3×3中的每個單元乘以其對應的核並求和。然後除以核的總和16，得到中心單元的新值200。

基本上它是周圍值的平均值，每個值通過核進行加權。因此，上述核給予中心單元最高權重（4），鄰近單元中等權重（2），對角相鄰單元給予低權重（1）。

對應用的柵格要素的每個波段、每個單元重複這個過程，產生期望的輸出。計算只對原始值進行操作。當演算法處理下一個單元（如上）時，它的鄰近值為218，而不是200.

我相信“對應”的矩陣值是相反的（所以對於133*1，這裡的“1”是矩陣右下角的值），但是這裡的核矩陣是對稱的，所以沒有區別。

濾波型別

不同的濾波有不同的核以及不同的操作型別（一些為增加，一些為求平均值），所以會產生明顯不同的效果。

我不知道為什麼上述的過程產生模糊，但即使知道它通常如何工作也很重要。例如，它說明了模糊演算法不是簡單的降低解析度（其他方法有可能是這樣），而是通過操縱單元格顏色來建立模糊。

我注意到像上面的核，是一組正數，除數為這些值的總和。它們往往是模糊（平滑）濾波。但我也注意到具有負值的核：

這些核值加起來得到一個除數。它們通常用於銳化影象或檢測影象邊緣。我相信（我不是專家）如果數字大於或小於0，當FME使用該濾波時，影象變暗或明亮。

無論如何，我認為這是我關於濾波和核值理論的知識極限。 讓我們來看看它是如何在FME中實現的......

FME中的卷積

FME中執行卷積的轉換器是RasterConvolver。它的別名是RasterLensProcessor，對於快速新增，“nvo” 或 “rlp”是用於找到它的唯一程式碼。

RasterConvolver的引數對話方塊如下所示：

頂部下拉選項顯示了一組不同的預置濾波器：

所以你可以使用它們中的任意一個對你的柵格資料進行處理，併產生一定的效果。例如，這有一個用於高程模型的線檢測核。

選擇一個固定濾波器會自動設定核、除數和操作欄位。你只需要更改它們就可以建立自定義濾波器。說到哪…

自定義濾波器

我想建立一個自定義濾波器，例如模糊效果還不夠，我希望一個更大的模糊。這很簡單，我只需要編輯對話方塊中的值：

這裡我只更改了權重，並設定匹配的除數，雖然我可以設定一個不同的核大小或操作。順便說一下，我們允許的核大小通常為3×3, 5×5, 7×7, 9×9, 和11×11。不允許非正方形核。

這些變化導致的結果（從左到右）原始—高斯濾波—使用者自定義濾波：

注意濾波使得底部文字逐漸不便閱讀。放大後差異更明顯：

但是矩陣中的數字意味著什麼。我所做的就是通過減少中心權重和增加周圍的權重，將權重從中心轉移到周圍的單元上。除數現在為21，因為權重增加到21。為了儲存這些數字，我還可以設定Divisor（除數）為特定設定“Sum of Kernel Weights”:

我花了一些時間來研究和理解這個概念，我並不會覺得卷積就是這麼簡單。但是，很容易通過設定來進行試驗，檢視發生的情況，包括一些高階選項。

高階選項

RasterConvolver有一些高階控制選項。它們的影響不大，但是可能很重要，這是我在這裡提到它們的原因。

動態核函式

我把它們稱為動態核函式，因為我想不出來其他的稱呼了。實際上就是你可以通過屬性、使用者引數或條件值來設定核權重。通過把kernel size設定為“Derived from Weights”實現：

現在我有一個文字欄位而非網格來定義核值，可以有多種方法。這個引數接受空格分割的浮點數列表。只接受矩形核函式，但是你可以設定權重為0以避免使用某些單元格，並建立自定義形狀。

邊緣處理

關鍵的考慮是在影象邊緣發生什麼。如果每個新的單元格都使用它的鄰近值進行計算，對於一側沒有鄰近值的邊緣單元格來說會發生什麼？FME對此有相應的設定：

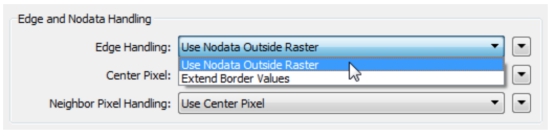
當單元格缺失時，FME給你選項：使用Nodata值或將邊界值擴充套件到空的區域。結果的差異（對於一個5×5的高斯濾波）如下：

這是西南角，所以檢視左邊和底部邊緣。使用Nodata（左邊的影象）似乎給出了更生硬的邊界，邊界線更清晰。擴充套件邊界值給出了更柔和的邊界。如果我想要進行邊緣檢測，我想我會首先嚐試設定擴充套件值，否則柵格邊框可能會被誤解為邊緣（我很可能是錯的）。

Nodata 處理

說到Nodata，柵格中的Nodata值會發生什麼取決於一組引數：Center Pixel和Neighbor Pixel：

Center Pixel處理的場景為：待處理的畫素值為Nodata。它可以輸出為Nodata或忽略Nodata。相似的鄰近畫素如果為Nodata，可以被忽略，或使用中心畫素值替換。如果你知道有Nodata值，我懷疑你只會忽略Nodata，大概這就是它是預設設定值的原因。

最後，一個不受引數控制的高階選項是對柵格特定波段進行卷積的能力；例如我想對RGB影象中的紅、綠波段進行卷積，而不對藍波段進行操作。為了做到這個，我只需要在RasterConvolver前新增一個RasterSelector，以便定義待處理的波段。

為什麼要卷積?

瞭解了這些，這個轉換器的實際應用是什麼？

首先它用於影象處理，例如模糊和銳化影象。你可能不覺得很有用，但是模糊（平滑）影象有助於隱藏噪聲、產生細節。我們來看這個示例，我們希望定位海洋中船的位置，使用簡單的高斯濾波：

雖然我們要找的船更加模糊，但是卷積去除了水面上的極端反射。當我搜索在整個影象搜尋亮點來找船時（使用RasterExpressionEvaluator），區別在於：

沒有卷積的影象具有上千個可能是船的亮點。卷積後的影象具有三個明顯點。即使是船的尾跡也被清理乾淨了。

所以這樣的核函式對於影象分類是有用的。除了在海上定位船舶外，它們還可以幫助你提取建築區域，評估農業清單或模擬洪水影響。此外，一系列柵格影象可以顯示隨著時間的推移，船舶所在的位置，有助於追蹤特定船舶的位置或它來自何處。甚至可以進行車輛監測和追蹤！

從柵格影象中提取向量幾何影象是另外常見的需求。第一步通常是邊緣檢測，卷積對此也有用。RasterConvolver轉換器又很多不同的邊緣檢測核。

我無法建立一個我非常滿意的空間示例，但我確實發現它們也可以從先前的平滑例子中受益。該影象是各種非空間邊緣檢測的示例。

另外，如圖所示，RasterConvolver不侷限於影象。它也可以處理柵格DEM。例如，我找到一個生成坡度的核。我用它對我的資料進行處理，得到與RasterSlopeCalculator轉換器（Percent Rise模式）相同的結果。為了清晰可見，轉到Int8，它看起來如下所示：

好吧，我說“完全”。它在Data Inspector中看起來完全一樣，但是數字略有不同。我認為這兩個結果只是在不同的尺度上。我將使用RasterSlopeCalculator作為最終的答案，因為它告訴我數字的含義（坡度百分比），而我不確定卷積的數字是否真正代表什麼。但是，它顯示了在DEM資料集上使用RasterConvolver你可以做的事情。

順便說一下，我的工作空間是這樣的：

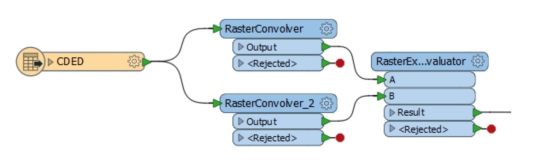
為什麼有兩個卷積？嗯，坡度/線檢測在不同方向應用時會產生不同的結果。所以我用平行工作流將它應用到水平和豎直兩個方向，然後使用RasterExpressionEvaluator將資料重新組合在一起以將其合併：

我發現這個表示式比我最開始使用的對兩個柵格取平均值更好。你可以在我們的knowledgebase找到例子。

總結

Merriam-Webster告訴我，卷積來自同一個拉丁詞（volvere，意為“滾動”）“convoluted”（意思是複雜的）。我相信這點！這個主題有點複雜和令人費勁！ 但是，FME可以輕鬆選擇預定義的卷積濾波器並嘗試自定義濾波器。

我對於FME處理資料的速度印象很深。它只用了22秒對40個柵格瓦片（每個大小為1600 x 1000畫素，具有3個波段）進行讀取、卷積和寫出。

我已經把我的兩個示例放到我們的knowledgebase（邊緣檢測和坡度計算）並將很快放上第三個示例，你可能想進一步探索。總的來說有很多使用者對這個轉換器有需求，所以它應該會很流行。趕快下載FME2018.1並試試使用它。

同時我也注意到FME新的2018.1版本還介紹了RasterStatisticsCalculator 轉換器，用於計算每個柵格波段或調色盤的最小、最大、平均值等。我相信你會發現這個轉換器同樣非常有用。