必須知道的八大種排序演算法【java實現】
阿新 • • 發佈:2018-11-29
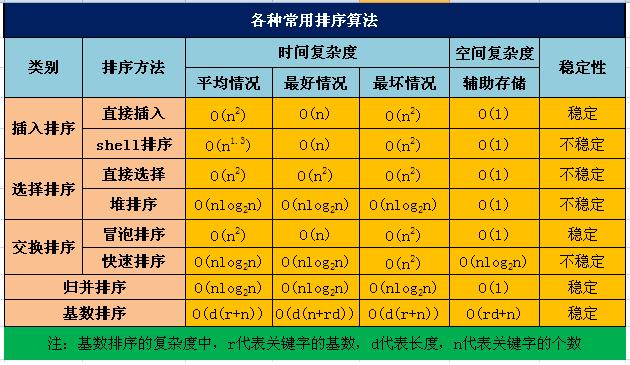
各種演算法的時間複雜度:
package com.lianxi; import java.util.Arrays; public class Sort { /** * 八種排序演算法 */ public static void main(String[] args) { int[] numbers = {11,2,3,1,454,66,34,123,67,99}; System.out.println("氣泡排序:"+Arrays.toString(bubbleSort(numbers))); System.out.println("選擇排序:"+Arrays.toString(selectSort(numbers))); System.out.println("插入排序:"+Arrays.toString(insertSort(numbers))); System.out.println("希爾排序:"+Arrays.toString(shellSort(numbers))); System.out.println("快速排序:"+Arrays.toString(quick(numbers))); System.out.println("歸併排序:"+Arrays.toString(guiBinSort(numbers,0,numbers.length-1))); } /** * 氣泡排序 * 比較相鄰的元素。如果第一個比第二個大,就交換他們兩個。 * 對每一對相鄰元素作同樣的工作,從開始第一對到結尾的最後一對。在這一點,最後的元素應該會是最大的數。 * 針對所有的元素重複以上的步驟,除了最後一個。 * 持續每次對越來越少的元素重複上面的步驟,直到沒有任何一對數字需要比較。 * @param numbers 需要排序的整型陣列 */ public static int[] bubbleSort(int[] numbers) { int temp = 0; int size = numbers.length; for(int i = 0 ; i < size-1; i ++) { for(int j = 0 ;j < size-1-i ; j++) { if(numbers[j] > numbers[j+1]) //交換兩數位置 { temp = numbers[j]; numbers[j] = numbers[j+1]; numbers[j+1] = temp; } } } return numbers; } /** * 選擇排序演算法 * 在未排序序列中找到最小元素,存放到排序序列的起始位置 * 再從剩餘未排序元素中繼續尋找最小元素,然後放到排序序列末尾。 * 以此類推,直到所有元素均排序完畢。 * @param numbers */ public static int[] selectSort(int[] numbers) { int size = numbers.length; // 陣列長度 int temp = 0 ; // 中間變數 for(int i = 0 ; i < size ; i++) { int k = i; // 待確定的位置 //選擇出應該在第i個位置的數 for(int j = size -1 ; j > i ; j--) { if(numbers[j] < numbers[k]) { k = j; } } // 交換兩個數 temp = numbers[i]; numbers[i] = numbers[k]; numbers[k] = temp; } return numbers; } /** * 插入排序 * * 從第一個元素開始,該元素可以認為已經被排序 * 取出下一個元素,在已經排序的元素序列中從後向前掃描 * 如果該元素(已排序)大於新元素,將該元素移到下一位置 * 重複步驟3,直到找到已排序的元素小於或者等於新元素的位置 * 將新元素插入到該位置中 * 重複步驟2 * @param numbers 待排序陣列 */ public static int[] insertSort(int[] numbers) { int size = numbers.length; int temp = 0 ; int j = 0; for(int i = 0 ; i < size ; i++) { temp = numbers[i]; //假如temp比前面的值小,則將前面的值後移 for(j = i ; j > 0 && temp < numbers[j-1] ; j --) { numbers[j] = numbers[j-1]; } numbers[j] = temp; } return numbers; } /**希爾排序的原理:根據需求,如果你想要結果從大到小排列,它會首先將陣列進行分組,然後將較大值移到前面,較小值 * 移到後面,最後將整個陣列進行插入排序,這樣比起一開始就用插入排序減少了資料交換和移動的次數,可以說希爾排序是加強 * 版的插入排序 * 拿陣列5, 2, 8, 9, 1, 3,4來說,陣列長度為7,當increment為3時,陣列分為兩個序列 * 5,2,8和9,1,3,4,第一次排序,9和5比較,1和2比較,3和8比較,4和比其下標值小increment的陣列值相比較 * 此例子是按照從大到小排列,所以大的會排在前面,第一次排序後陣列為9, 2, 8, 5, 1, 3,4 * 第一次後increment的值變為3/2=1,此時對陣列進行插入排序, *實現陣列從大到小排 */ public static int[] shellSort(int[] data) { int j = 0; int temp = 0; //每次將步長縮短為原來的一半 for (int increment = data.length / 2; increment > 0; increment /= 2) { for (int i = increment; i < data.length; i++) { temp = data[i]; for (j = i; j >= increment; j -= increment) { if(temp < data[j - increment])//如想從小到大排只需修改這裡 { data[j] = data[j - increment]; } else { break; } } data[j] = temp; } } return data; } /** * 查找出中軸(預設是最低位low)的在numbers陣列排序後所在位置 * @param numbers 帶查詢陣列 * @param low 開始位置 * @param high 結束位置 * @return 中軸所在位置 */ public static int getMiddle(int[] numbers, int low,int high) { int temp = numbers[low]; // 陣列的第一個作為中軸 while(low < high) { while(low < high && numbers[high] > temp) { high--; } numbers[low] = numbers[high];// 比中軸小的記錄移到低端 while(low < high && numbers[low] < temp) { low++; } numbers[high] = numbers[low] ; // 比中軸大的記錄移到高階 } numbers[low] = temp ; // 中軸記錄到尾 return low ; // 返回中軸的位置 } /** * @param numbers 帶排序陣列 * @param low 開始位置 * @param high 結束位置 */ public static void quickSort(int[] numbers,int low,int high) { if(low < high) { int middle = getMiddle(numbers,low,high); //將numbers陣列進行一分為二 quickSort(numbers, low, middle-1); //對低欄位表進行遞迴排序 quickSort(numbers, middle+1, high); //對高欄位表進行遞迴排序 } } /** * 快速排序 * @param numbers 帶排序陣列 */ public static int[] quick(int[] numbers) { if(numbers.length > 0) //檢視陣列是否為空 { quickSort(numbers, 0, numbers.length-1); } return numbers; } /** * 歸併排序 * 簡介:將兩個(或兩個以上)有序表合併成一個新的有序表 即把待排序序列分為若干個子序列,每個子序列是有序的。然後再把有序子序列合併為整體有序序列 * 時間複雜度為O(nlogn) * 穩定排序方式 * @param nums 待排序陣列 * @return 輸出有序陣列 */ public static int[] guiBinSort(int[] nums, int low, int high) { int mid = (low + high) / 2; if (low < high) { // 左邊 guiBinSort(nums, low, mid); // 右邊 guiBinSort(nums, mid + 1, high); // 左右歸併 merge(nums, low, mid, high); } return nums; } /** * 將陣列中low到high位置的數進行排序 * @param nums 待排序陣列 * @param low 待排的開始位置 * @param mid 待排中間位置 * @param high 待排結束位置 */ public static void merge(int[] nums, int low, int mid, int high) { int[] temp = new int[high - low + 1]; int i = low;// 左指標 int j = mid + 1;// 右指標 int k = 0; // 把較小的數先移到新陣列中 while (i <= mid && j <= high) { if (nums[i] < nums[j]) { temp[k++] = nums[i++]; } else { temp[k++] = nums[j++]; } } // 把左邊剩餘的數移入陣列 while (i <= mid) { temp[k++] = nums[i++]; } // 把右邊邊剩餘的數移入陣列 while (j <= high) { temp[k++] = nums[j++]; } // 把新陣列中的數覆蓋nums陣列 for (int k2 = 0; k2 < temp.length; k2++) { nums[k2 + low] = temp[k2]; } } }
輸出:
氣泡排序:[1, 2, 3, 11, 34, 66, 67, 99, 123, 454]
選擇排序:[1, 2, 3, 11, 34, 66, 67, 99, 123, 454]
插入排序:[1, 2, 3, 11, 34, 66, 67, 99, 123, 454]
希爾排序:[1, 2, 3, 11, 34, 66, 67, 99, 123, 454]
快速排序:[1, 2, 3, 11, 34, 66, 67, 99, 123, 454]
歸併排序:[1, 2, 3, 11, 34, 66, 67, 99, 123, 454]
堆排序演算法
1、基本思想:
堆排序是一種樹形選擇排序,是對直接選擇排序的有效改進。
堆的定義下:具有n個元素的序列 (h1,h2,...,hn),當且僅當滿足(hi>=h2i,hi>=2i+1)或(hi<=h2i,hi<=2i+1) (i=1,2,...,n/2)時稱之為堆。在這裡只討論滿足前者條件的堆。由堆的定義可以看出,堆頂元素(即第一個元素)必為最大項(大頂堆)。完全二 叉樹可以很直觀地表示堆的結構。堆頂為根,其它為左子樹、右子樹。
思想:初始時把要排序的數的序列看作是一棵順序儲存的二叉樹,調整它們的儲存序,使之成為一個 堆,這時堆的根節點的數最大。然後將根節點與堆的最後一個節點交換。然後對前面(n-1)個數重新調整使之成為堆。依此類推,直到只有兩個節點的堆,並對 它們作交換,最後得到有n個節點的有序序列。從演算法描述來看,堆排序需要兩個過程,一是建立堆,二是堆頂與堆的最後一個元素交換位置。所以堆排序有兩個函式組成。一是建堆的滲透函式,二是反覆呼叫滲透函式實現排序的函式。
package com.lianxi;
import java.util.Arrays;
public class HeapSort {
public static void main(String[] args) {
int[] a={49,38,65,97,76,13,27,49,78,34,12,64};
int arrayLength=a.length;
// 迴圈建堆
for(int i=0;i<arrayLength-1;i++){
// 建堆
buildMaxHeap(a,arrayLength-1-i);
// 交換堆頂和最後一個元素
swap(a,0,arrayLength-1-i);
System.out.println(Arrays.toString(a));
}
}
// 對data陣列從0到lastIndex建大頂堆
public static void buildMaxHeap(int[] data, int lastIndex){
// 從lastIndex處節點(最後一個節點)的父節點開始
for(int i=(lastIndex-1)/2;i>=0;i--){
// k儲存正在判斷的節點
int k=i;
// 如果當前k節點的子節點存在
while(k*2+1<=lastIndex){
// k節點的左子節點的索引
int biggerIndex=2*k+1;
// 如果biggerIndex小於lastIndex,即biggerIndex+1代表的k節點的右子節點存在
if(biggerIndex<lastIndex){
// 若果右子節點的值較大
if(data[biggerIndex]<data[biggerIndex+1]){
// biggerIndex總是記錄較大子節點的索引
biggerIndex++;
}
}
// 如果k節點的值小於其較大的子節點的值
if(data[k]<data[biggerIndex]){
// 交換他們
swap(data,k,biggerIndex);
// 將biggerIndex賦予k,開始while迴圈的下一次迴圈,重新保證k節點的值大於其左右子節點的值
k=biggerIndex;
}else{
break;
}
}
}
}
// 交換
private static void swap(int[] data, int i, int j) {
int tmp=data[i];
data[i]=data[j];
data[j]=tmp;
}
}
輸出:
[12, 76, 65, 49, 34, 64, 27, 49, 38, 13, 78, 97]
[13, 49, 65, 49, 34, 64, 27, 12, 38, 76, 78, 97]
[38, 49, 64, 49, 34, 13, 27, 12, 65, 76, 78, 97]
[12, 49, 38, 49, 34, 13, 27, 64, 65, 76, 78, 97]
[27, 49, 38, 12, 34, 13, 49, 64, 65, 76, 78, 97]
[13, 34, 38, 12, 27, 49, 49, 64, 65, 76, 78, 97]
[27, 34, 13, 12, 38, 49, 49, 64, 65, 76, 78, 97]
[12, 27, 13, 34, 38, 49, 49, 64, 65, 76, 78, 97]
[13, 12, 27, 34, 38, 49, 49, 64, 65, 76, 78, 97]
[12, 13, 27, 34, 38, 49, 49, 64, 65, 76, 78, 97]