圖的儲存及基本操作
5.3 圖的儲存及基本操作★3◎2
相對於其他的線性資料結構,圖的儲存要複雜很多,因為頂點數相同的圖,其邊(或弧)的數量相差很大。比如一個有n個頂點e條邊的圖,若是以頂點為結點來儲存,由於各個頂點的度數不一致,無法指定結點的指標域中需要的指標數。雖然可以定義結點的指標域存在n-1個指標,但這樣儲存過於複雜,儲存密度過小;若以邊為結點來儲存,又不便於頂點遍歷。所以一般情況下,圖需要同時儲存頂點和邊的資訊。
1.鄰接矩陣法
鄰接矩陣法又稱陣列表示法,是儲存圖的最簡單方法,它的基本思想是用一個n×n的鄰接矩陣表示圖中的邊或弧的資訊,用一個n維向量來儲存n個頂點的資訊,其中針對“圖”和“網”, 鄰接矩陣有不同的解釋。
(1)圖的鄰接矩陣
設G
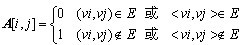
即如果頂點vi和vj之間存在一條邊或弧,定義A[i,j]為1,否則定義為0。
比如圖5-1(a)中的有向圖和圖5-1(b)中的無向圖的鄰接矩陣分別如圖5-2中矩陣A1和矩陣A2所示。

無向圖的鄰接矩陣是一個對稱矩陣。
圖的鄰接矩陣可以很方便地應用於以下兩個方面:
① 判斷任意兩個頂點之間是否有邊相連線。
當A[i,j]取值為1時,頂點Vi和頂點Vj存在邊或弧直接連線。
當A[i,j]取值為0時,頂點Vi和頂點Vj不存在邊或弧直接連線。
② 獲取頂點的度、入度或出度
在無向圖的鄰接矩陣中,第i行或第i列上的所有非0元素的個數就是頂點Vi的度。比如圖5-2(b)中:
TD(V1)=3;TD(V2)=2;TD(V3)=1;TD(V4)=2。
在有向圖的鄰接矩陣中,第i行上的所有非0元素的個數就是頂點Vi的出度,第i列上的所有非0元素的個數就是頂點Vi的入度,兩者之和就是頂點Vi的度。比如圖5-2(a)中:
OD(V1)=3;ID(V1)=1;TD(V1)=4;
OD(V2)=1;ID(V2)=1;TD(V2)=2;
OD(V3)=0;ID(V3)=1;TD(V3)=1;
OD(V4)=1;ID(V4)=2;TD(V4)=3;
(2)網的鄰接矩陣
網與圖的區別是網的每條路徑之間都帶有權值,因此網的鄰接矩陣當中必須能夠儲存此權值,定義網的鄰接矩陣如下:
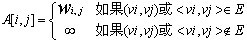
其中:① 邊(vi,vj)或弧<vi,vj>上的權值;② ∞表示無窮大,在計算機中常常用一個大於所有邊的權值的數來代替。
即如果頂點vi和vj之間存在一條邊或弧,定義A[i,j]此邊或弧的權值,否則定義為無窮大。
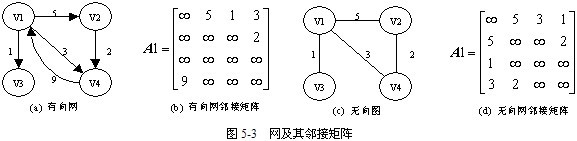
例如圖5-3中(a)和(c)分別為有向網和無向網,(b)和(d)分別是其對應的鄰接矩陣。
(3)鄰接矩陣的儲存結構表示
如下定義了一個鄰接矩陣描述圖的例子:

圖的鄰接矩陣儲存法的空間複雜度為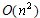 ,n為圖的頂點數。
,n為圖的頂點數。
2.鄰接表法
鄰接表是圖的鏈式儲存結構,對於圖G中的每個頂點vi,鄰接表法把所有鄰接於vi的頂點vj鏈成一個帶頭結點的單鏈表,這個單鏈表就是頂點vi的鄰接表,其頭結點描述了頂點vi資訊,其餘結點描述了與頂點vi相連的邊或弧的資訊。
(1)鄰接表的表結點結構
鄰接表中的每個結點代表了一條邊或弧,它由三個域組成,分別為:
① 鄰接點域adjvex
存放與vi相鄰接的頂點vj的序號j。
② 邊弧相關域info
存放與邊(vi,vj)或弧<vi,vj>相關的資訊,比如權值等。
③ 指標域next
指向單鏈表中下一結點的位置,也就是儲存下一條邊或弧的結點位置。
(2)頭結點結構
鄰接表的頭結點描述了頂點vi的資訊,它由兩個域組成,分別是:
① 頂點域data
存放頂點vi及其相關的資訊。
② 指標域first
記載vi的鄰接表的第一個結點的指標。
鄰接表的儲存結構示意如圖5-4所示。
為了便於隨機訪問任一頂點的鄰接表,一般情況需要將所有頭結點順序儲存在一個向量中。
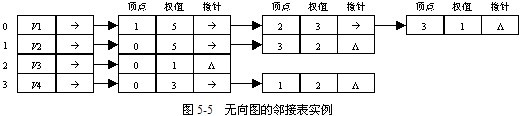
(3)無向圖的鄰接表
圖5-3(b)的無向圖鄰接表如圖5-5所示,其中頂點資訊用其向量下標來描述,本圖中增加了權值資訊,如果不需要儲存權值,可以不使用info域。
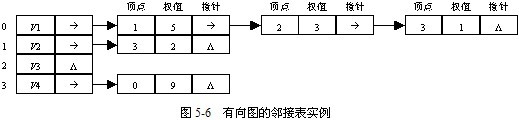
(4)有向圖的鄰接表
有向圖的鄰接表中儲存以vi為弧尾的弧資訊,圖5-3(a)的有向圖鄰接表如圖5-6所示。
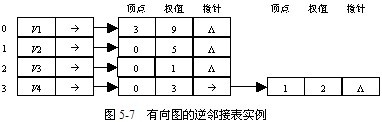
(5)有向圖的逆鄰接表
有向圖的鄰接表中儲存以vi為弧尾的弧資訊,現定義有向圖的逆鄰接表為:儲存每條以vi為弧頭的弧資訊,那麼圖5-3(a)的有向圖的逆鄰接表如圖5-7所示。
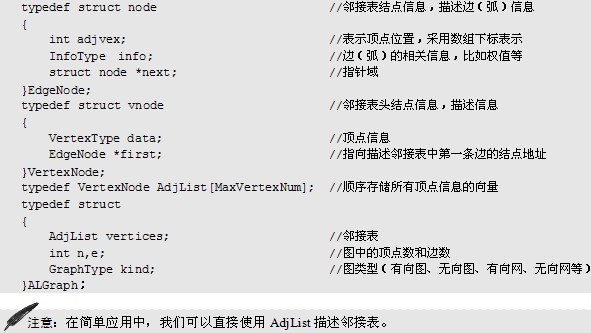
(6)鄰接表的儲存結構表示
如下定義了一個鄰接表描述圖的例子:
圖的鄰接表儲存法的空間複雜度為O(n+e),其中n為圖的頂點數,e為圖的邊數。
3.圖的兩種儲存結構比較
鄰接矩陣和鄰接表是圖的兩種最常用的儲存結構,它們各有特點,其比較如表5-2所示,其中n是圖的頂點數,e是圖的邊數(或弧數)。
表5-2 圖的鄰接矩陣儲存法與鄰接表儲存法特點比較
| 鄰接矩陣 |
鄰 接 表 |
|
| 儲存方式 | 順序儲存 | 鏈式儲存 |
| 描述方式 | 唯一 | 不唯一,各頂點鄰接表中的結點次序可以交換 |
| 空間複雜度 | O(n2) | O(n+e) |
| 附加資訊 | 儲存了不存在的邊的資訊 | 在每個表結點和頭結點中附加指標域 |
| 求無向圖頂點Vi度的演算法及其時間複雜度 | 演算法:統計第i行或第i列上的所有非0元素的個數 時間複雜度:O(n) |
演算法:統計頂點Vi鄰接表中的結點數,與圖的頂點數無關 最壞時間複雜度:O(e) 最好時間複雜度:O(1) |
| 求有向圖頂點Vi出度的演算法及其時間複雜度 | 演算法:統計第i行上的所有非0元素的個數 時間複雜度:O(n) |
演算法:統計頂點Vi鄰接表中的結點數,與圖的頂點數無關 最壞時間複雜度:O(e) 最好時間複雜度:O(1) |
| 求有向圖頂點Vi入度的演算法及其時間複雜度 | 演算法:統計第i列上的所有非0元素的個數 時間複雜度:O(n) |
演算法1:統計頂點Vi逆鄰接表中的結點數,與圖的頂點數無關 最壞時間複雜度:O(e) 最好時間複雜度:O(1) 演算法2:遍歷弧,統計全部頂點鄰接表中指向頂點Vi的結點 時間複雜度:O(n+e) |
| 求邊的數目的演算法及其時間複雜度 | 遍歷整個矩陣,無向圖為所有非0元素的個數的一半,有向圖為所有非0元素的個數 時間複雜度O(n2) |
遍歷所有頂點的鄰接表 時間複雜度:O(n+e) |
| 判斷頂點Vi和Vj之間是否存在邊或弧 | 判斷矩陣元素A[i,j]的取值,非0(圖)或非∞(網)則表示邊或弧存在 時間複雜度O(1) |
遍歷頂點Vi的鄰接表,無向圖需要再遍歷頂點Vj的鄰接表 最壞時間複雜度:O(e) 最好時間複雜度:O(1) |
總的來說,鄰接矩陣適用於稠密圖中,而鄰接表適用於稀疏圖中。
