人工智慧之機器學習主要有三大類：1）分類；2）迴歸；3）聚類。今天我們重點探討一下CART演算法。

　　我們知道十大機器學習中決策樹算法佔有兩席位置，即C4．5演算法和CART演算法，可見CART演算法的重要性。下面重點介紹CART演算法。

　　不同於ID3與C4．5，CART為一種二分決策樹，是滿二叉樹。CART演算法由Breiman等人在1984年提出，它採用與傳統統計學完全不同的方式構建預測準則，它是以二叉樹的形式給出，易於理解、使用和解釋。由CART模型構建的預測樹在很多情況下比常用的統計方法構建的代數學預測準則更加準確，且資料越複雜、變數越多，演算法的優越性就越顯著。

　　CART演算法既可用於分類也可用於迴歸。CART演算法被稱為資料探勘領域內里程碑式的演算法。

　**　CART演算法概念：**

　　CART（Classification andRegression Tree）分類迴歸樹是一種決策樹構建演算法。CART是在給定輸入隨機變數X條件下輸出隨機變數Y的條件概率分佈的學習方法。CART假設決策樹是二叉樹，內部結點特徵的取值為“是”和“否”，左分支是取值為“是”的分支，右分支是取值為“否”的分支。這樣的決策樹等價於遞迴地二分每個特徵，將輸入空間即特徵空間劃分為有限個單元，並在這些單元上確定預測的概率分佈，也就是在輸入給定的條件下輸出的條件概率分佈。

　　CART演算法既可以處理離散型問題，也可以處理連續型問題。這種演算法在處理連續型問題時，主要通過使用二元切分來處理連續型變數，即特徵值大於某個給定的值就走左子樹，或者就走右子樹。

**　　CART演算法組成：**

**　　CART演算法組成如下：**

　　1）決策樹生成：基於訓練資料集生成決策樹，生成的決策樹要儘量大；自上而下從根開始建立節點，在每個節點處要選擇一個最好（不同演算法使用不同指標來定義＂最好＂）的屬性來分裂，使得子節點中的訓練資料集儘量的純。

　　2）決策樹剪枝：用驗證資料集對已生成的樹進行剪枝並選擇最優子樹，這時損失函式最小作為剪枝的標準。這裡用代價複雜度剪枝CCP（Cost－Complexity Pruning）。

　　決策樹的生成就是通過遞迴地構建二叉決策樹的過程，對迴歸樹用平方誤差最小化準則，對分類樹用基尼指數最小化準則，進行特徵選擇，生成二叉樹。 　　CART決策樹生成：

　**　1）迴歸樹生成**

　　迴歸樹採用均方誤差作為損失函式，樹生成時會遞迴的按最優特徵與最優特徵下的最優取值對空間進行劃分，直到滿足停止條件為止，停止條件可以人為設定，比如當切分後的損失減小值小於給定的閾值ε，則停止切分，生成葉節點。對於生成的迴歸樹，每個葉節點的類別為落到該葉節點資料的標籤的均值。

　　迴歸樹為一棵二叉樹，每次都是按特徵下的某個取值進行劃分，每一個內部節點都是做一個對應特徵的判斷，直至走到葉節點得到其類別，構建這棵樹的難點在於如何選取最優的切分特徵與切分特徵對應的切分變數。

　　迴歸樹與模型樹既可以處理連續特徵也可以處理離散特徵。

　　迴歸樹生成演算法如下：

　　輸入：訓練資料集D＝｛（x1，y1），（x2，y2），…，（xN，yN）｝

　　輸出：迴歸樹T

　　1）求解選擇切分特徵j與切分特徵取值s，j將訓練集D劃分為兩部分，R1與R2，依照（j，s）切分後如下：

　　R1（j，s）＝｛xi｜xji≤s｝R2（j，s）＝｛xi｜xji＞s｝

　　c1＝1N1∑xi∈R1yi c2＝1N2∑xi∈R2yi

　　2）遍歷所有可能的解（j，s），找到最優的（j＊，s＊），最優的解使得對應損失最小，按照最優特徵（j＊，s＊）來切分即可。

　　Min｛∑（yi–c1）＾2＋∑（yi–c2）＾2｝

　　j，s xi∈R1 xi∈R2

　　3）遞迴呼叫1）和2），直到滿足停止條件。

　　4）返回決策樹T。

　　迴歸樹主要採用了分治策略，對於無法用唯一的全域性線性迴歸來優化的目標進行分而治之，進而取得比較準確的結果，但分段取均值並不是一個明智的選擇，可以考慮將葉節點設定為一個線性函式，這便是所謂的分段線性模型樹。實驗表明：模型樹效果比迴歸樹的效果要好一些。模型樹只需在迴歸樹的基礎上稍加修改即可，對於分到葉節點的資料，採用線性迴歸的最小均方損失來計算該節點的損失。　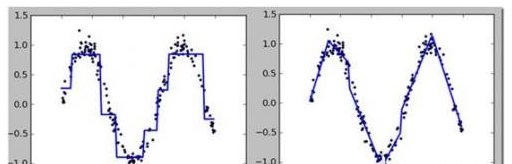　 　　2）分類樹生成

　　分類樹是CART中用來分類的，不同於ID3與C4．5，CART分類樹採用基尼指數來選擇最優的切分特徵，而且每次都是二分。

　　基尼指數是一個類似與熵的概念，對於一個有K種狀態對應的概率為p1，p2，…，pK的隨機變數X，其基尼指數Gini定義如下：

　　Gini（X）＝∑pk（1？pk）＝1？∑kp2k

　　k k

　　在已知特徵A條件下集合D的基尼指數：

　　Gini（D，A）＝（｜D1｜／｜D｜）＊Gini（D1）＋（｜D2｜／｜D｜）＊Gini（D2）

　　Gini（D，A）取值越大，樣本的不確定性也越大，這一點與熵類似，所以選擇特徵A的標準是Gini（D，A）的取值越小越好。