深度神經網路

摘要：深度學習是近年來計算機人工智慧領域非常火的研究方向，其相比傳統的淺層機器學習而言能夠挖掘出更多隱含的特徵。深度學習現如今已經廣泛的應用與計算機視覺、自然語言處理等領域，因此作為計算機專業人工智慧的學習者，學習和研究深度學習是一項必修課。
  神經網路作為作為深度學習的“常客”，是成為構建深度學習框架的主要結構，神經網路以其與人類神經元相類似的元素通過相互連線形成網路拓撲結構，而這種模型能夠自主挖掘更深層次特徵。

• 啟發：線性迴歸
• 神經網路的結構
• 神經網路的訓練
• 模型優化
• 其他經典的神經網路
• TensorFlow實現標準神經網路源程式
• 總結

一、啟發：線性迴歸

  神經網路的基本計算主要以線性和非線性為主，線性是為了對不同的特徵進行相互組合，其主要的運算結果是線性迴歸問題；非線性處理是為了對模型進行優化，使其能夠處理非線性問題，其主要運算以函式形式。
  線性模型是機器學習中最簡單的分類模型，單變數線性迴歸是典型的迴歸問題，其主要模型為：

$\hat{y}=$

W T x + b \hat y = W^Tx+b

其中 $W$

W 表示引數矩陣（或權重矩陣）， $b$ 表示偏向向量（一元線性曲線的截距）， $x$ 表示輸入的特徵向量， $\hat y$ 表示對應的輸出。線性分類器的目的便是訓練一個線性迴歸方程，使得其能夠擬合實際的樣本輸出。
通過曲線圖可以描繪線性迴歸方程的含義：
     
  下面給出模型訓練的推導：
  假設有一組訓練樣本，記作 $D=${( $X$, $Y$)| $X=${ $x_1,x_2,...,x_n$}, $Y=${ $y_1,y_2,...,y_n$}}，其中 $n$ 表示樣本數，選擇平方差作為損失函式，即：
$L(y,\hat y)=\frac{1}{2}|y-\hat y|^2$

則代價函式（所有樣本的損失函式的均值）為：
$J(Y,\hat Y)=\frac{1}{2n}\sum|y-\hat y|^2$

  構造了代價函式後，需要對其進行最優化處理，使得模型的代價儘可能降低。模型的優化方法常用的是梯度下降法（或稱最速下降法）。梯度下降法通過對需要優化調整的引數進行調參。線性迴歸模型中需要調整的引數有權重矩陣 $W$和偏向 $b$，因此需要對這些引數求偏導，以獲得梯度方向。
  Ps：梯度下降法需要鏈式法則完成偏導的求解。
  線性迴歸模型的梯度下降如下：
$\frac{\partial J}{\partial W^T}=\frac{\partial J}{\partial y^T}·\frac{\partial y^T}{\partial W^T}=\frac{1}{n}·(y-\hat y)·x$

$\frac{\partial J}{\partial b}=\frac{\partial J}{\partial y^T}·\frac{\partial y^T}{\partial b}=\frac{1}{n}·(y-\hat y)$

若選擇學習率為 $\alpha(0<\alpha<1)$，則引數調整為：
$W^T:W^T-\alpha\frac{\partial J}{\partial W^T}$

$b:b-\alpha\frac{\partial J}{\partial b}$

  通過不斷迴圈調參，直到引數變化非常小的時候（在程式設計過程中，可以設定一個變數用以判斷是否需要下一輪迭代），線性迴歸模型可以說訓練完成。在評估該模型時候，仍然可以使用損失函式來對測試集進行評估，並計算相應的準確率、召回率、F1值等。

二、神經網路的結構

  深入學習神經網路後會發，神經網路便是若干個線性迴歸方程的“相互交織”，再通過非線性方程進行“銳化”，因此第一節的線性迴歸問題是解決神經網路的基礎。
  神經網路是由神經元組成，神經元又稱資訊感知機，其通過多條路徑（突觸）接收外界資訊並傳導至神經細胞，並通過啟用或抑制等策略做出反應。這裡的突觸即為資料的輸入，神經細胞即為模型的結點，而反應即為啟用函式。模型圖如下所示：

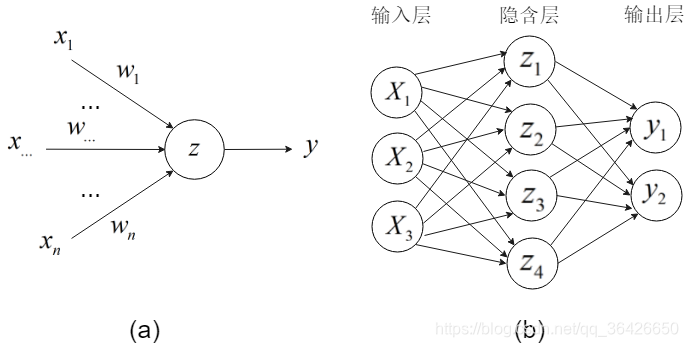
圖（a）為一個資訊感知機，輸入模型的資料為 $x_1,x_2,...,x_n$，連線的邊上的權重分別為 $w_1,w_2,...,w_n$ ，結點神經細胞獲取外界的輸入記為：
$ z = w 1 x 1 + w 2 x 2 + . . . 相關推薦 【火爐煉AI】深度學習003-構建並訓練深度神經網路模型 【火爐煉AI】深度學習003-構建並訓練深度神經網路模型 (本文所使用的Python庫和版本號: Python 3.6, Numpy 1.14, scikit-learn 0.19, matplotlib 2.2 ) 前面我們講解過單層神經網路模型，發現它結構簡單，難以解決一些實際的比較複雜的問題，故而現 #####好好好好####Keras深度神經網路訓練分類模型的四種方法 Github程式碼： Keras樣例解析 歡迎光臨我的部落格：https://gaussic.github.io/2017/03/03/imdb-sentiment-classification/ (轉載請註明出處：https://gaussic.github.io) Keras的官方E 估算深度神經網路的最優學習率 學習率如何影響訓練？ 深度學習模型通常由隨機梯度下降演算法進行訓練。隨機梯度下降演算法有許多變形：例如 Adam、RMSProp、Adagrad 等等。這些演算法都需要你設定學習率。學習率決定了在一個小批量（mini-batch）中權重在梯度方向要移動多遠。 如果學習率很低，訓練會變得更 深度學習資料整理（深度神經網路理解） https://blog.csdn.net/tiandijun/article/details/25192155   近這兩年裡deep learning技術在影象識別和跟蹤等方面有很大的突破，是一大研究熱點，裡面涉及的數學理論和應用技術很值得深入研究，這系列部落格總結了 深度神經網路的多工學習概覽(An Overview of Multi-task Learning in Deep Neural Networks) 譯自：http://sebastianruder.com/multi-task/ 1. 前言 在機器學習中，我們通常關心優化某一特定指標，不管這個指標是一個標準值，還是企業KPI。為了達到這個目標，我們訓練單一模型或多個模型集合來完成指定得任務。然後，我們通過精細調參，來改進模型直至效能不再 基於深度神經網路的說話人嵌入式端到端揚聲器驗證 DEEP NEURAL NETWORK-BASED SPEAKER EMBEDDINGS FOR END-TO-END SPEAKER VERIFICATION 基於深度神經網路的說話人嵌入式端到端揚聲器驗證   David Snyder *，Pegah Ghahremani， 一種利用語音深度神經網路進行語音識別的新方案 A NOVEL SCHEME FOR SPEAKER RECOGNITION USING A PHONETICALLY-AWARE DEEP NEURAL NETWORK Yun Lei Nicolas Scheffer Luciana Ferrer Mitchell McLaren 美國加 深度神經網路，適用於小型指令碼文字相關的語音驗證 DEEP NEURAL NETWORKS FOR SMALL FOOTPRINT TEXT-DEPENDENT SPEAKER VERIFICATION d-ivector系統優於i-ivector系統。 我們還嘗試了DNN培訓的不同配置。如果沒有maxo 【電腦科學】【2016】【含部分原始碼】深度神經網路及其實現 本文為捷克布拉格查理大學（作者：Bc. Ján Vojt）的碩士論文，共104頁。 深度神經網路是一種有效且通用的模型，能夠完成各種各樣的任務。本文主要研究了三種不同型別的深度神經網路——多層感知器、卷積神經網路和深度置信網路。所有討論的網路模型都是在並行硬體上實現的，並且針對網路 深度神經網路-keras-調參經驗 keras搬磚系列-調參經驗 1，觀察loss勝於觀察準確率，loss設計要比較合理，對比訓練集和驗證集的loss 2，relu可以很好的防止梯度彌散的問題，當然最後一層啟用函式儘量別用relu，如果分類則用softmax 3，BatchNorm 可以大大加快訓練速度和模型的 對基於深度神經網路的Auto Encoder用於異常檢測的一些思考 一、前言     現實中，大部分資料都是無標籤的，人和動物多數情況下都是通過無監督學習獲取概念，故而無監督學習擁有廣闊的業務場景。舉幾個場景：網路流量是正常流量還是攻擊流量、視訊中的人的行為是否正常、運維中伺服器狀態是否異常等等。有監督學習的做法是給樣本標出label，那麼標 基於深度神經網路的embeddding來構建推薦系統 在之前的部落格中，我主要介紹了embedding用於處理類別特徵的應用，其實，在學術界和工業界上，embedding的應用還有很多，比如在推薦系統中的應用。本篇部落格就介紹瞭如何利用embedding來構建一個圖書的推薦系統。 本文主要譯自《Building a Recommendation S 用深度神經網路搭建馬賽克神器，高清無碼效果感人 目錄 專案背景 適用範圍 使用方法 專案背景 相信一提起馬賽克這個東西，不少小夥伴都痛心疾首，雖然最近幾年也頻繁傳出有在研發去除馬賽克的軟體，一直沒有成品問世。不過最近一位程式設計師及經過不斷努力終於完成了這款軟體。 據悉這位程式設計師“deeppomf 神經網路6_CNN(卷積神經網路)、RNN(迴圈神經網路)、DNN(深度神經網路)概念區分理解  sklearn實戰-乳腺癌細胞資料探勘(部落格主親自錄製視訊教程，QQ：231469242) https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campaign=commission&utm 深度神經網路優化論文總結 1、HanS, Mao H, Dally W J. Deep Compression: Compressing Deep NeuralNetworks with Pruning, Trained Quantization and Huffman Coding[J].Fiber, 2015, 深度神經網路 深度神經網路 摘要：深度學習是近年來計算機人工智慧領域非常火的研究方向，其相比傳統的淺層機器學習而言能夠挖掘出更多隱含的特徵。深度學習現如今已經廣泛的應用與計算機視覺、自然語言處理等領域，因此作為計算機專業人工智慧的學習者，學習和研究深度學習是一項必修課。   神經網路作為作為深度學 最新深度神經網路演算法機器學習深度學系列 深度神經網路演算法機器學習深度學系列視訊教程 (基礎1)Python程式入門視訊 課程Python介紹_壓縮 環境配置 配置Python環境 以及資料型別 字串String和變數 資料型別2整型_字串 資料結構列表 列表List元組tuple對比 元組 詞典 函式 函式 控制流 控制流 控制流 控制 如何利用Keras中的權重約束減少深度神經網路中的過擬合                                           &nb 深度神經網路的計算 20180829 參考：https://www.nowcoder.com/courses/190 Error Error是一個直觀的計算方法，它計算了分類錯誤的資料點佔所有資料的比例，通常是對測試集中的資料進行測算。 Disadvantage 各個類別的資料不均衡的時候，產生 使用python實現深度神經網路 1 深度學習基本概念 一、實驗介紹 1.1 實驗內容 深度學習並沒有你想象的那麼難，本課程將會一邊講解深度學習中的基本理論，一邊通過動手使用python實現一個簡單的深度神經網路去驗證這些理論，讓你從原理上真正入門深度學習。 本次實驗將會帶大家學習深度學習中的一些最基本的概念，本次實驗很重要，理解這 $