PCB genesis Slot槽轉鑽孔(不用G85命令)實現方法
阿新 • • 發佈:2018-11-30
PCB鑽Slot槽一般都採用G85命令鑽槽孔,而採用G85命令工程CAM無法準確的知道Slot槽鑽多少個孔,並不能決定鑽槽孔的順序,因為採用G85命令鑽孔密度與鑽槽順序由鑽機本身決定的.在這裡介紹一種如果不用G85命令,如何將Slot槽生成多個鑽孔。
一.我們先了解一下G85命令鑽槽
鑽孔順序

孔密度
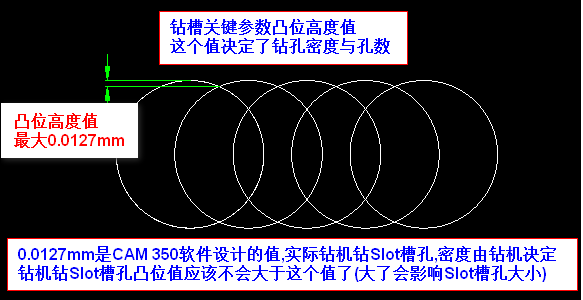
連一篇文章有關於Slot槽孔數計算方式: https://www.cnblogs.com/pcbren/p/9379178.html
二.求解思路
1.通過孔密度,求出孔與孔中心距離
2.再以Slot槽的一端做為起點,增量值(孔中心距),方位角(Slot槽的方位角),逐個求出下一個鑽孔位置.直到到達Slot槽終點節止。
三.C#簡易程式碼實現:
1.Slot槽轉鑽孔程式碼(這裡段程式碼實現將Slot槽轉為鑽孔,鑽孔順序是一個SLOT槽依次逐個從頭鑽到頭尾,和G85命令鑽槽順序不一樣)

string drilllayer = "drl"; gLayer layer = g.getFEATURES($"{drilllayer}", g.STEP, g.JOB, "View Codemm", true); List<gPP> pList = new List<gPP>(); foreach (var line in layer.Llist) { var HoleCenterDi = calc2.p_Convex(line.width * 0.0005); pList.AddRange(calc2.l_2Plist(line, HoleCenterDi, true)); } foreach(var arc in layer.Alist) { var HoleCenterDi = calc2.p_Convex(arc.width * 0.0005); pList.AddRange(calc2.a_2Plist(arc, HoleCenterDi,2, true)); } addCOM.pad(pList);
2.計算函式

/// <summary> /// 通過孔半徑與凸高位求 孔中心距 /// </summary> /// <param name="Rradius">孔半徑</param> /// <param name="tol_">凸位高度值</param> /// <returns></returns> public double p_Convex(double Rradius, double tol_ = 0.0127) { return Math.Sqrt(Math.Pow(Rradius, 2) - Math.Pow(Rradius - tol_, 2)) * 2; } /// <summary> /// 線Line 轉點P組集 /// </summary> /// <param name="l"></param> /// <param name="len_">點的間距</param> /// <returns></returns> public List<gPP> l_2Plist(gL l, double len_ = 0.1d, bool is_avg = false) { List<gPP> list_point = new List<gPP>();//採用優先佔用線兩端 如果有從線的一端出發增量間距後續再做更改 double line_len = l_Length(l); gPP tempP; tempP.p = l.ps; tempP.symbols = l.symbols; tempP.width = l.width; list_point.Add(tempP); int avg_count = (int)(Math.Ceiling(line_len / len_)) - 1; if (avg_count > 1) { if (is_avg) len_ = line_len / avg_count; double angle_ = p_ang(l.ps, l.pe); for (int i = 0; i < avg_count; i++) { tempP = p_val_ang(tempP, len_, angle_); list_point.Add(tempP); } } tempP.p = l.pe; list_point.Add(tempP); return list_point; } /// <summary> /// 求方位角 /// </summary> /// <param name="ps"></param> /// <param name="pe"></param> /// <returns></returns> public double p_ang(gPoint ps, gPoint pe) { double a_ang = Math.Atan((pe.y - ps.y) / (pe.x - ps.x)) / Math.PI * 180; //象限角 轉方位角 計算所屬象限 並求得方位角 if (pe.x >= ps.x && pe.y >= ps.y) //↗ 第一象限 { return a_ang; } else if (!(pe.x >= ps.x) && pe.y >= ps.y) // ↖ 第二象限 { return a_ang + 180; } else if (!(pe.x >= ps.x) && !(pe.y >= ps.y)) //↙ 第三象限 { return a_ang + 180; } else if (pe.x >= ps.x && !(pe.y >= ps.y)) // ↘ 第四象限 { return a_ang + 360; } else { return a_ang; } }//求方位角 /// <summary> /// 求增量座標 /// </summary> /// <param name="ps">起點</param> /// <param name="val">增量值</param> /// <param name="ang_direction">角度</param> /// <returns></returns> public gPP p_val_ang(gPP ps, double val, double ang_direction) { gPP pe = ps; pe.p.x = ps.p.x + val * Math.Cos(ang_direction * Math.PI / 180); pe.p.y = ps.p.y + val * Math.Sin(ang_direction * Math.PI / 180); return pe; } /// <summary> /// 求線Line長度 /// </summary> /// <param name="l"></param> /// <param name="is_calc_width"></param> /// <returns></returns> public double l_Length(gL l, bool is_calc_width = false) { if (is_calc_width) return Math.Sqrt((l.ps.x - l.pe.x) * (l.ps.x - l.pe.x) + (l.ps.y - l.pe.y) * (l.ps.y - l.pe.y)) + l.width / 1000; else return Math.Sqrt((l.ps.x - l.pe.x) * (l.ps.x - l.pe.x) + (l.ps.y - l.pe.y) * (l.ps.y - l.pe.y)); } /// <summary> /// 弧Arc 轉點P組集 /// </summary> /// <param name="a"></param> /// <param name="val_">此數值表示:分段數值</param> /// <param name="type_">代表值數值型別 【0】弧長 【1】角度 【2】弦長 </param> /// <param name="is_avg">是否平均分佈 </param> /// <returns></returns> public List<gPP> a_2Plist(gA a, double val_ = 0.1d, int type_ = 0, bool is_avg = false) { List<gPP> list_point = new List<gPP>(); gPP tempP; tempP.p = a.ps; tempP.symbols = a.symbols; tempP.width = a.width; list_point.Add(tempP); double avg_count; double angle_val = 0; double rad_ = p2p_di(a.pc, a.pe); double sum_alge = a_Angle(a); if (type_ == 1) // 【1】角度 { angle_val = val_; avg_count = (int)(Math.Ceiling(sum_alge / angle_val)) - 1; // 總角度/單角度 } else if (type_ == 2) //【2】弦長 { angle_val = Math.Asin(val_ / (rad_ * 2)) * 360 / pi; avg_count = (int)(Math.Ceiling(sum_alge / angle_val)) - 1; // 總角度/單角度 } else // 【0】弧長 { angle_val = val_ * 180 / (pi * rad_); avg_count = (int)(Math.Ceiling(sum_alge / angle_val)) - 1; // 總角度/單角度 //avg_count = (int)(Math.Ceiling(a_Lenght(a) / val_)) - 1; // 或 總弧長/單弧長 } if (is_avg) angle_val = sum_alge / avg_count; if (avg_count > 1) { gPP centerP = tempP; centerP.p = a.pc; double angle_s = p_ang(a.pc, a.ps); if (a.ccw) { angle_val = 0 - angle_val; } for (int i = 1; i < avg_count; i++) { tempP = p_val_ang(centerP, rad_, angle_s - angle_val * i); list_point.Add(tempP); } } if (!(zero(a.ps.x - a.pe.x) && zero(a.ps.y - a.pe.y))) { tempP.p = a.pe; list_point.Add(tempP); } return list_point; } /// <summary> /// 返回兩點之間歐氏距離 /// </summary> /// <param name="p1"></param> /// <param name="p2"></param> /// <returns></returns> public double p2p_di(gPoint p1, gPoint p2) { return Math.Sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y)); } /// <summary> /// 求弧Arc圓心角 //後續改進 用叉積 與3P求角度求解 驗證哪個效率高 /// </summary> /// <param name="a"></param> /// <returns></returns> public double a_Angle(gA a) { double angle_s, angle_e, angle_sum; if (a.ccw) { angle_s = p_ang(a.pc, a.pe); angle_e = p_ang(a.pc, a.ps); } else { angle_s = p_ang(a.pc, a.ps); angle_e = p_ang(a.pc, a.pe); } if (angle_s == 360) { angle_s = 0; } if (angle_e >= angle_s) angle_sum = 360 - Math.Abs(angle_s - angle_e); else angle_sum = Math.Abs(angle_s - angle_e); return angle_sum; }View Code
3.Point,PAD,Line,Arc資料結構

/// <summary> /// 精簡 PAD 資料型別 /// </summary> public struct gPP { public gPP(double x_val, double y_val, double width_) { this.p = new gPoint(x_val, y_val); this.symbols = "r"; this.width = width_; } public gPP(gPoint p_, double width_) { this.p = p_; this.symbols = "r"; this.width = width_; } public gPP(gPoint p_, string symbols_, double width_) { this.p = p_; this.symbols = symbols_; this.width = width_; } public gPoint p; public string symbols; public double width; public static gPP operator +(gPP p1, gPP p2) { p1.p += p2.p; return p1; } public static gPP operator +(gPP p1, gPoint p2) { p1.p += p2; return p1; } public static gPP operator -(gPP p1, gPP p2) { p1.p -= p2.p; return p1; } public static gPP operator -(gPP p1, gPoint p2) { p1.p -= p2; return p1; } } /// <summary> /// 點 資料型別 (XY) /// </summary> public struct gPoint { public gPoint(gPoint p_) { this.x = p_.x; this.y = p_.y; } public gPoint(double x_val, double y_val) { this.x = x_val; this.y = y_val; } public double x; public double y; public static gPoint operator +(gPoint p1, gPoint p2) { p1.x += p2.x; p1.y += p2.y; return p1; } public static gPoint operator -(gPoint p1, gPoint p2) { p1.x -= p2.x; p1.y -= p2.y; return p1; } } /// <summary> /// Line 資料型別 /// </summary> public struct gL { public gL(double ps_x, double ps_y, double pe_x, double pe_y, double width_) { this.ps = new gPoint(ps_x, ps_y); this.pe = new gPoint(pe_x, pe_y); this.negative = false; this.symbols = "r"; this.attribut = string.Empty; this.width = width_; } public gL(gPoint ps_, gPoint pe_, double width_) { this.ps = ps_; this.pe = pe_; this.negative = false; this.symbols = "r"; this.attribut = string.Empty; this.width = width_; } public gL(gPoint ps_, gPoint pe_, string symbols_, double width_) { this.ps = ps_; this.pe = pe_; this.negative = false; this.symbols = symbols_; this.attribut = string.Empty; this.width = width_; } public gPoint ps; public gPoint pe; public bool negative;//polarity-- positive negative public string symbols; public string attribut; public double width; public static gL operator +(gL l1, gPoint move_p) { l1.ps += move_p; l1.pe += move_p; return l1; } public static gL operator +(gL l1, gP move_p) { l1.ps += move_p.p; l1.pe += move_p.p; return l1; } public static gL operator -(gL l1, gPoint move_p) { l1.ps -= move_p; l1.pe -= move_p; return l1; } public static gL operator -(gL l1, gP move_p) { l1.ps -= move_p.p; l1.pe -= move_p.p; return l1; } } /// <summary> /// ARC 資料型別 /// </summary> public struct gA { public gA(double ps_x, double ps_y, double pc_x, double pc_y, double pe_x, double pe_y, double width_, bool ccw_) { this.ps = new gPoint(ps_x, ps_y); this.pc = new gPoint(pc_x, pc_y); this.pe = new gPoint(pe_x, pe_y); this.negative = false; this.ccw = ccw_; this.symbols = "r"; this.attribut = string.Empty; this.width = width_; } public gA(gPoint ps_, gPoint pc_, gPoint pe_, double width_, bool ccw_ = false) { this.ps = ps_; this.pc = pc_; this.pe = pe_; this.negative = false; this.ccw = ccw_; this.symbols = "r"; this.attribut = string.Empty; this.width = width_; } public gPoint ps; public gPoint pe; public gPoint pc; public bool negative;//polarity-- positive negative public bool ccw; //direction-- cw ccw public string symbols; public string attribut; public double width; public static gA operator +(gA arc1, gPoint move_p) { arc1.ps += move_p; arc1.pe += move_p; arc1.pc += move_p; return arc1; } public static gA operator +(gA arc1, gP move_p) { arc1.ps += move_p.p; arc1.pe += move_p.p; arc1.pc += move_p.p; return arc1; } public static gA operator -(gA arc1, gPoint move_p) { arc1.ps -= move_p; arc1.pe -= move_p; arc1.pc -= move_p; return arc1; } public static gA operator -(gA arc1, gP move_p) { arc1.ps -= move_p.p; arc1.pe -= move_p.p; arc1.pc -= move_p.p; return arc1; } }View Code
四.實現效果


