PCB genesis連孔加除毛刺孔(圓孔與槽孔)實現方法(二)
阿新 • • 發佈:2018-11-17
一.為什麼 連孔加除毛刺孔
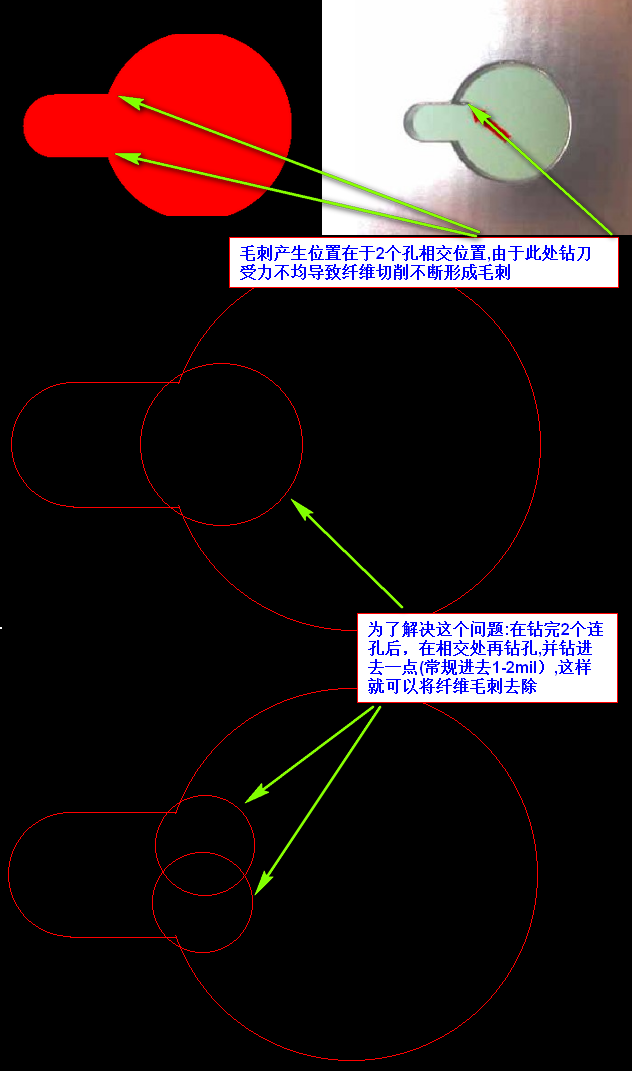
原因是 PCB板材中含有玻璃纖維, 毛刺產生位置在於2個孔相交位置,由於此處鑽刀受力不均導致纖維切削不斷形成毛刺 ,為了解決這個問題:在鑽完2個連孔後,在相交處再鑽一個孔,並鑽進去一點(常規進去1-2mil),這樣就可以將纖維毛刺去除
PCB同行業毛刺問題處理辦法 鑽孔孔內毛刺問題分析改善報告
二.如何判斷除毛刺孔是加1個還是2個呢?
在PCB行業工程加除毛刺孔是加1個孔還是2個孔,沒有太明確的定義,只要滿足毛刺去除即可.
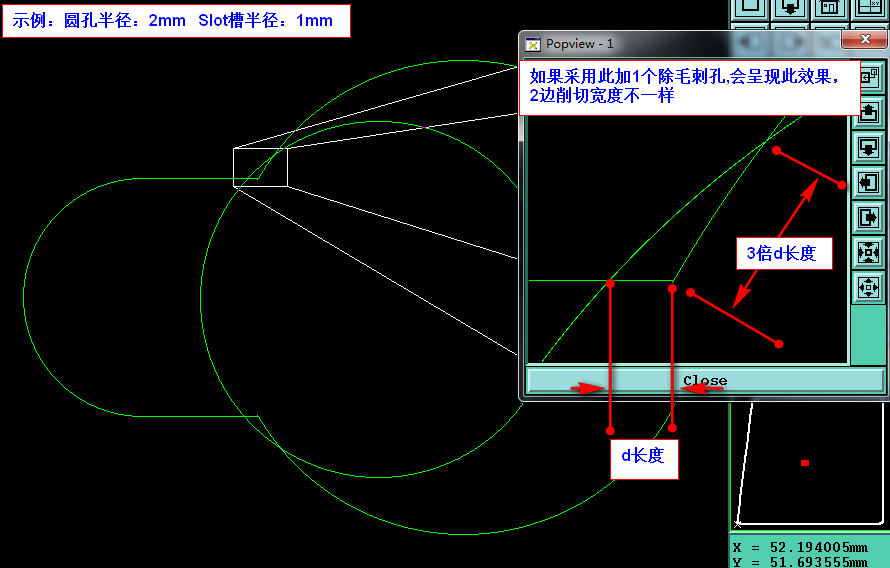
我們先看下面這個示例(採用此加1個除毛刺孔,會呈現此效果,2邊削切寬度不一樣)為了防止此切削寬度不一致現象,所以需採用增加2個除毛刺孔。
這邊測試後得出一個判斷條件(但不一定適合所有工廠),加1個除毛刺孔條件需滿足: (1.槽半徑小於三分之二大圓半徑時,增加1個毛刺孔 2.槽寬>=0.8mm,增加1個毛刺孔),否則需加2個毛刺孔
三.連孔加除毛刺孔實現原理
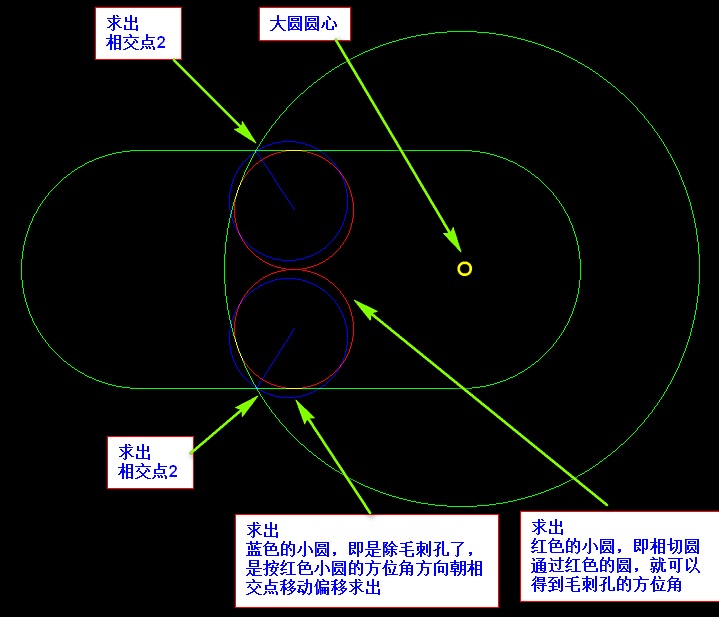
除毛刺孔,這裡列舉幾個關鍵引數,如下圖所示(因為求解的引數太多,畫圖不好呈現,具體請看下方的程式碼)
1.加1 個孔

2.加2個孔
四.C#簡易程式碼實現:
1.加除毛刺孔程式碼

#region 加除毛刺孔 mcdrl gLayer glayer = g.getFEATURES($"{"drl"}", g.STEP, g.JOB, "mm", true); gP hole = glayer.Plist[0]; gL line = glayer.Llist[0]; gA arcView Code= calc2.p_2A(hole); List<gP> gpList = calc2.l2a_IntersectHole(line, arc,1.3,0.076); addCOM.pad(gpList); #endregion
2.計算函式

/// <summary> /// 求線段與弧2個交點 /// </summary> /// <param name="L1"></param> /// <param name="L2"></param> /// <param name="HoleScale">當加1個孔時 是開口寬度1.3倍</param> /// <param name="CutInner">切入板內0.05mm</param> /// <returns></returns> public List<gP> l2a_IntersectHole(gL l, gA a, double HoleScale = 1.3, double CutInner = 0.05) { List<gP> gpList = new List<gP>(); double Lwidth = l.width * 0.001; gL lineL, lineR; l_offset(l, Lwidth * 0.5, out lineL, out lineR); gPoint gpL = new gPoint(); gPoint gpR = new gPoint(); int isIntersectL = 0, isIntersectR = 0; double A_Radius = p2p_di(a.pc, a.ps); gL l1 = l2a_Intersect(lineL, a, ref gpL, ref isIntersectL); gL l2 = l2a_Intersect(lineR, a, ref gpR, ref isIntersectR); gL gpL1 = new gL(l1.ps, l2.ps, 100); double gpL1di = l_Length(gpL1); gL gpL2 = new gL(l1.pe, l2.pe, 100); double gpL2di = l_Length(gpL2); if (isIntersectL + isIntersectR < 2) gpL1di = 1000; //鑽1個孔條件 if (gpL1di < A_Radius * 0.667 && gpL1di >= 0.8) //當小於Slot槽寬要小於0.667倍大圓半徑,且Slot槽需大於0.8 { if (p2p_di(lineL.ps, a.pc) >= A_Radius && p2p_di(lineR.ps, a.pc) >= A_Radius) { double Hole_Radius = ((int)(Math.Ceiling(((gpL1di + CutInner) * HoleScale * 1000) / 50)) * 50) * 0.0005; gP gpL1P = l2a_CentereExtend(gpL1, a, Hole_Radius - CutInner); gpList.Add(new gP(gpL1P.p, (Hole_Radius) * 2000)); } if (p2p_di(lineL.pe, a.pc) >= A_Radius && p2p_di(lineR.pe, a.pc) >= A_Radius) { double Hole_Radius = ((int)(Math.Ceiling(((gpL2di + CutInner) * HoleScale * 1000) / 50)) * 50) * 0.0005; gP gpL2P = l2a_CentereExtend(gpL2, a, Hole_Radius - CutInner); gpList.Add(new gP(gpL2P.p, (Hole_Radius) * 2000)); } } else //鑽2個孔 { double Radius = (isIntersectL + isIntersectR < 2) ? Lwidth * 0.5 : gpL1di * 0.5; double multiLval = multi(lineL.ps, lineL.pe, a.pc); double multiRval = multi(lineR.ps, lineR.pe, a.pc); bool isSameSide = (multiLval >= 0 && multiRval >= 0) || (multiLval <= 0 && multiRval <= 0); int line1L_Position = 1, line1R_Position = 1; ; if (isSameSide) { if (Math.Abs(multiLval) > Math.Abs(multiRval)) line1R_Position = 4; else line1L_Position = 4; } if (isIntersectL == 1) { gL_di line1L = l2a__Round(lineL, a, 0.05, 0.5, 1, line1L_Position); if (line1L.isIntersect) { gPoint pointLP1 = p_val_ang(line1L.pc, Radius - CutInner, line1L.ang_direction); gpList.Add(new gP(pointLP1, Radius * 2000)); } gL_di line1R = l2a__Round(lineL, a, 0.05, 0.5, 2, line1L_Position); if (line1R.isIntersect) { gPoint pointLP2 = p_val_ang(line1R.pc, Radius - CutInner, line1R.ang_direction); gpList.Add(new gP(pointLP2, Radius * 2000)); } } if (isIntersectR == 1) { gL_di line2L = l2a__Round(lineR, a, 0.05, 0.5, 1, line1R_Position); if (line2L.isIntersect) { gPoint pointRP3 = p_val_ang(line2L.pc, Radius - CutInner, line2L.ang_direction); gpList.Add(new gP(pointRP3, Radius * 2000)); } gL_di line2R = l2a__Round(lineR, a, 0.05, 0.5, 2, line1R_Position); if (line2R.isIntersect) { gPoint pointRP4 = p_val_ang(line2R.pc, Radius - CutInner, line2R.ang_direction); gpList.Add(new gP(pointRP4, Radius * 2000)); } } } return gpList; } /// <summary> /// 線Line偏移 out 左與右偏移線Line /// </summary> /// <param name="l"></param> /// <param name="offset_val">偏移數值</param> /// <param name="left_l">out 左偏移線L</param> /// <param name="rithg_l">out 右偏移線L</param> public void l_offset(gL l, double offset_val, out gL left_l, out gL rithg_l) { left_l = l; rithg_l = l; double angle_ = p_ang(l.ps, l.pe); left_l.ps = p_val_ang(l.ps, offset_val, angle_ + 90); left_l.pe = p_val_ang(l.pe, offset_val, angle_ + 90); rithg_l.ps = p_val_ang(l.ps, offset_val, angle_ - 90); rithg_l.pe = p_val_ang(l.pe, offset_val, angle_ - 90); } /// <summary> /// 返回兩點之間歐氏距離 /// </summary> /// <param name="p1"></param> /// <param name="p2"></param> /// <returns></returns> public double p2p_di(gPoint p1, gPoint p2) { return Math.Sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y)); } /// <summary> /// 求線段與弧2個交點 /// </summary> /// <param name="l"></param> /// <param name="a"></param> /// <param name="gp">垂足</param> /// <param name="isIntersectType">1本身相交 0本身不相交 (相對於圓而言)</param> /// <returns></returns> public gL l2a_Intersect(gL l, gA a, ref gPoint gp, ref int isIntersectType) { gp = p2l_toP(a.pc, l); double pc2gpDi = p2p_di(gp, a.pc); double Radius = p2p_di(a.pc, a.ps); isIntersectType = Radius >= pc2gpDi ? 1 : 0; double val = Math.Sqrt(Math.Pow(Radius, 2) - Math.Pow(pc2gpDi, 2)); double ang = p_ang(gp, l.ps); bool isIsNaN = false; if (double.IsNaN(ang)) { isIsNaN = true; ang = p_ang(gp, l.pe); } gPoint leftP = p_val_ang(gp, val, ang); gPoint rightP = p_val_ang(gp, val, ang - 180); if (isIsNaN) return new gL(rightP, leftP, 100); else return new gL(leftP, rightP, 100); } /// <summary> /// 求線Line長度 /// </summary> /// <param name="l"></param> /// <param name="is_calc_width"></param> /// <returns></returns> public double l_Length(gL l, bool is_calc_width = false) { if (is_calc_width) return Math.Sqrt((l.ps.x - l.pe.x) * (l.ps.x - l.pe.x) + (l.ps.y - l.pe.y) * (l.ps.y - l.pe.y)) + l.width / 1000; else return Math.Sqrt((l.ps.x - l.pe.x) * (l.ps.x - l.pe.x) + (l.ps.y - l.pe.y) * (l.ps.y - l.pe.y)); } /// <summary> /// 求叉積 判斷【點P與線L】位置關係【小於0】在右邊 【大於0】在左邊 【等於0】共線 /// </summary> /// <param name="ps"></param> /// <param name="pe"></param> /// <param name="p"></param> /// <returns>【小於0】在右邊 【大於0】在左邊 【等於0】共線</returns> public double multi(gPoint ps, gPoint pe, gPoint p) { return ((ps.x - p.x) * (pe.y - p.y) - (pe.x - p.x) * (ps.y - p.y)); } /// <summary> /// 求線段與弧段倒圓角 //2個交點時處理 相交時檢測最近點所有位置 孔大於開口處理 孔小於開口處理 /// </summary> /// <param name="l"></param> /// <param name="a"></param> /// <param name="Radius">內角孔 半徑 </param> /// <param name="tolerance">連線位公差 暫先忽略</param> /// <param name="l2aType">【0】 自動選取最近點 【1】左(垂足點到PC) 【2】右(垂足點到PC) </param> /// <param name="l2aPosition">【0】 自動選取最長線段為夾角 【1】圓內,近芯 【2】圓外,近芯 【3】圓外,遠芯 【4】圓內,遠芯 </param> /// <returns></returns> public gL_di l2a__Round(gL l, gA a, double Radius, double tolerance = 0.5, int l2aTypeLR = 0, int l2aPosition = 0) { gL_di gldi = new gL_di(); d1 calc1 = new d1(); gPoint gp = p2l_toP(a.pc, l); double ang = p_ang(gp, a.pc); double aRdi = p2p_di(a.pc, a.ps); double gp2pcDi = p2p_di(gp, a.pc); gPoint gpMin = new gPoint(); //由於會產生2個交點,取最近一個交點 double val = 0; //弦長 的一半 bool isDisjoint = false; if (aRdi > gp2pcDi) //線在弧內 { //求交點 val = Math.Sqrt(Math.Pow(p2p_di(a.pc, a.ps), 2) - Math.Pow(p2p_di(gp, a.pc), 2)); gPoint leftP = p_val_ang(gp, val, ang + 90); gPoint rightP = p_val_ang(gp, val, ang - 90); //sxi 2018-9-11 此判斷通地最近距離判斷最近交點 不太準確,後續修正 if (l2aTypeLR == 1) gpMin = leftP; else if (l2aTypeLR == 2) gpMin = rightP; else { if ((p2p_di(leftP, a.ps) + p2p_di(leftP, a.pe) > p2p_di(rightP, a.ps) + p2p_di(rightP, a.pe))) { gpMin = rightP; l2aTypeLR = 2; } else { gpMin = leftP; l2aTypeLR = 1; } } } else//線在弧外 { isDisjoint = true; gpMin = gp; if (multi(gp, a.pc, l.ps) + multi(gp, a.pc, l.pe) > 0) { l2aTypeLR = 1; } else { l2aTypeLR = 2; } } gldi.pc = gpMin; int Lindex = p2p_di_minP(gpMin, l.ps, l.pe); int Aindex = p2p_di_minP(gpMin, a.ps, a.pe); if (Lindex == 0) { gldi.p1 = l.ps; gldi.p1_Ptype = Ptype.ps; } else if (Lindex == 1) { gldi.p1 = l.pe; gldi.p1_Ptype = Ptype.pe; } if (Aindex == 0) { gldi.p2 = a.ps; gldi.p2_Ptype = Ptype.ps; } else if (Aindex == 1) { gldi.p2 = a.pe; gldi.p2_Ptype = Ptype.pe; } if (l2aPosition == 0) l2aPosition = 1; //求弧 if (!isDisjoint) //線在弧內 { if (l2aPosition == 1) // 左上↖ val = Math.Sqrt(Math.Pow(p2p_di(a.pc, a.ps) - Radius, 2) - Math.Pow(p2p_di(gp, a.pc) - Radius, 2)); else if (l2aPosition == 2) //右上↗ val = Math.Sqrt(Math.Pow(p2p_di(a.pc, a.ps) + Radius, 2) - Math.Pow(p2p_di(gp, a.pc) - Radius, 2)); else if (l2aPosition == 3) //右下↘ val = Math.Sqrt(Math.Pow(p2p_di(a.pc, a.ps) + Radius, 2) - Math.Pow(p2p_di(gp, a.pc) + Radius, 2)); else if (l2aPosition == 4) //左下↙ val = Math.Sqrt(Math.Pow(p2p_di(a.pc, a.ps) - Radius, 2) - Math.Pow(p2p_di(gp, a.pc) + Radius, 2)); } else { val = Math.Sqrt(Math.Pow(p2p_di(a.pc, a.ps) + Radius, 2) - Math.Pow(p2p_di(gp, a.pc) - Radius, 2)); l2aPosition = 1; } double angTB = ang; gL gl; if ((l2aPosition == 3) || (l2aPosition == 4)) //線外 { angTB = p_ang_invert(ang); gl = p_val_angL(gp, Radius, angTB, val * 2); gPoint gpTemp = gl.ps; gl.ps = gl.pe; gl.pe = gpTemp; } else { gl = p_val_angL(gp, Radius, angTB, val * 2); } gPoint gpPc = (l2aTypeLR == 2) ? gl.pe : gl.ps; double angL = p_ang(a.pc, gpPc); if ((l2aPosition == 2) || (l2aPosition == 3) || isDisjoint) //圓外 { angL = p_ang_invert(angL); } gA ga = new gA(); ga.pc = gpPc; if (l2aTypeLR == 2) //右 { gPoint maxP = multi(gp, a.pc, l.ps) < multi(gp, a.pc, l.pe) ? l.ps : l.pe; double lineRdi = p2p_di(a.pc, maxP); gldi.isIntersect = lineRdi > aRdi; //不包含線在圓外檢測判斷 if (((l2aPosition == 1) || (l2aPosition == 3)) && !isDisjoint) { ga.ps = p_val_ang(gpPc, Radius, angL);//弧切點 ga.pe = p_val_ang(gp, val, ang - 90);//線切點 } else { ga.ps = p_val_ang(gp, val, ang - 90);//線切點 ga.pe = p_val_ang(gpPc, Radius, angL);//弧切點 } } else if (l2aTypeLR == 1)//左 { gPoint maxP = multi(gp, a.pc, l.ps) > multi(gp, a.pc, l.pe) ? l.ps : l.pe; double lineRdi = p2p_di(a.pc, maxP); gldi.isIntersect = lineRdi > aRdi;//不包含線在圓外檢測判斷 if (((l2aPosition == 1) || (l2aPosition == 3)) && !isDisjoint) { ga.ps = p_val_ang(gp, val, ang + 90); //線切點 ga.pe = p_val_ang(gpPc, Radius, angL);//弧切點 } else { ga.ps = p_val_ang(gpPc, Radius, angL);//弧切點 ga.pe = p_val_ang(gp, val, ang + 90); //線切點 } } gldi.a = ga; gldi.State = 1; ; //線段 目前僅支援:線在弧內,弧段與線間距不檢測 return gldi; } /// <summary> /// 求增量座標 /// </summary> /// <param name="ps">起點</param> /// <param name="val">增量值</param> /// <param name="ang_direction">角度</param> /// <returns></returns> public gPoint p_val_ang(gPoint ps, double val, double ang_direction) { gPoint pe; pe.x = ps.x + val * Math.Cos(ang_direction * Math.PI / 180); pe.y = ps.y + val * Math.Sin(ang_direction * Math.PI / 180); return pe; } /// <summary> /// 弦長不變,更新新圓半徑,並求出新圓中心點 /// </summary> /// <param name="l">弦長</param> /// <param name="a">圓弧</param> /// <param name="Cval">新圓半徑</param> /// <returns></returns> public gP l2a_CentereExtend(gL l, gA a, double Cval) { double gpdi = l_Length(l); gPoint gpcenter = l_centerP(l); double gpang = p_ang(gpcenter, a.pc); double A_Radius = p2p_di(a.pc, a.ps); double Bval = (gpdi * 0.5); double Aval = Math.Sqrt(Cval * Cval - Bval * Bval); gPoint gpPoint = p_val_ang(gpcenter, Aval, gpang); return new gP(gpPoint, Cval * 2000); }View Code
3.Point,PAD;Line;Arc資料結構

/// <summary> /// Line 資料型別 /// </summary> public struct gL { public gL(double ps_x, double ps_y, double pe_x, double pe_y, double width_) { this.ps = new gPoint(ps_x, ps_y); this.pe = new gPoint(pe_x, pe_y); this.negative = false; this.symbols = "r"; this.attribut = string.Empty; this.width = width_; } public gL(gPoint ps_, gPoint pe_, double width_) { this.ps = ps_; this.pe = pe_; this.negative = false; this.symbols = "r"; this.attribut = string.Empty; this.width = width_; } public gL(gPoint ps_, gPoint pe_, string symbols_, double width_) { this.ps = ps_; this.pe = pe_; this.negative = false; this.symbols = symbols_; this.attribut = string.Empty; this.width = width_; } public gPoint ps; public gPoint pe; public bool negative;//polarity-- positive negative public string symbols; public string attribut; public double width; public static gL operator +(gL l1, gPoint move_p) { l1.ps += move_p; l1.pe += move_p; return l1; } public static gL operator +(gL l1, gP move_p) { l1.ps += move_p.p; l1.pe += move_p.p; return l1; } public static gL operator -(gL l1, gPoint move_p) { l1.ps -= move_p; l1.pe -= move_p; return l1; } public static gL operator -(gL l1, gP move_p) { l1.ps -= move_p.p; l1.pe -= move_p.p; return l1; } } /// <summary> /// ARC 資料型別 /// </summary> public struct gA { public gA(double ps_x, double ps_y, double pc_x, double pc_y, double pe_x, double pe_y, double width_, bool ccw_) { this.ps = new gPoint(ps_x, ps_y); this.pc = new gPoint(pc_x, pc_y); this.pe = new gPoint(pe_x, pe_y); this.negative = false; this.ccw = ccw_; this.symbols = "r"; this.attribut = string.Empty; this.width = width_; } public gA(gPoint ps_, gPoint pc_, gPoint pe_, double width_, bool ccw_ = false) { this.ps = ps_; this.pc = pc_; this.pe = pe_; this.negative = false; this.ccw = ccw_; this.symbols = "r"; this.attribut = string.Empty; this.width = width_; } public gPoint ps; public gPoint pe; public gPoint pc; public bool negative;//polarity-- positive negative public bool ccw; //direction-- cw ccw public string symbols; public string attribut; public double width; public static gA operator +(gA arc1, gPoint move_p) { arc1.ps += move_p; arc1.pe += move_p; arc1.pc += move_p; return arc1; } public static gA operator +(gA arc1, gP move_p) { arc1.ps += move_p.p; arc1.pe += move_p.p; arc1.pc += move_p.p; return arc1; } public static gA operator -(gA arc1, gPoint move_p) { arc1.ps -= move_p; arc1.pe -= move_p; arc1.pc -= move_p; return arc1; } public static gA operator -(gA arc1, gP move_p) { arc1.ps -= move_p.p; arc1.pe -= move_p.p; arc1.pc -= move_p.p; return arc1; } } /// <summary> /// PAD 資料型別 /// </summary> public struct gP { public gP(double x_val, double y_val, double width_) { this.p = new gPoint(x_val, y_val); this.negative = false; this.angle = 0; this.mirror = false; this.symbols = "r"; this.attribut = string.Empty; this.width = width_; } public gPoint p; public bool negative;//polarity-- positive negative public double angle; public bool mirror; public string symbols; public string attribut; public double width; public static gP operator +(gP p1, gP p2) { p1.p += p2.p; return p1; } public static gP operator -(gP p1, gP p2) { p1.p -= p2.p; return p1; } } /// <summary> /// 點 資料型別 (XY) /// </summary> public struct gPoint { public gPoint(gPoint p_) { this.x = p_.x; this.y = p_.y; } public gPoint(double x_val, double y_val) { this.x = x_val; this.y = y_val; } public double x; public double y; public static gPoint operator +(gPoint p1, gPoint p2) { p1.x += p2.x; p1.y += p2.y; return p1; } public static gPoint operator -(gPoint p1, gPoint p2) { p1.x -= p2.x; p1.y -= p2.y; return p1; } }View Code
五.在Genesis或Incam中如何判斷是否為連孔
判斷2個孔是否為連孔,可以自己寫演算法實現啦,當然更多人還是會選擇奧寶提供DrillChecklist分析出來的的結果來判斷是否為連孔.因為你自己寫的演算法效率沒有奧寶的效率高呀


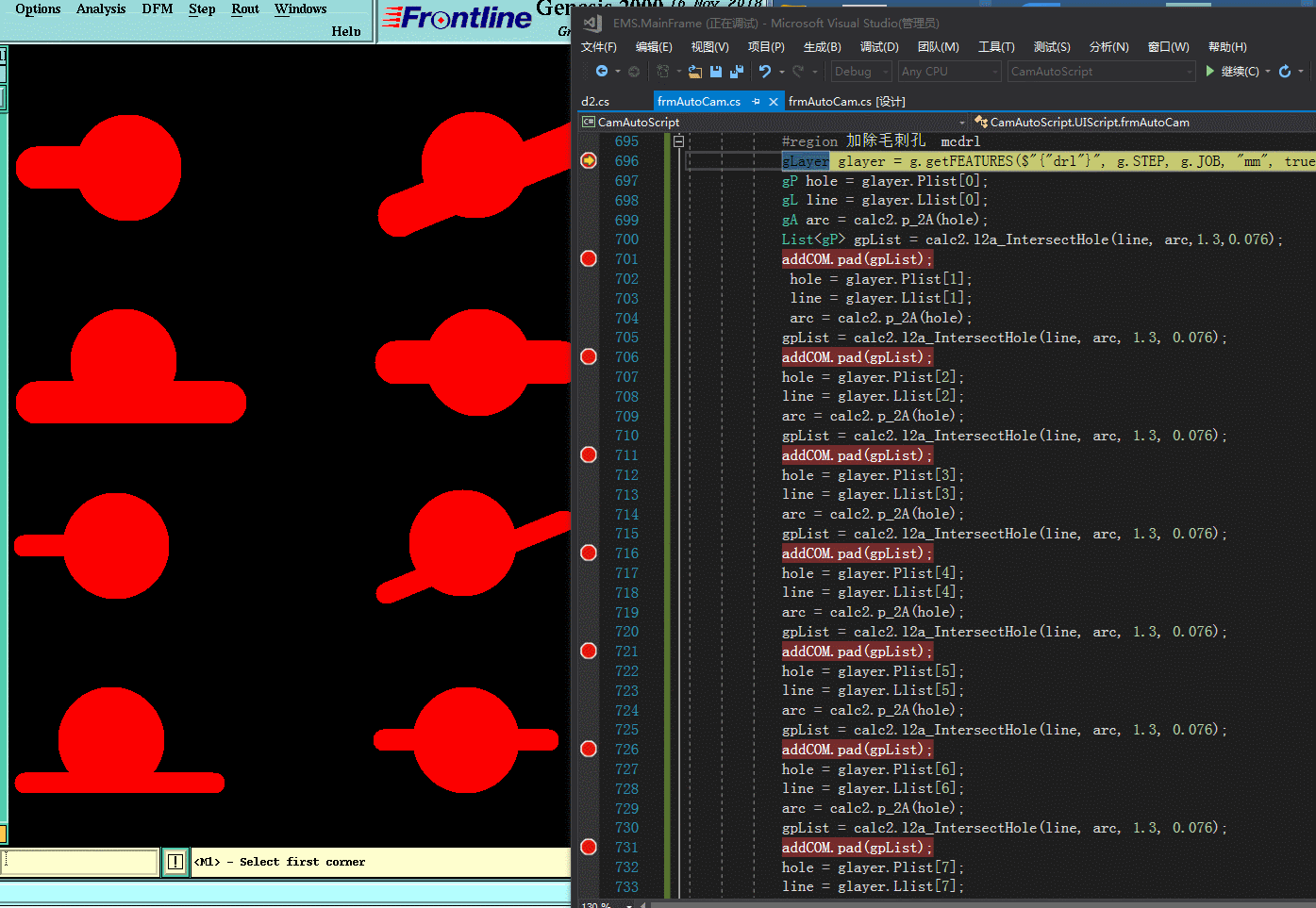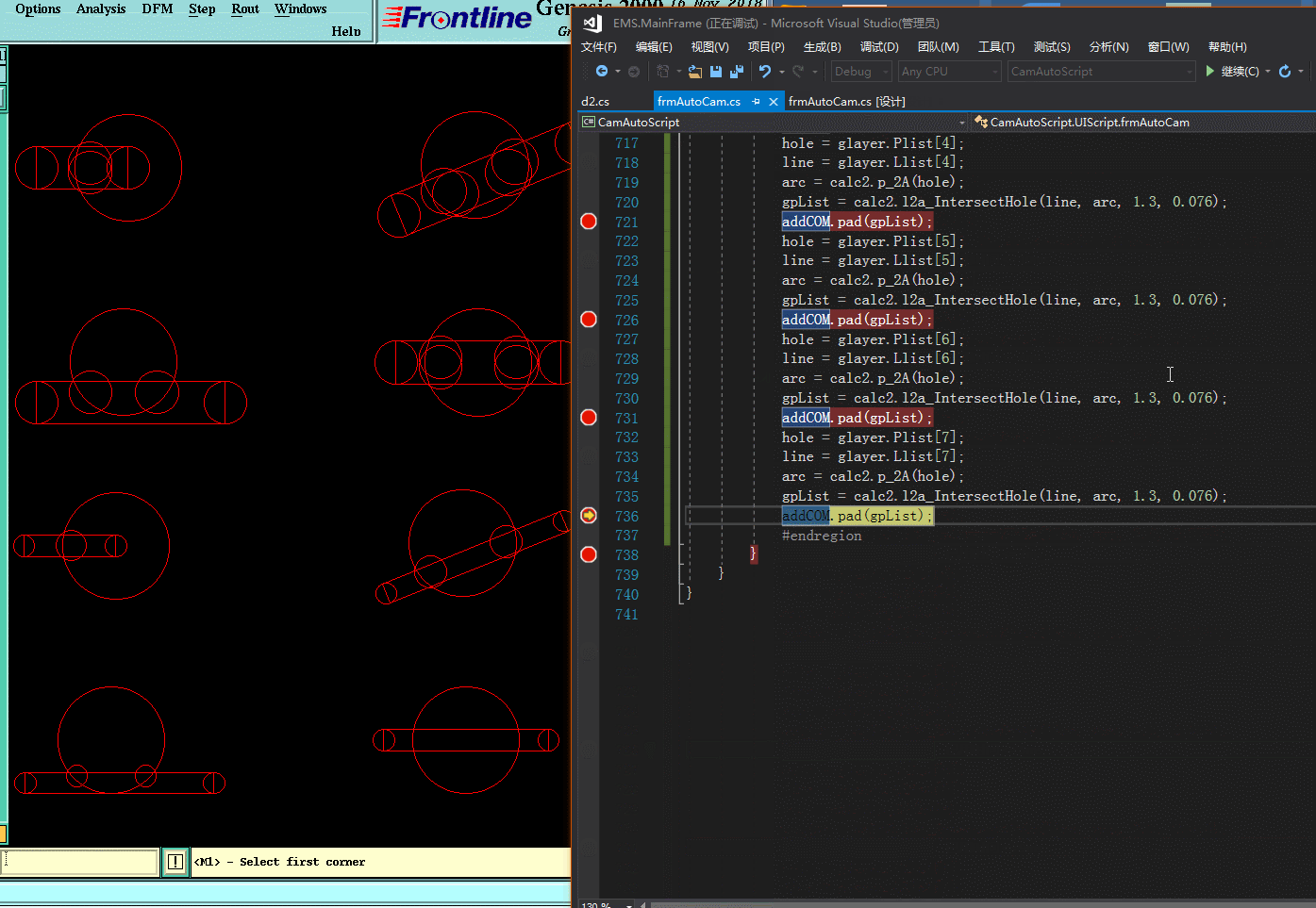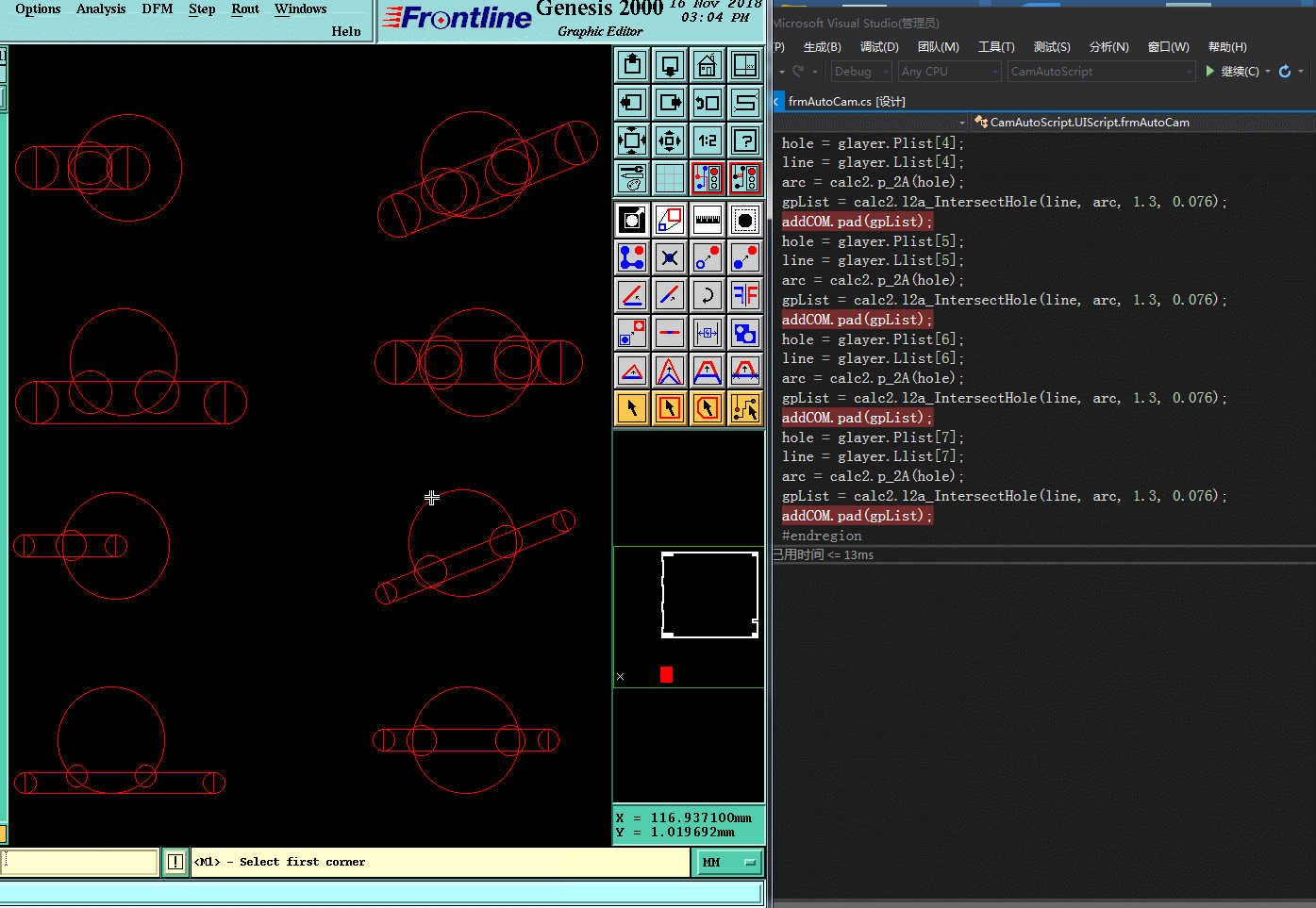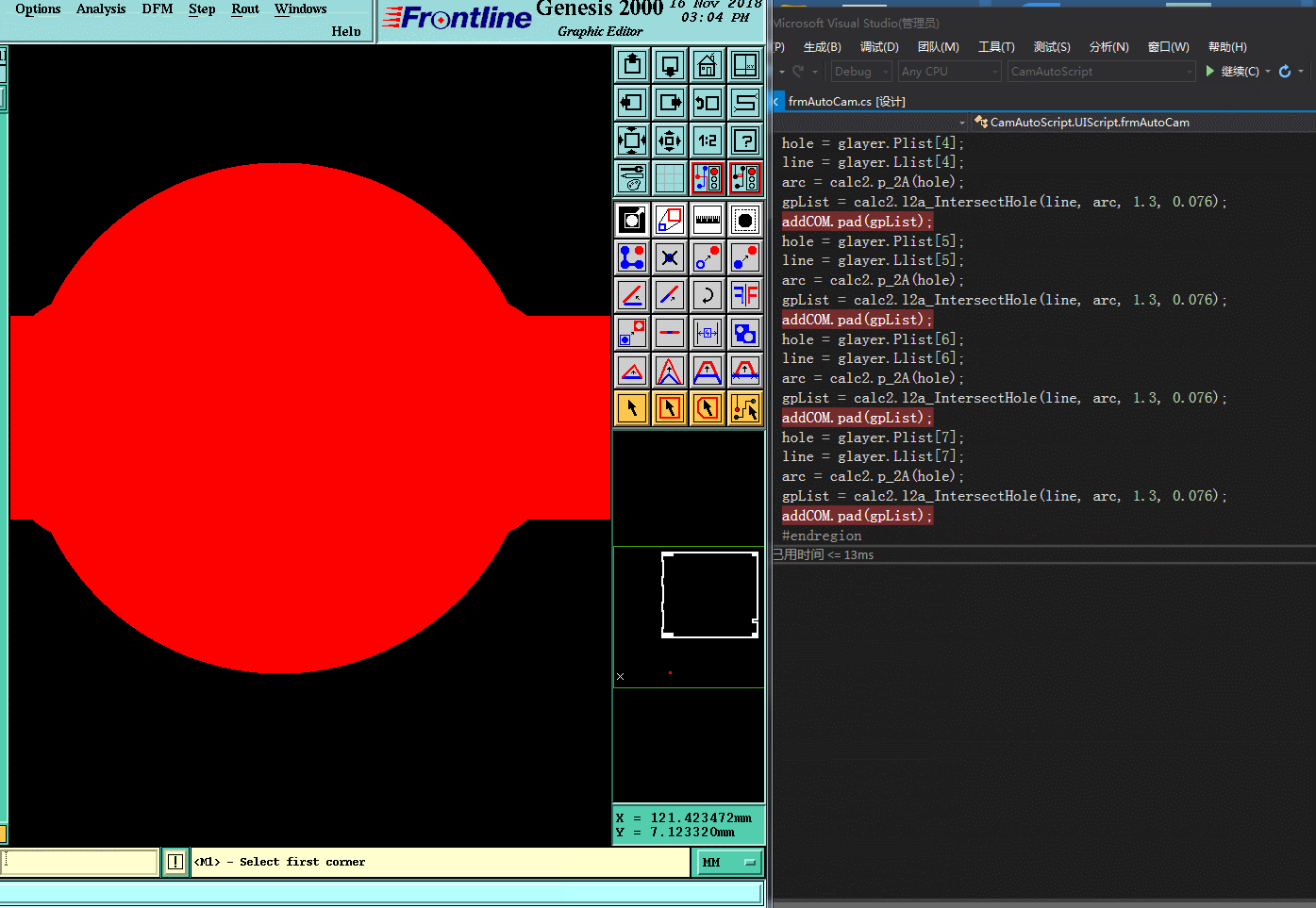
六.實現效果