3.3.2 Arc Consistency Algorithms
提出用於強制執行弧一致性的有效演算法一直被認為是約束推理社群的核心問題。 第一個原因是弧一致性是可能在所有求解器中使用的基本傳播機制。 第二個原因是,允許提高電弧一致性效率的新思想通常可以應用於實現其他區域性一致性的演算法。 這就是為什麼我花了一些時間來介紹已經引入的主要演算法,因為我們知道所涉及的技術可以用於後續章節中提出的其他區域性一致性。 我按照時間順序演示強調了導致當前演算法的增量過程。

AC3
最著名的電弧一致性演算法是Mackworth在[86]中以AC3的名稱提出的演算法。 它被提議用於二進位制規範化網路,並且實際上實現了2個一致性。 在[88]中,它在任意網路中擴充套件到GAC。 這個演算法很容易理解。 一般符號的負擔不是那麼高,我把它呈現在它的一般版本中。 (見演算法3.1。)
GAC3的主要組成部分是弧的修訂,即域的更新和約束。wrt(with respect to)更新域D(xi)與約束c意味著刪除D(xi)中與c不一致的每個值。 函式Revise(xi,c)依次取D(xi)中的每個值vi(第2行),並探索空間πX(c)\ {xi}(D),在c上尋找對vi的支援(行3)。 如果沒有找到這樣的支援,則從D(xi)中移除vi,並且已經改變了D(xi)的事實(第4-5行)。 如果域D(xi)已經減少,則該函式返回true,否則返回false(第6行)。實際上就是更新域,針對一個約束c,在搜尋空間中看是否能找到支援它的值,沒有就從域中刪去這個值。
主演算法是一個簡單的迴圈,它修改弧直到沒有發生變化,以確保所有域都與所有約束一致。為了避免對Revise進行太多無用的呼叫(如AC1或AC2等非常基本的AC演算法中的情況),演算法維護所有對(xi,c)的列表Q,我們不保證D (xi)與c的弧一致。

命題3.27(GAC3)。 GAC3是一種完整的演算法,用於實現在O(er3dr + 1)時間和O(er)空間中執行的弧一致性,其中r是約束中最大的arity。
McGregor提出了一種在AC3中傳播約束的不同方式,後來命名為面向變數,而不是AC3的弧面傳播策略[91]。 在D(xi)(第12行)發生變化後應該修改的所有弧都不是Q,而是放入xi。 Q包含尚未傳播其域中的更改的變數。 當從Q中選擇一個變數xj時,該演算法會修改所有可能因為xj而導致其他缺陷的弧(xi,c)。 這個版本的AC3的實現更簡單,因為Q中的元素只是變數。 但是這種不太精確的資訊有一個缺點。 弧可以修改幾次,而經典的AC3會修改一次。 Boussemart等人提出了McGregor演算法的修改版本,通過為每個弧儲存計數器來解決這個問題[28]。
從現在開始,我轉而使用二進位制規範化網路,因為大多數文獻都使用了這種簡化,我不想假設作者會選擇哪種擴充套件。 然而,這些想法總是允許擴充套件到非規範化的二進位制網路,並且大部分時間都允許擴充套件到具有非二進位制約束的網路。

推論3.28(AC3)。 AC3在O(ed3)時間和O(e)空間中實現二進位制網路的電弧一致性。
AC3的時間複雜度不是最佳的。 函式Revise不記得任何有關其計算結果以支援值的事實導致AC3執行並重做多次相同的約束檢查。
eg 
AC4
AC3不是最優的,Mohr和Henderson提出AC4來改善時間複雜度[92,93]。 與AC3相反,AC4的想法是儲存大量資訊。 AC3在呼叫Revise中執行最少量的工作,只需確保xi的所有剩餘值與c一致並且不記憶任何內容。 如果召回相同的修訂版,要付出的代價是重做大部分工作。 AC4在預處理步驟中儲存最大量的資訊,以避免在刪除傳播期間重複幾次相同的約束檢查。

AC4在演算法3.2中給出。它計算每個三元組(xi,vi,xj)的計數器counter[xi,vi,xj],其中cij∈C和vi∈D(xi)。這個計數器最終會說明vi對cij有多少支援。 AC4還構建列表S [xj,vj],其中包含cij上(xj,vj)支援的所有值。在初始化階段,AC4對所有約束執行所有可能的約束檢查。每次在cij上找到(xi,vi)的支援vj∈D(xj)時,計數器[xi,vi,xj]遞增,並且將(xi,vi)加到S [xj,vj](第3行)和5)。每次在沒有約束支援的情況下找到值時,它將從域中刪除並放入列表Q以供將來傳播(第4行)。初始化完成後,我們進入傳播迴圈(第7行),其中包括傳播Q中值的刪除結果。對於從Q(第8行)中選取的每個值(xj,vj),我們只需要遞減計數器[xi,vi,xj]用於每個值(xi,vi)∈S[xj,vj]以使計數器保持最新(第11行)。如果counter [xi,v i,x j]達到零,這意味著(xj,v j)是cij上(xi,v i)的最後一個支援。 (xi,v i)被移除並放入列表Q(第12和13行)。當Q為空時,我們知道域中剩餘的所有值在其所有約束上都具有非零計數器,因此弧一致。
AC4是後來被稱為“細粒度”演算法[126]的類別中的第一個演算法,因為它們在值的級別上執行傳播(通過列表Q)。 “粗粒度”演算法(例如AC3)在約束(或弧)的水平上傳播,這不太精確並且可能涉及不必要的工作。
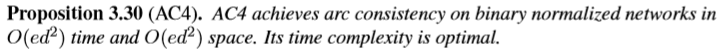
命題3.30(AC4) AC4在O(ed2)時間和O(ed2)空間中實現二進位制歸一化網路的電弧一致性。 它的時間複雜度是最佳的。
We observe that the propagation of the deletion of (y,3) did not require any constraint check. It required traversals of S[..] lists and updates of counters.
雖然在時間上是最佳的,但AC4不僅遭受其高空間複雜性。 其非常昂貴的初始化階段本身可能會過時。 實際上,我們可以非正式地說AC4具有最佳的最壞情況時間複雜度,但它幾乎總是達到這種最壞情況。 華萊士在[120]中討論了這個問題。 此外,即使初始化階段已完成,AC4也會保持一個如此準確的過程檢視,以便花費大量精力更新其計數器並遍歷其列表。 這在例3.31中可見,其中(y,3)的移除引起S [y,3]的遍歷和計數器更新,而所有剩餘值都具有支援。AC4的初始化成本太高了。
由Mohr和Masini在[93]中提出的非二進位制版本GAC4處於3.3.1節中給出的最優O(erdr)時間複雜度,其中r是所有約束中最大的arity。
AC6
Bessiere和Cordier提出了AC6,這是AC3的laziness和AC4的eagerness之間的妥協[15,14]。 AC6背後的動機是保持AC4的最佳最壞情況時間複雜度,並且一旦找到第一個支援就停止搜尋對約束值的支援,如在AC3的修訂中所做的那樣。 此外,AC6保持比AC4更輕的資料結構。 實際上,AC6中的想法不是計算值對約束的所有支援,而只是為了確保它至少有一個。

AC6僅需要列表S,其中S [xj,vj]包含(xj,vj)是當前支援的所有值。 也就是說,(xi,vi)∈S[xj,vj]當且僅當vj是cij上vi的第一個支援。
與AC4一樣,AC6是一種細粒度演算法,因為它沿著值傳播。 當移除的值(xj,v j)沒有機會在D(xi)中引發另一個移除時,即當D(xi)∩S[xj,v j] =∅時,它不會重新考慮約束cij。
![]()
AC2001
在諸如AC4或AC6的細粒度演算法中,傳播是以變數的值為導向的。 刪除值(xj,vj)直接通過Q傳播到值(xi,vi),該值具有(xj,vj)作為支援(即,在S [xj,vi]上的值(xi,vi)])。粗粒度演算法是面向弧的演算法。 它們不會將值清除的後果傳播到其他變數值。雖然粗粒度演算法的傳播方式不太精確,但它們具有雙重優勢。 首先,約束求解器的體系結構(參見3.8節)通常支援面向弧的傳播,而不是面向值的傳播。 其次,所有細粒度演算法都需要支援值的列表S [..]作為資料結構,實現和維護起來更復雜。 這些是AC2001的動機,AC2001是第一個(也是唯一的)最優粗粒度演算法[24,126,25]。
AC2001遵循與AC3相同的框架,但通過在每個約束上儲存每個值的最小支援(如AC6)來實現最優化。 但是,此資訊的儲存和使用方式與AC6中的方式不同。 AC2001不使用列表S [xj,v j]來儲存具有vj作為cij上最小支援的(xi,v i)。 它使用包含vj的指標Last [xi,vi,xj]。
AC2001與AC3的不同之處僅在於其修訂功能和初始化階段,需要將指標Last [xi,v i,x j]初始化為小於minD(xj)的某個虛擬值。 在Revise2001(演算法3.4)中,當發現D(xj)中的值vj支援cij上的(xi,v i)時,AC2001將vj分配給Last [xi,v i,x j](第4行)。 下一次(xi,cij)將被修改,僅當Last [xi,v i,x j]不再在D(xj)(第2行)時,才會尋求(xi,v i)的支援。 更重要的是,獲得最優性是因為D(xj)中小於Last [xi,v i,x j]的值不再被檢查,因為它們在先前對Revise2001的呼叫中已經未成功檢查(第3行)。
![]()
3.3.3 Other Improvements
我已經介紹了在網路上實施弧一致性的主要技術。 存在其他型別的技術以降低電弧一致性的成本。 它們通常被新增到上面提出的一種弧一致性演算法中以改善其效能。 我不能詳盡無遺,但這裡有兩種技術。
Bidirectionality雙向
約束被認為是多向的,因為當發現元組τ在約束c上支援(xi,vi)時,它也支援同一約束上的任何(xj,vj)∈τ。多方向的二進位制版本是 稱為雙向性。 這個屬性看起來很明顯,並沒有像目前為止提供的演算法那樣多。
事實上,AC3在修改修改xi(xi,c)中的xi(演算法3.1中的第12行)後避免將(xj,c)置於Q中時部分使用它:從D(xi)中刪除的值vi沒有支援 c,因此刪除它不能丟棄對D(xj)中的值的支援。
Gaschnig建議更明確地使用雙向性。 演算法DEE [62]是AC3的擴充套件,它使用'Revise-both'程式按順序處理Revise(xi,cij)和Revise(xj,cij)。 作為第一步,Revise-both執行與Revise(xi,cij)相同的工作,但此外,標記D(xj)中的每個值,該值在D(xi)中支援值。 一旦檢查了xi的所有值,修改 - 都修改cj上的xj,只查詢對D(xj)的未標記值的支援。 在第一階段標記的值保證有支援。 DEE不會將這些標記儲存在從Revise到另一個的呼叫中。 此外,在傳播階段,電弧通常一次僅在一個方向上進行修正,這降低了DEE的增益。
雙向性在AC7中被廣泛使用[18,19],AC6的擴充套件。 由於AC6支援的值列表和其他指標,AC7完全利用了雙向性。 這意味著只有在cji(vj,vi)從未檢查cj(vj,vi)的同時在cji上尋找對(xj,vj)的支援時,才會執行約束檢查cij(vi,vj) 並且不存在vj∈D(xj)使得cji(vj,vi)已經被成功檢查為(xj,vj)的支援。 在IlogSolver [71]中使用非二進位制版本的AC7 [23]來傳播一般約束。 至於GAC4,它以最佳的O(erdr)時間複雜度執行。
Lecoutre等人提出了AC2001的幾個擴充套件,允許將AC7中使用的技術適應粗粒度演算法[81]。 AC3.2是一種在正約束檢查上部分利用雙向性的演算法。 AC3.3充分利用正約束檢查的雙向性。 AC3.2 *和AC3.3 *是AC3.2和AC3.3的擴充套件,它們也利用負約束檢查的雙向性,如AC7。 廣泛的實驗表明,AC3.3是最佳標準的一致性,而AC3.2在搜尋過程中保持最佳。
Ordering the propagation list
另一種改善強制弧一致性所需時間的方法是首先修改將修剪最多或最便宜修改的弧。 在他們關於這個主題的開創性論文中,Wallace和Freuder提出了幾種啟發式方法來重新排列AC3中的傳播列表[121]。 在他們分析的不同啟發式方法中,最好的似乎是首先選擇弧(xi,cij),使得要修改的變數xj具有最小的域。
Gent等人將弧度一致性應用於[65]中定義的“約束性”的一般標準。 他們建議首先選擇最小化電弧一致性約束κac的電弧[64]。 他們表明,這種啟發式方法是減少約束檢查次數的好方法,但計算量很大。 有趣的是,他們的標準的近似值給出了Wallace和Freuder提出的一些良好的啟發式演算法。
最近由Boussemart等人提出了關於粗粒度弧一致性演算法的排序啟發式的最全面的研究。在[28]。他們不僅研究了啟發式方法來重新排序傳播列表Q,還研究了我們放入其中的資訊型別。 Q可以是要修改的弧列表,如在常規AC3(弧定向修訂版)中,其域已經被修改為McGregor版本(面向變數的版本)的變數列表,或者具有變數的約束列表他們的計劃修改。變數列表比弧列表短得多,他們表明,當結合面向變數的實現時,啟發式處理Q的時間較少。由於McGregor的演算法遭受冗餘修訂(參見第3.3.2小節),Boussemart等人提出了一個修改版本,它避免了這些冗餘修訂,同時保留了面向變數修訂的優勢。至於儲存約束檢查,他們發現幾個與Wallace和Freuder或van Dongen [121,113]已經提出的啟發式相近的啟發式演算法表現出良好的效能。其中,他們建議採用面向變數的粗粒度演算法實現(他們用AC3.2進行實驗),其中具有最小域的變數首先從Q中選取。
