樹鏈剖分

【11月27日星期二晴】

先【下認識數鏈剖分的概念】

從大佬處摘錄而來，先認識下概念。

樹鏈剖分就是對一棵樹分成幾條鏈，把樹形變為線性，減少處理難度
需要處理的問題：

• 將樹從X到ý結點最短路徑上所有節點的值都加上ž
• 求樹從X到ý結點最短路徑上所有節點的值之和
• 將以X為根節點的子樹內所有節點值都加上ž
• 求以X為根節點的子樹內所有節點值之和

概念

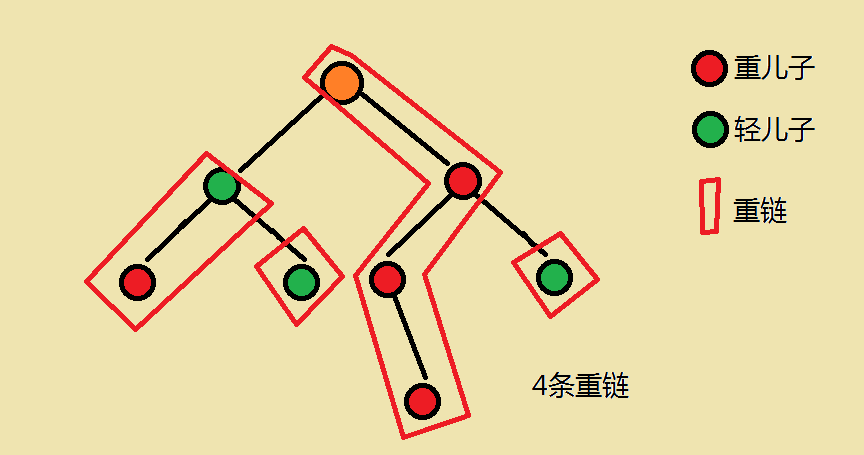
• 重兒子：對於每一個非葉子節點，它的兒子中以那個兒子為根的子樹節點數最大的兒子為該節點的重兒子
• 輕兒子：對於每一個非葉子節點，它的兒子中非重兒子的剩下所有兒子即為輕兒子
• 葉子節點沒有重兒子也沒有輕兒子（因為它沒有兒子..）
• 重邊：一個父親連線他的重兒子的邊稱為重邊（由於考慮到父節點的情況所以不能看作任意兩重兒子的連結邊）
• 輕邊：剩下的即為輕邊
• 重鏈：相鄰重邊連起來的連線一條重兒子的鏈叫重鏈
  • 對於葉子節點，若其為輕兒子，則有一條以自己為起點的長度為1的鏈
  • 每一條重鏈以輕兒子為起點

DFS1（）

這個DFS要處理幾件事情：

• 標記每個點的深度DEP []
• 標記每個點的父親FA []
• 標記每個非葉子節點的子樹大小（含它自己）
• 標記每個非葉子節點的重兒子編號兒子[]

inline void dfs1(int x,int f,int deep){//x當前節點，f父親，deep深度 
    dep[x]=deep;//標記每個點的深度 
    fa[x]=f;//標記每個點的父親 
    siz[x]=1;//標記每個非葉子節點的子樹大小 
    int maxson=-1;//記錄重兒子的兒子數 
    for(Rint i=beg[x];i;i=nex[i]){
        int y=to[i];
        if(y==f)continue;//若為父親則continue 
        dfs1(y,x,deep+1);//dfs其兒子 
        siz[x]+=siz[y];//把它的兒子數加到它身上 
        if(siz[y]>maxson)son[x]=y,maxson=siz[y];//標記每個非葉子節點的重兒子編號 
    }
}//變數解釋見最下面
 

DFS2（）

這個DFS2也要預處理幾件事情

• 標記每個點的新編號
• 賦值每個點的初始值到新編號上
• 處理每個點所在鏈的頂端
• 處理每條鏈

順序：先處理重兒子再處理輕兒子，理由後面說

inline void dfs2(int x,int topf){//x當前節點，topf當前鏈的最頂端的節點 
    id[x]=++cnt;//標記每個點的新編號 
    wt[cnt]=w[x];//把每個點的初始值賦到新編號上來 
    top[x]=topf;//這個點所在鏈的頂端 
    if(!son[x])return;//如果沒有兒子則返回 
    dfs2(son[x],topf);//按先處理重兒子，再處理輕兒子的順序遞迴處理 
    for(Rint i=beg[x];i;i=nex[i]){
        int y=to[i];
        if(y==fa[x]||y==son[x])continue;
        dfs2(y,y);//對於每一個輕兒子都有一條從它自己開始的鏈 
    }
}//變數解釋見最下面

處理問題

注意重要的來了!!!
前面說到dfs2的順序是先處理重兒子再處理輕兒子
我們來模擬一下：

• 因為順序是先重再輕，所以每一條重鏈的新編號是連續的
• 因為是DFS，所以每一個子樹的新編號也是連續的

現在回顧一下我們要處理的問題

• 處理任意兩點間路徑上的點權和
• 處理一點及其子樹的點權和
• 修改任意兩點間路徑上的點權
• 修改一點及其子樹的點權

如圖1所示，當我們要處理任意兩點間路徑時：
設所在鏈頂端的深度更深的那個點為X點

• ans加上x點到x所在鏈頂端這一段區間的點權和
• 把X跳到X所在鏈頂端的那個點的上面一個點

不停執行這兩個步驟，直到兩個點處於一條鏈上，這時再加上此時兩個點的區間和即可

這時我們注意到，我們所要處理的所有區間均為連續編號（新編號），於是想到線段樹，線段用樹處理連續編號區間狀語從句：
每次查詢時間複雜度為O（log2n）O（log2⁡n ）

inline int qRange(int x,int y){
    int ans=0;
    while(top[x]!=top[y]){//當兩個點不在同一條鏈上 
        if(dep[top[x]]<dep[top[y]])swap(x,y);//把x點改為所在鏈頂端的深度更深的那個點
        res=0;
        query(1,1,n,id[top[x]],id[x]);//ans加上x點到x所在鏈頂端 這一段區間的點權和
        ans+=res;
        ans%=mod;//按題意取模 
        x=fa[top[x]];//把x跳到x所在鏈頂端的那個點的上面一個點
    }
    //直到兩個點處於一條鏈上
    if(dep[x]>dep[y])swap(x,y);//把x點深度更深的那個點
    res=0;
    query(1,1,n,id[x],id[y]);//這時再加上此時兩個點的區間和即可
    ans+=res;
    return ans%mod;
}//變數解釋見最下面

2，處理一點及其子樹的點權和：
想到記錄了每個非葉子節點的子樹大小（含它自己），每個並且子樹的新編號都是連續的
於是直接線段樹區間查詢即可
時間複雜度為O（logN）的O（log⁡n）

inline int qSon(int x){
    res=0;
    query(1,1,n,id[x],id[x]+siz[x]-1);//子樹區間右端點為id[x]+siz[x]-1 
    return res;
}

當然，區間修改就和區間查詢一樣的啦~~

inline void updRange(int x,int y,int k){
    k%=mod;
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]])swap(x,y);
        update(1,1,n,id[top[x]],id[x],k);
        x=fa[top[x]];
    }
    if(dep[x]>dep[y])swap(x,y);
    update(1,1,n,id[x],id[y],k);
}

inline void updSon(int x,int k){
    update(1,1,n,id[x],id[x]+siz[x]-1,k);
}//變數解釋見最下面

建樹

既然前面說到要用線段樹，那麼按題意建樹就可以了。

此後，看了篇數鏈剖分的模板，還是可以的就是SPOJ375的例子：程式碼連結，貼上去的。

【現在是晚上9:40了，學習了一整天，然後把洛谷的P3384給過了】

學習了一整天，也用掉了好幾張草稿紙去模擬樹鏈剖分的執行方式，挺好的，剛找到BUG然後過掉了。

就以洛谷的這道題來講一下吧，（打個廣告：樹鏈剖分習題就要上線啦!!!（11月28日上午10時正式開始，歡迎捧場）），我們要有這麼幾種操作和這麼幾種陣列的相關作用：

• w[]陣列：用以記錄原來所對應的每個點的價值；
• head[]：用以鏈式前向星使用；
• depth[]：記錄每個節點距離根節點的深度，我令根節點從0開始；
• root[]：記錄每個節點的父節點，到時候方便我處理不在同一個重鏈上的查詢區間（跟LCA的逼近法相似）；
• size[]：記錄每個節點，以它為根節點，其子節點個數（包含自己）——用以處理該根節點下的更新與求和之用；
• W_son[]：記錄每個節點的重兒子節點，葉子節點的W_son為0；
• id[]：每個節點在dfs2()過後生成的在樹上的對應位置，此處在同一個鏈上的節點應該是連續的；
• top[]：記錄每個節點的所在重鏈的最頂根節點；
• tree[]和lazy[]：這大家都懂得吧，線段樹嘛。

dfs1():

1. 處理深度；
2. 找父節點；
3. 它下面有多少節點；
4. 誰是它的重兒子；
5. size[]求和。

dfs2():

1. 重邊變成重鏈；
2. 將原來的節點按序拍上樹去，就是賦予連續值，就叫做賦新值吧；
3. 重兒子傳遞重鏈；
4. 輕兒子以它為根，構建新重鏈。

Query_range():

1. 首先處理不在同鏈上的節點，先找出他們的值，使兩查詢數在統一鏈上；
2. 統一鏈了之後，就是從上往下線段樹query()即可。

Query_son():

1. 查以該節點為根的節點總權值和，其實就是x節點之下的包括其本身的所有節點和，不就是x～x+size[x]-1嘛。

上個程式碼給大家看看，學習一天的成果，個人感覺美滋滋：

#include <iostream>
#include <cstdio>
#include <cmath>
#include <string>
#include <cstring>
#include <algorithm>
#include <limits>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <map>
#define lowbit(x) ( x&(-x) )
#define pi 3.141592653589793
#define e 2.718281828459045
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int maxN = 4e5+5;
int N, Q, R, Mod, w[maxN], head[maxN], cnt, depth[maxN], root[maxN], size[maxN], W_son[maxN], id[maxN], num, new_W[maxN], top[maxN], tree[maxN<<2], lazy[maxN<<2];
struct Eddge
{
    int nex, to;
    Eddge(int a=-1, int b=0):nex(a), to(b) {}
}edge[maxN];
void addEddge(int u, int v)
{
    edge[cnt] = Eddge(head[u], v);
    head[u] = cnt++;
}
void dfs1(int u, int fa, int deep)
{
    depth[u] = deep;
    root[u] = fa;
    size[u] = 1;
    int maxSon = -1;
    for(int i=head[u]; i!=-1; i=edge[i].nex)
    {
        int v = edge[i].to;
        if(v == fa) continue;
        dfs1(v, u, deep+1);
        size[u] += size[v];
        if(size[v] > maxSon)
        {
            maxSon = size[v];
            W_son[u] = v;
        }
    }
}
void dfs2(int u, int topf)
{
    id[u] = ++num;
    new_W[num] = w[u];
    top[u] = topf;
    if(!W_son[u]) return;
    dfs2(W_son[u], topf);
    for(int i=head[u]; i!=-1; i=edge[i].nex)
    {
        int v = edge[i].to;
        if(v == W_son[u] || v == root[u]) continue;
        dfs2(v, v);
    }
}
void buildTree(int rt, int l, int r)
{
    lazy[rt] = 0;
    if(l == r)
    {
        tree[rt] = new_W[l];
        return;
    }
    int mid = (l + r)>>1;
    buildTree(rt<<1, l, mid);
    buildTree(rt<<1|1, mid+1, r);
    tree[rt] = ( tree[rt<<1] + tree[rt<<1|1] )%Mod;
}
void pushdown(int rt, int l, int r)
{
    if(lazy[rt])
    {
        int mid = (l + r)>>1;
        lazy[rt<<1] += lazy[rt];    lazy[rt<<1]%=Mod;
        lazy[rt<<1|1] += lazy[rt];  lazy[rt<<1|1]%=Mod;
        tree[rt<<1] += lazy[rt]*(mid - l + 1)%Mod;  tree[rt<<1]%=Mod;
        tree[rt<<1|1] += lazy[rt]*(r - mid)%Mod;    tree[rt<<1|1]%=Mod;
        lazy[rt] = 0;
    }
}
void update(int rt, int l, int r, int ql, int qr, int val)
{
    if(ql<=l && qr>=r)
    {
        lazy[rt] += val;
        tree[rt] = ( tree[rt] + val*(r-l+1) )%Mod;
        return;
    }
    pushdown(rt, l, r);
    int mid = (l + r)>>1;
    if(ql>mid) update(rt<<1|1, mid+1, r, ql, qr, val);
    else if(qr<=mid) update(rt<<1, l, mid, ql, qr, val);
    else
    {
        update(rt<<1|1, mid+1, r, ql, qr, val);
        update(rt<<1, l, mid, ql, qr, val);
    }
    tree[rt] = ( tree[rt<<1] + tree[rt<<1|1] )%Mod;
}
int query(int rt, int l, int r, int ql, int qr)
{
    if(ql<=l && qr>=r) return tree[rt];
    pushdown(rt, l, r);
    int mid = (l + r)>>1;
    if(ql>mid) return query(rt<<1|1, mid+1, r, ql, qr);
    else if(qr<=mid) return query(rt<<1, l, mid, ql, qr);
    else
    {
        int ans = query(rt<<1|1, mid+1, r, ql, qr);
        ans = (ans + query(rt<<1, l, mid, ql, qr))%Mod;
        return ans;
    }
}
void update_range(int x, int y, int val)
{
    while(top[x] != top[y])
    {
        if(depth[top[x]] < depth[top[y]]) swap(x, y);
        update(1, 1, N, id[top[x]], id[x], val);
        x = root[top[x]];
    }
    if(depth[x] > depth[y]) swap(x, y);
    update(1, 1, N, id[x], id[y], val);
}
int Query_range(int x, int y)
{
    int ans = 0;
    while(top[x] != top[y])
    {
        if(depth[top[x]] < depth[top[y]]) swap(x, y);
        ans = (ans + query(1, 1, N, id[top[x]], id[x]))%Mod;
        x = root[top[x]];
    }
    if(depth[x] > depth[y]) swap(x, y);
    ans = (ans + query(1, 1, N, id[x], id[y]))%Mod;
    return ans;
}
void update_son(int x, int val)
{
    update(1, 1, N, id[x], id[x]+size[x]-1, val);
}
int Query_son(int x)
{
    return query(1, 1, N, id[x], id[x]+size[x]-1);
}
void init()
{
    cnt = num = 0;
    memset(head, -1, sizeof(head));
    memset(W_son, 0, sizeof(W_son));
}
int main()
{
    while(scanf("%d%d%d%d", &N, &Q, &R, &Mod)!=EOF)
    {
        init();
        for(int i=1; i<=N; i++) scanf("%d", &w[i]);
        for(int i=1; i<N; i++)
        {
            int e1, e2;
            scanf("%d%d", &e1, &e2);
            addEddge(e1, e2);
            addEddge(e2, e1);
        }
        dfs1(R, R, 0);
        dfs2(R, R);
        buildTree(1, 1, N);
        while(Q--)
        {
            int op, x, y, z;
            scanf("%d", &op);
            if(op == 1)
            {
                scanf("%d%d%d", &x, &y, &z);
                update_range(x, y, z);
            }
            else if(op == 2)
            {
                scanf("%d%d", &x, &y);
                printf("%d\n", Query_range(x, y));
            }
            else if(op == 3)
            {
                scanf("%d%d", &x, &z);
                update_son(x, z);
            }
            else
            {
                scanf("%d", &x);
                printf("%d\n", Query_son(x));
            }
        }
    }
    return 0;
}

【11月28日 星期三 晴】

今天補題，過掉了牛客上之前小白賽（神仙場）的D題樹上求和——樹鏈剖分，這道題與模板題不一樣了，但其實沒多大差別，就是推一個求子節點平方和的公式X1^2+X2^2+......+Xn^2；有(x+y)^2=X^2+Y^2+2xy，那麼多幾個x、y也是成立的：(X1+X2+X3+......+Xn+Y)=X1^2+X2^2+......+Xn^2+2*(X1+X2+X3+......+Xn)*Y+Y^2。

那麼，上程式碼吧：

#include <iostream>
#include <cstdio>
#include <cmath>
#include <string>
#include <cstring>
#include <algorithm>
#include <limits>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <map>
#define lowbit(x) ( x&(-x) )
#define pi 3.141592653589793
#define e 2.718281828459045
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int mod = 23333;
const int maxN = 100010;
int N, Q, w[maxN], head[maxN], cnt, depth[maxN], root[maxN], size[maxN], W_son[maxN], top[maxN], id[maxN], num;
ll new_W[maxN], sum[maxN<<2], multi[maxN<<2], lazy[maxN<<2];
struct Eddge
{
    int nex, to;
    Eddge(int a=-1, int b=0):nex(a), to(b) {}
}edge[maxN<<1];
void addEddge(int u, int v)
{
    edge[cnt] = Eddge(head[u], v);
    head[u] = cnt++;
}
void dfs1(int u, int fa, int deep)
{
    root[u] = fa;
    depth[u] = deep;
    size[u] = 1;
    int maxSon = -1;
    for(int i=head[u]; i!=-1; i=edge[i].nex)
    {
        int v = edge[i].to;
        if(v == fa) continue;
        dfs1(v, u, deep+1);
        size[u] += size[v];
        if(size[v] > maxSon)
        {
            maxSon = size[v];
            W_son[u] = v;
        }
    }
}
void dfs2(int x, int topf)
{
    top[x] = topf;
    id[x] = ++num;
    new_W[num] = w[x];
    if(!W_son[x]) return;
    dfs2(W_son[x], topf);
    for(int i=head[x]; i!=-1; i=edge[i].nex)
    {
        int v = edge[i].to;
        if(v == W_son[x] || v == root[x]) continue;
        dfs2(v, v);
    }
}
void pushup(int rt)
{
    sum[rt] = ( sum[rt<<1] + sum[rt<<1|1] )%mod;
    multi[rt] = ( multi[rt<<1] + multi[rt<<1|1] )%mod;
}
void buildTree(int rt, int l, int r)
{
    lazy[rt] = 0;
    if(l == r)
    {
        sum[rt] = new_W[l]%mod;
        multi[rt] = sum[rt] * sum[rt] %mod;
        return;
    }
    int mid = (l + r)>>1;
    buildTree(rt<<1, l, mid);
    buildTree(rt<<1|1, mid+1, r);
    pushup(rt);
}
void pushdown(int rt, int l, int r)
{
    if(lazy[rt])
    {
        lazy[rt]%=mod;
        lazy[rt<<1] = ( lazy[rt<<1] + lazy[rt] )%mod;
        lazy[rt<<1|1] = ( lazy[rt<<1|1] + lazy[rt] )%mod;
        int mid = (l + r)>>1;
        multi[rt<<1] = ( multi[rt<<1] + 2*sum[rt<<1]*lazy[rt]%mod + lazy[rt]*lazy[rt]%mod*(mid - l + 1)%mod )%mod;
        multi[rt<<1|1] = ( multi[rt<<1|1] + 2*sum[rt<<1|1]*lazy[rt]%mod + lazy[rt]*lazy[rt]%mod*(r - mid)%mod )%mod;
        sum[rt<<1] = ( sum[rt<<1] + (mid - l + 1)*lazy[rt] )%mod;
        sum[rt<<1|1] = ( sum[rt<<1|1] + (r - mid)*lazy[rt] )%mod;
        lazy[rt] = 0;
    }
}
void update(int rt, int l, int r, int ql, int qr, ll val)
{
    if(ql<=l && qr>=r)
    {
        lazy[rt] = ( lazy[rt] + val )%mod;
        multi[rt] = ( multi[rt] + 2*sum[rt]*val%mod + val*val%mod*(r - l + 1)%mod );
        sum[rt] = ( sum[rt] + val*(r - l + 1)%mod )%mod;
        return;
    }
    pushdown(rt, l, r);
    int mid = (l + r)>>1;
    if(ql>mid) update(rt<<1|1, mid+1, r, ql, qr, val);
    else if(qr<=mid) update(rt<<1, l, mid, ql, qr, val);
    else
    {
        update(rt<<1, l, mid, ql, qr, val);
        update(rt<<1|1, mid+1, r, ql, qr, val);
    }
    pushup(rt);
}
ll query(int rt, int l, int r, int ql, int qr)
{
    if(ql<=l && qr>=r) return multi[rt]%mod;
    pushdown(rt, l, r);
    int mid = (l + r)>>1;
    if(ql>mid) return query(rt<<1|1, mid+1, r, ql, qr);
    else if(qr<=mid) return query(rt<<1, l, mid, ql, qr);
    else
    {
        ll ans = query(rt<<1, l, mid, ql, mid);
        ans = ( ans + query(rt<<1|1, mid+1, r, mid+1, qr) )%mod;
        return ans;
    }
}
void update_Son(int x, ll val)
{
    val%=mod;
    update(1, 1, N, id[x], id[x]+size[x]-1, val);
}
ll query_Son(int x)
{
    return query(1, 1, N, id[x], id[x]+size[x]-1);
}
void init()
{
    memset(head, -1, sizeof(head));
    cnt = num = 0;
    memset(W_son, 0, sizeof(W_son));
}
int main()
{
    while(scanf("%d%d", &N, &Q)!=EOF)
    {
        init();
        for(int i=1; i<=N; i++) scanf("%d", &w[i]);
        for(int i=1; i<N; i++)
        {
            int e1, e2;
            scanf("%d%d", &e1, &e2);
            addEddge(e1, e2);
            addEddge(e2, e1);
        }
        dfs1(1, 1, 0);
        dfs2(1, 1);
        buildTree(1, 1, N);
        while(Q--)
        {
            int op, x, y;
            scanf("%d", &op);
            if(op == 1)
            {
                scanf("%d%d", &x, &y);
                update_Son(x, y);
            }
            else
            {
                scanf("%d", &x);
                printf("%lld\n", query_Son(x));
            }
        }
    }
    return 0;
}

感覺還不錯哦，對於DFS1()以及DFS2()有了更深的瞭解，多做題吧，還有一套，歡迎各大牛前來AK。