樹鏈剖分的學習記錄
先來回顧兩個問題: 1,將樹從x到y結點最短路徑上所有節點的值都加上z
這也是個模板題了吧
我們很容易想到,樹上差分可以以O(n+m)的優秀複雜度解決這個問題
2,求樹從x到y結點最短路徑上所有節點的值之和
lca大水題,我們又很容易地想到,dfs O(n)預處理每個節點的dis(即到根節點的最短路徑長度)
然後對於每個詢問,求出x,y兩點的lca,利用lca的性質distance ( x , y ) = dis ( x ) + dis ( y ) - 2 * dis ( lca )求出結果
時間複雜度O(mlogn+n)
現在來思考一個bug: 如果剛才的兩個問題結合起來,成為一道題的兩種操作呢?
剛才的方法顯然就不夠優秀了(每次詢問之前要跑dfs更新dis)
樹鏈剖分華麗登場 樹剖是通過輕重邊剖分將樹分割成多條鏈,然後利用資料結構來維護這些鏈(本質上是一種優化暴力)
首先明確概念:
重兒子:父親節點的所有兒子中子樹結點數目最多(size最大)的結點;
輕兒子:父親節點中除了重兒子以外的兒子;
重邊:父親結點和重兒子連成的邊;
輕邊:父親節點和輕兒子連成的邊;
重鏈:由多條重邊連線而成的路徑;
輕鏈:由多條輕邊連線而成的路徑;
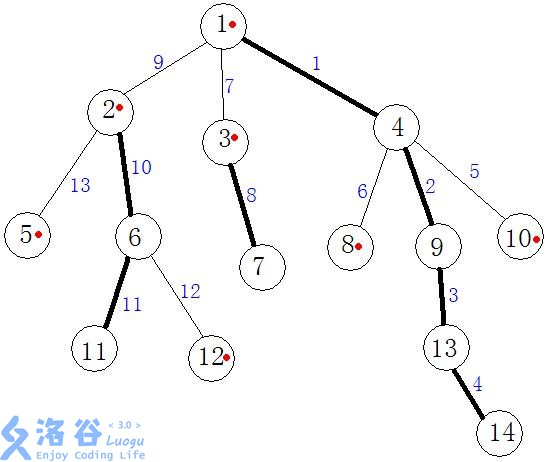
比如上面這幅圖中,用黑線連線的結點都是重結點,其餘均是輕結點,
2-11就是重鏈,2-5就是輕鏈,用紅點標記的就是該結點所在重鏈的起點,也就是下文提到的top結點,
還有每條邊的值其實是進行dfs時的執行序號。
變數宣告:
const int maxn=1e5+10;
struct edge{
int next,to;
}e[2*maxn];
struct Node{
int sum,lazy,l,r,ls,rs;
}node[2*maxn];
int rt,n,m,r,a[maxn],cnt,head[maxn],f[maxn],d[maxn],size[maxn],son[maxn],rk[maxn],top[maxn],id[maxn];| 名稱 | 解釋 |
| f[u] | 儲存結點u的父親節點 |
| d[u] | 儲存結點u的深度值 |
| size[u] | 儲存以u為根的子樹節點個數 |
| son[u] | 儲存重兒子 |
| rk[u] | 儲存當前dfs標號在樹中所對應的節點 |
| top[u] | 儲存當前節點所在鏈的頂端節點 |
| id[u] | 儲存樹中每個節點剖分以後的新編號(DFS的執行順序) |
我們要做的就是(樹鏈剖分的實現):
1,對於一個點我們首先求出它所在的子樹大小,找到它的重兒子(即處理出size,son陣列), 解釋:比如說點1,它有三個兒子2,3,4
2所在子樹的大小是5
3所在子樹的大小是2
4所在子樹的大小是6
那麼1的重兒子是4
ps:如果一個點的多個兒子所在子樹大小相等且最大
那隨便找一個當做它的重兒子就好了
葉節點沒有重兒子,非葉節點有且只有一個重兒子
2,在dfs過程中順便記錄其父親以及深度(即處理出f,d陣列),操作1,2可以通過一遍dfs完成
void dfs1(int u,int fa,int depth) //當前節點、父節點、層次深度
{
f[u]=fa;
d[u]=depth;
size[u]=1; //這個點本身size=1
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if(v==fa)
continue;
dfs1(v,u,depth+1); //層次深度+1
size[u]+=size[v]; //子節點的size已被處理,用它來更新父節點的size
if(size[v]>size[son[u]])
son[u]=v; //選取size最大的作為重兒子
}
}
//進入
dfs1(root,0,1);
dfs跑完大概是這樣的,大家可以手動模擬一下
3,第二遍dfs,然後連線重鏈,同時標記每一個節點的dfs序,並且為了用資料結構來維護重鏈,我們在dfs時保證一條重鏈上各個節點dfs序連續(即處理出陣列top,id,rk)
void dfs2(int u,int t) //當前節點、重鏈頂端
{
top[u]=t;
id[u]=++cnt; //標記dfs序
rk[cnt]=u; //序號cnt對應節點u
if(!son[u])
return;
dfs2(son[u],t);
/*我們選擇優先進入重兒子來保證一條重鏈上各個節點dfs序連續,
一個點和它的重兒子處於同一條重鏈,所以重兒子所在重鏈的頂端還是t*/
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if(v!=son[u]&&v!=f[u])
dfs2(v,v); //一個點位於輕鏈底端,那麼它的top必然是它本身
}
}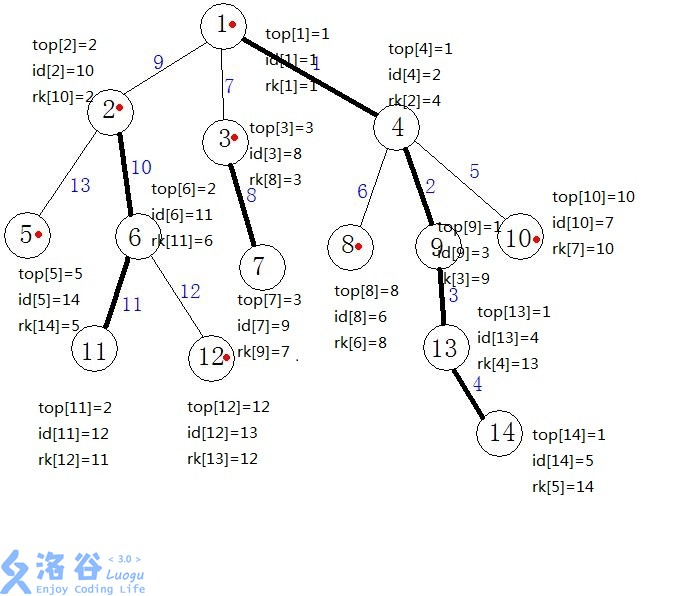
dfs跑完大概是這樣的,大家可以手動模擬一下
4,兩遍dfs就是樹鏈剖分的主要處理,通過dfs我們已經保證一條重鏈上各個節點dfs序連續,那麼可以想到,我們可以通過資料結構(以線段樹為例)來維護一條重鏈的資訊 回顧上文的那個題目,修改和查詢操作原理是類似的,以查詢操作為例,其實就是個LCA,不過這裡使用了top來進行加速,因為top可以直接跳轉到該重鏈的起始結點,輕鏈沒有起始結點之說,他們的top就是自己。需要注意的是,每次迴圈只能跳一次,並且讓結點深的那個來跳到top的位置,避免兩個一起跳從而插肩而過。
int sum(int x,int y)
{
int ans=0,fx=top[x],fy=top[y];
while(fx!=fy) //兩點不在同一條重鏈
{
if(d[fx]>=d[fy])
{
ans+=query(id[fx],id[x],rt); //線段樹區間求和,處理這條重鏈的貢獻
x=f[fx],fx=top[x]; //將x設定成原鏈頭的父親結點,走輕邊,繼續迴圈
}
else
{
ans+=query(id[fy],id[y],rt);
y=f[fy],fy=top[y];
}
}
//迴圈結束,兩點位於同一重鏈上,但兩點不一定為同一點,所以我們還要統計這兩點之間的貢獻
if(id[x]<=id[y])
ans+=query(id[x],id[y],rt);
else
ans+=query(id[y],id[x],rt);
return ans;
}大家如果明白了樹鏈剖分,也應該有舉一反三的能力(反正我沒有),修改和LCA就留給大家自己完成了
5,樹鏈剖分的時間複雜度 樹鏈剖分的兩個性質:
1,如果(u, v)是一條輕邊,那麼size(v) < size(u)/2;
2,從根結點到任意結點的路所經過的輕重鏈的個數必定都小於logn;
可以證明,樹鏈剖分的時間複雜度為O(nlog^2n)
#include<iostream>
#include<cstdio>
using namespace std;
const int maxn=1e5+10;
struct edge{
int next,to;
}e[2*maxn];
struct Node{
int sum,lazy,l,r,ls,rs;
}node[2*maxn];
int rt,n,m,r,a[maxn],cnt,head[maxn],f[maxn],d[maxn],size[maxn],son[maxn],rk[maxn],top[maxn],tid[maxn];
void add_edge(int x,int y)
{
e[++cnt].next=head[x];
e[cnt].to=y;
head[x]=cnt;
}
void dfs1(int u,int fa,int depth)
{
f[u]=fa;
d[u]=depth;
size[u]=1;
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if(v==fa)
continue;
dfs1(v,u,depth+1);
size[u]+=size[v];
if(size[v]>size[son[u]])
son[u]=v;
}
}
void dfs2(int u,int t)
{
top[u]=t;
tid[u]=++cnt;
rk[cnt]=u;
if(!son[u])
return;
dfs2(son[u],t);
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if(v!=son[u]&&v!=f[u])
dfs2(v,v);
}
}
void pushup(int x)
{
node[x].sum=(node[node[x].ls].sum+node[node[x].rs].sum+node[x].lazy*(node[x].r-node[x].l+1));
}
void build(int li,int ri,int cur)
{
if(li==ri)
{
node[cur].ls=node[cur].rs=-1;
node[cur].l=node[cur].r=li;
node[cur].sum=a[rk[li]];
return;
}
int mid=(li+ri)>>1;
node[cur].ls=cnt++;
node[cur].rs=cnt++;
build(li,mid,node[cur].ls);
build(mid+1,ri,node[cur].rs);
node[cur].l=node[node[cur].ls].l;
node[cur].r=node[node[cur].rs].r;
pushup(cur);
}
void update(int li,int ri,int c,int cur)
{
if(li<=node[cur].l&&node[cur].r<=ri)
{
node[cur].sum+=c*(node[cur].r-node[cur].l+1);
node[cur].lazy+=c;
return;
}
int mid=(node[cur].l+node[cur].r)>>1;
if(li<=mid)
update(li,ri,c,node[cur].ls);
if(mid<ri)
update(li,ri,c,node[cur].rs);
pushup(cur);
}
int query(int li,int ri,int cur)
{
if(li<=node[cur].l&&node[cur].r<=ri)
return node[cur].sum;
int tot=node[cur].lazy*(min(node[cur].r,ri)-max(node[cur].l,li)+1);
int mid=(node[cur].l+node[cur].r)>>1;
if(li<=mid)
tot+=query(li,ri,node[cur].ls);
if(mid<ri)
tot+=query(li,ri,node[cur].rs);
return tot;
}
int sum(int x,int y)
{
int ans=0,fx=top[x],fy=top[y];
while(fx!=fy)
{
if(d[fx]>=d[fy])
{
ans+=query(tid[fx],tid[x],rt);
x=f[fx];
}
else
{
ans+=query(tid[fy],tid[y],rt);
y=f[fy];
}
fx=top[x];
fy=top[y];
}
if(tid[x]<=tid[y])
ans+=query(tid[x],tid[y],rt);
else
ans+=query(tid[y],tid[x],rt);
return ans;
}
void updates(int x,int y,int c)
{
int fx=top[x],fy=top[y];
while(fx!=fy)
{
if(d[fx]>=d[fy])
{
update(tid[fx],tid[x],c,rt);
x=f[fx];
}
else
{
update(tid[fy],tid[y],c,rt);
y=f[fy];
}
fx=top[x];
fy=top[y];
}
if(tid[x]<=tid[y])
update(tid[x],tid[y],c,rt);
else
update(tid[y],tid[x],c,rt);
}
int main()
{
cin>>n>>m>>r;
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=1;i<n;i++)
{
int x,y;
cin>>x>>y;
add_edge(x,y);
add_edge(y,x);
}
cnt=0;
dfs1(r,0,1);
dfs2(r,r);
cnt=0;
rt=cnt++;
build(1,n,rt);
for(int i=1;i<=m;i++)
{
int op,x,y,z;
cin>>op;
if(op==1)
{
cin>>x>>y>>z;
updates(x,y,z);
}
else if(op==2)
{
cin>>x>>y;
cout<<sum(x,y)<<endl;
}
else if(op==3)
{
cin>>x>>z;
//子樹也有連續區間的性質
update(tid[x],tid[x]+size[x]-1,z,rt);
}
else if(op==4)
{
cin>>x;
cout<<query(tid[x],tid[x]+size[x]-1,rt)<<endl;
}
}
return 0;
}