學習筆記之——Normalization

阿新 • • 發佈：2018-11-30

本博文是關於normalization的介紹博文。

Batch Normalization

Layer normalization

Weight Normalization

Instance normalization

Group normalization

Switchable Normalization

Reference

Normalization. It is well-known that normalizing the input data makes training faster. To normalize hidden features, initialization methods have been derived based on strong assumptions of feature distributions, which can become invalid when training evolves.

對於normalization，目前主要有以下幾個方法

Batch Normalization

論文連結（https://arxiv.org/pdf/1502.03167.pdf）

首先，在進行網路訓練前，一般要對資料做歸一化，使其分佈一致，但是在深度神經網路訓練過程中，通常以送入網路的每一個batch訓練，這樣每個batch具有不同的分佈；此外，為了解決internal covarivate shift問題（這個問題定義是隨著batch normalizaiton這篇論文提出的，在訓練過程中，資料分佈會發生變化，對下一層網路的學習帶來困難）所以batch normalization就是強行將資料拉回到均值為0，方差為1的正太分佈上，這樣不僅資料分佈一致，而且避免發生梯度消失。

那為什麼要進行歸一化呢？由於ANN學習過程的本質就是為了學習資料的分佈，一旦訓練資料於測試資料分佈不同，那麼網路的泛化能力也大大下降；另一方面，一旦每批訓練資料的分佈各不相同（batch size），那麼網路就要在每次迭代都去學習適應不同的分佈，這樣將會大大降低網路的訓練速度。而且在訓練的過程中，經過一層層的網路運算，中間層的學習到的資料分佈也是發生著挺大的變化，這就要求我們必須使用一個很小的學習率和對引數很好的初始化，但是這麼做會讓訓練過程變得慢而且複雜。在論文中，這種現象被稱為Internal Covariate Shift。為了降低Internal Covariate Shift帶來的影響，其實只要進行歸一化就可以的。比如，把network每一層的輸出都整為方差為1，均值為0的正態分佈，這樣看起來是可以解決問題，但network好不容易學習到的資料特徵，一下子又相當於沒有學習了。所以作者就進行：變換重構，引入了兩個可以學習的引數γ、β：

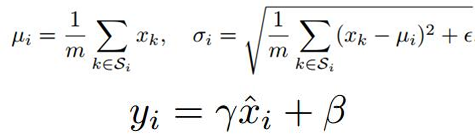
BN帶來的優勢

但是。BN會受到batchsize大小的影響。如果batchsize太小，算出的均值和方差就會不準確，如果太大，視訊記憶體又可能不夠用。

However, the BN has several disadvantages:

It is sensitive to the size of batchsize (it is required for BN to work with a sufficiently large batch size, e.g., 32 per worker). Because the mean and variance of each calculation are on one batch, if the batchsize is too small, the calculated mean and variance are not enough to represent the whole data distribution. so BN’s error increases rapidly when the batch size becomes smaller, caused by inaccurate batch statistics estimation. A small batch leads to inaccurate estimation of the batch statistics, and reducing BN’s batch size increases the model error dramatically (as can be seen from the figure) If the batch size is too small, the calculated mean and variance will be inaccurate. If it is too large, the memory of GPU may not be enough.
When BN is actually used, it is necessary to calculate and save statistical information such as the mean and variance of a certain layer of neural network batch. It is convenient to use BN for a fixed depth forward neural network (DNN, CNN); However, for RNN, the length of the sequence is inconsistent. In other words, the depth of the RNN is not fixed. Different time-steps need to store different statics features. There may be a special sequence that is much longer than other sequences, so when training, The calculation is very troublesome. So there is LN.

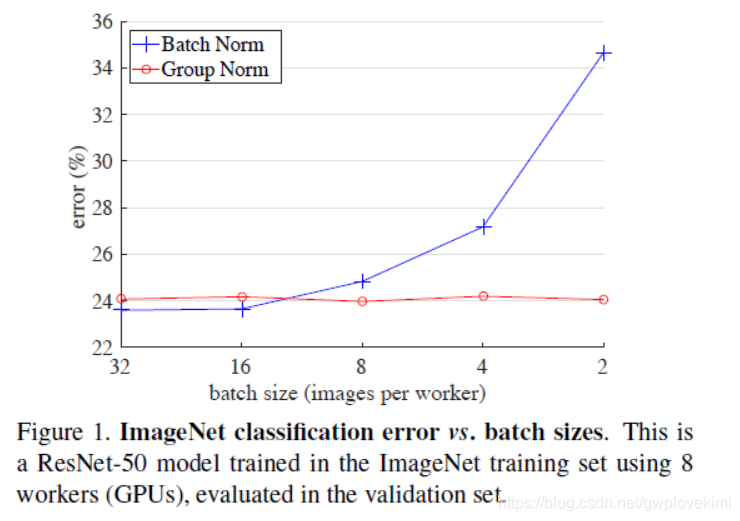
一個較好的介紹材料https://zhuanlan.zhihu.com/p/34480619

首先應該理解什麼是feature scaling。此處用一個簡單的圖示意

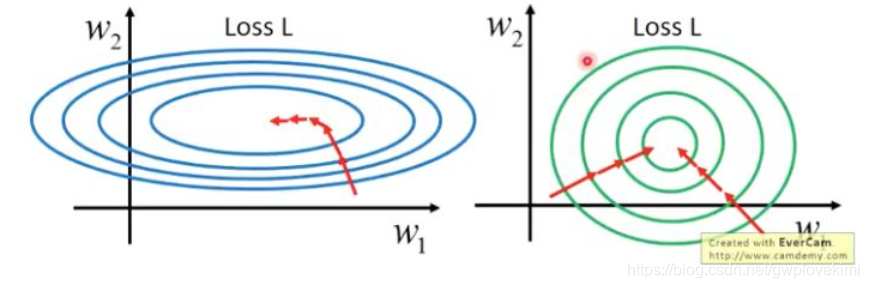
第二個概念Internal Covariate Shift

我們train神經網路的過程，就是對於其中每一層layer中的weights的學習的過程，而通過正向傳播和反向傳播的相互作用，每一層的layer會不斷的變化，這也就導致了其input和output在不斷的變化。但是，當我們固定下來一個方向的數值後，再去調整另外一個方向的數值，使得其與前面的方向匹配，那麼，我們就得到了最終想要的目的。對於不加bn其實也可以解決我們的問題，就是通過非常小的learning_rate來彌補這種雙向變化的空缺，但是訓練的過程將會非常慢

第三個概念batch

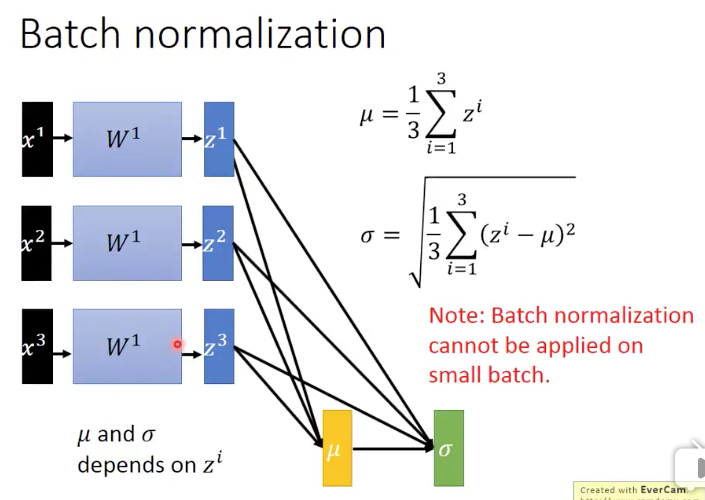
$\mu$ 的值是來自 $z_1,z_2,z_3$ 的， $\delta$ 的值是來自 $\mu$ 和 $z_1,z_2,z_3$ 的。注意：BN是不能夠應用到小資料batch上的，因為我們知道，在計算均值和方差的時候，非常小的batch是沒辦法來衡量整個training set的均值和方差的。而如果我們要去計算整個training set的均值和方差，就會太浪費時間。其實我們真正想要的 $\mu$ 和 $\delta$ 的值就是整個training set上得到的。

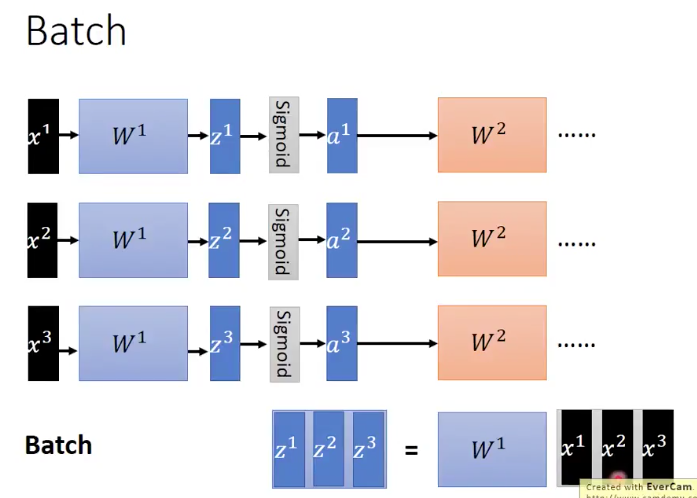
上面這張圖是說，一個batch裡面現在有 $x_1,x_2,x_3$ 這三個資料，然後通過同一組parameters，我們得到了 $z_1,z_2,z_3$ ，然後在經過activation function，得到了 $a_1,a_2,a_3$ ，依次不斷input下去。而當我們把 $x_1,x_2,x_3$ 都同時放進一個matrix裡面的時候，將 $W_1$ 放到這個matrix的前面，我們就能得到兩個matrix的乘法操作，最終得到 $z_1,z_2,z_3$ 。比起分別計算三次矩陣乘法得到 $z_1,z_2,z_3$ 和放到一個矩陣中，平行化計算一次來說。第二種方法明顯加快了運算的速度，這也就是GPU加速batch進行訓練的原理了。

第四個概念，BN是怎麼操作的呢

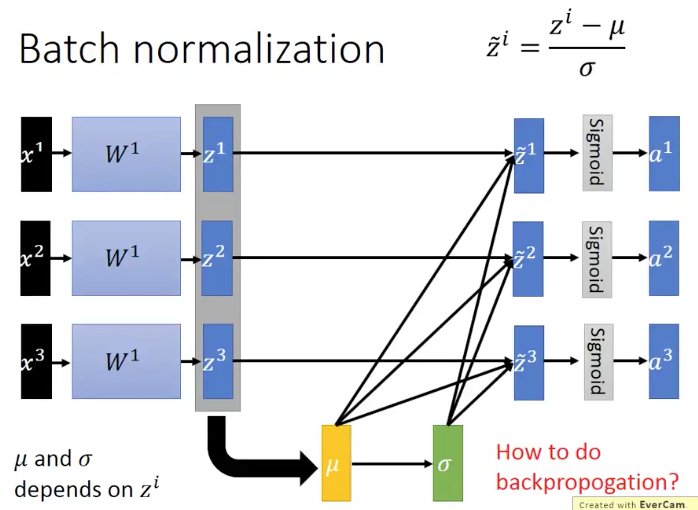
多引入一組獨立的引數 $(\gamma,\beta)$ ，這組parameter和輸入的batch資料無關。是神經網路能夠通過學習自己學到的。而 $(\mu,\delta)$ 卻是和輸入的batch資料有關的。

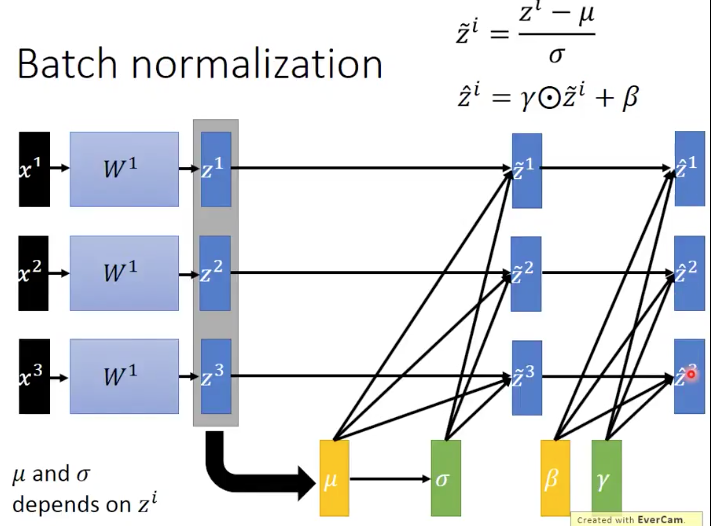
在training階段，NB的表現如下圖所示

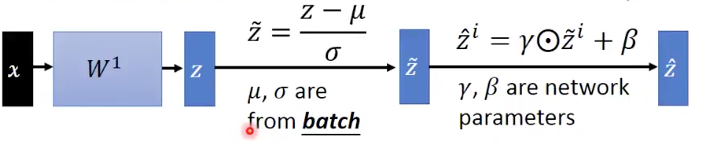
在testing階段，輸入的是一個data，並不是像train那樣，輸入的是一個batch的data，那麼關於引數 $(\mu,\delta)$ 的資訊，我們沒辦法得到。為此可以在我們training的過程中，把每個batch所得到的 $\mu,\delta$ 都儲存下來，然後用平均的 $\mu,\delta$ 來代替我們最終test時候的 $\mu,\delta$

BN的優勢：

能夠減少Interal Covariate Shift的問題，從而減少train的時間，使得對於deep網路的訓練更加可行。
消除梯度消失和梯度爆炸的問題，特別是對sigmoid和tanh函式
對於引數的初始化影響更小即使對於某組parameter同時乘以k倍後，最終的結果還是會keep不變的
能夠減少overfitting問題的發生

Layer normalization

論文連結（https://arxiv.org/pdf/1607.06450v1.pdf）

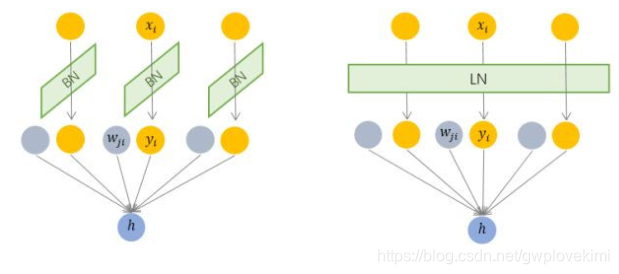
由圖可以看出BN是對input tensor的每個通道進行mini-batch級別的Normalization。而LN則是對所有通道的input tensor進行Normalization（BN僅針對單個神經元，而LN考慮一層的資訊，計算該層輸入的平均值和方差作為規範化標準，對該層的所有輸入施行同一個規範化操作）此外，由於無需儲存mini-batch的均值和方差，節省了儲存空間。然而，對於相似度相差較大的特徵，LN會降低模型的表示能力，此種情形下BN更好（因為BN可對單個神經元訓練得到）

下面給出本人做彙報時的總結ppt

batch normalization存在以下缺點：

對batchsize的大小比較敏感，由於每次計算均值和方差是在一個batch上，所以如果batchsize太小，則計算的均值、方差不足以代表整個資料分佈；
BN實際使用時需要計算並且儲存某一層神經網路batch的均值和方差等統計資訊，對於對一個固定深度的前向神經網路（DNN，CNN）使用BN，很方便；但對於RNN來說，sequence的長度是不一致的，換句話說RNN的深度不是固定的，不同的time-step需要儲存不同的statics特徵，可能存在一個特殊sequence比其他sequence長很多，這樣training時，計算很麻煩。

與BN不同，LN是針對深度網路的某一層的所有神經元的輸入按以下公式進行normalize操作

BN與LN的區別在於：

LN中同層神經元輸入擁有相同的均值和方差，不同的輸入樣本有不同的均值和方差；
BN中則針對不同神經元輸入計算均值和方差，同一個batch中的輸入擁有相同的均值和方差。

所以，LN不依賴於batch的大小和輸入sequence的深度，因此可以用於batchsize為1和RNN中對邊長的輸入sequence的normalize操作。

Weight Normalization

論文（《Weight Normalization: A Simple Reparameterization to Accelerate Training of Deep Neural Networks》）

Instead of operating on features, Weight Normalization (WN) proposes to normalize the filter weights.只是對濾波器的權重做歸一化處理。將權重分為模和方向兩個分量，並分別進行訓練。不依賴於輸入資料的分佈（屬於引數規範化。而前面的LN、BN屬於特徵規範化）

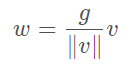
Instance normalization

論文連結（https://arxiv.org/pdf/1607.08022.pdf）

https://github.com/DmitryUlyanov/texture_nets

BN注重對每個batch進行歸一化，保證資料分佈一致，因為判別模型中結果取決於資料整體分佈。但是影象風格轉移中，生成結果主要依賴於某個影象例項，所以對整個batch歸一化不適合影象風格化中，因而對HW做歸一化。可以加速模型收斂，並且保持每個影象例項之間的獨立。

Group normalization

論文連結（https://arxiv.org/pdf/1803.08494.pdf）

主要是針對Batch Normalization對小batchsize效果差，GN將channel方向分group，然後每個group內做歸一化。算的是channel方向每個group的均值和方差，這樣與batchsize無關，不受其約束。

深度網路中的資料維度一般是[N, C, H, W]或者[N, H, W, C]格式，N是batch size，H/W是feature的高/寬，C是feature的channel，壓縮H/W至一個維度

作者發現很多經典的特徵例如 SIFT和 HOG是分組的特徵並涉及分組的歸一化。GN介於LN和IN之間，其首先將channel分為許多組（group），對每一組做歸一化，及先將feature的維度由[N, C, H, W]reshape為[N, G，C//G , H, W]，歸一化的維度為[C//G , H, W]。GN的極端情況就是LN和I N，分別對應G等於C和G等於1

BN、LN、IN、GN的區別：

下面給出參考程式碼

https://github.com/taokong/group_normalization

https://github.com/shaohua0116/Group-Normalization-Tensorflow

Switchable Normalization

論文連結（https://arxiv.org/pdf/1806.10779.pdf）

https://github.com/switchablenorms/Switchable-Normalization

本篇論文作者認為，

第一，歸一化雖然提高模型泛化能力，然而歸一化層的操作是人工設計的。在實際應用中，解決不同的問題原則上需要設計不同的歸一化操作，並沒有一個通用的歸一化方法能夠解決所有應用問題；
第二，一個深度神經網路往往包含幾十個歸一化層，通常這些歸一化層都使用同樣的歸一化操作，因為手工為每一個歸一化層設計操作需要進行大量的實驗。

因此作者提出自適配歸一化方法——Switchable Normalization（SN）來解決上述問題。與強化學習不同，SN使用可微分學習，為一個深度網路中的每一個歸一化層確定合適的歸一化操作。

Reference

https://blog.csdn.net/liuxiao214/article/details/81037416

https://blog.csdn.net/remanented/article/details/79980486

https://blog.csdn.net/antkillerfarm/article/details/83745601

https://mp.weixin.qq.com/s/H2GmqloNumttFlaSArjgUg

https://blog.csdn.net/zziahgf/article/details/83590059

學習筆記之——Normalization

Batch Normalization

Layer normalization

Weight Normalization

Instance normalization

Group normalization

Switchable Normalization

Reference

學習筆記之——Normalization

SAS學習筆記之函數應用

c#學習筆記之Application.DoEvents應用

[C#學習筆記之異步編程模式2]BeginInvoke和EndInvoke方法 (轉載)

.NET學習筆記之ADO.NET

,NET學習筆記之ADO.NET

Metasploit學習筆記之——情報搜集

鋒利的JQuery學習筆記之JQuery

java入門學習筆記之1(類的定義，代碼的編譯執行)

python學習筆記之列表與元組

Scala 學習筆記之函數(1)

Scala 學習筆記之集合(2)

MySQ學習筆記之十 NULL值處理

Scala 學習筆記之集合(7) Option

C++學習筆記之泛型算法

Scala 學習筆記之集合(9) 集合常用操作匯總

vue2.0學習筆記之webpack-simple模板中的路由簡單配置案例

vue2.0學習筆記之自定義組件

PyTorch學習筆記之初識word_embedding

Kafka 學習筆記之架構

學習筆記之——Normalization

Batch Normalization

Layer normalization

Weight Normalization

Instance normalization

Group normalization

Switchable Normalization

Reference

相關推薦