ai">aiai (i.e. di≤aidi≤ai);

the diameter of the graph is maximum possible.

Output the resulting graph or report that no solution exists.

Input

The first line contains a single integer nn (3≤n≤5003≤n≤500) — the number of vertices in the graph.

The second line contains nn integers a1,a2,…,ana1,a2,…,an (1≤ai≤n−11≤ai≤n−1) — the upper limits to vertex degrees.

Output

Print "NO" if no graph can be constructed under the given conditions.

Otherwise print "YES" and the diameter of the resulting graph in the first line.

The second line should contain a single integer mm — the number of edges in the resulting graph.

The ii-th of the next mm lines should contain two integers vi,uivi,ui (1≤vi,ui≤n1≤vi,ui≤n, vi≠uivi≠ui) — the description of the ii-th edge. The graph should contain no multiple edges — for each pair (x,y)(x,y) you output, you should output no more pairs (x,y)(x,y) or (y,x)(y,x).

Examples input Copy

3
2 2 2

output Copy

YES 2
2
1 2
2 3

input Copy

5
1 4 1 1 1

output Copy

YES 2
4
1 2
3 2
4 2
5 2

input Copy

3
1 1 1

output Copy

NO

Note

Here are the graphs for the first two example cases. Both have diameter of 22.

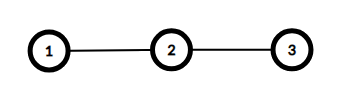d1=1≤a1=2d1=1≤a1=2

d2=2≤a2=2d2=2≤a2=2

d3=1≤a3=2d3=1≤a3=2

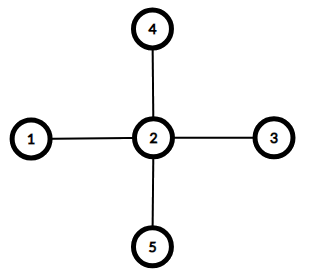d1=1≤a1=1d1=1≤a1=1

d2=4≤a2=4d2=4≤a2=4

d3=1≤a3=1d3=1≤a3=1

d4=1≤a4=1

 

這個題無語，自己打比賽的時候看錯題，求成最短的了，mdzz。。。

直接構造一條最長鏈就可以。從大到小連，為1的兩邊最多能連2個，其他的中間連，然後就可以了。

 

程式碼:

 1 //D
 2 #include<iostream>
 3 #include<cstdio>
 4 #include<cstring>
 5 #include<algorithm>
 6 #include<bitset>
 7 #include<cassert>
 8 #include<cctype>
 9 #include<cmath>
10 #include<cstdlib>
11 #include<ctime>
12 #include<deque>
13 #include<iomanip>
14 #include<list>
15 #include<map>
16 #include<queue>
17 #include<set>
18 #include<stack>
19 #include<vector>
20 using namespace std;
21 typedef long long ll;
22 typedef long double ld;
23 typedef pair<int,int> pii;
24 
25 const double PI=acos(-1.0);
26 const double eps=1e-6;
27 const ll mod=1e9+7;
28 const int inf=0x3f3f3f3f;
29 const int maxn=500+10;
30 const int maxm=100+10;
31 #define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
32 
33 int n,m,t,p,ans;
34 int d[maxn*2],first[maxn*2],v[maxn*2],w[maxn*2],nextt[maxn*2];
35 
36 struct node{
37     int p,d;
38 
39     bool operator <(const node &a)const{
40         return d<a.d;
41     }
42 
43 }a[maxn];
44 
45 vector<pair<int,int> > ve;
46 
47 ll pre[maxn];
48 
49 int main()
50 {
51     int n;
52     cin>>n;
53     int flag=0;
54     for(int i=1;i<=n;i++){
55         cin>>a[i].d,a[i].p=i;
56         if(a[i].d!=1)flag=1;
57     }
58     if(flag==0) {cout<<"NO"<<endl;return 0;}
59     sort(a+1,a+1+n);
60     for(int i=1;i<=n;i++)
61         pre[i]=pre[i-1]+a[i].d;
62     int i=n-1,con=n,tail=n,len=0,flag1=0,flag2=0;
63     while(1){
64         if(a[con].d&&a[i].d) {ve.push_back(make_pair(a[con].p,a[i].p));a[con].d--;a[i].d--;con--;i--;len++;}
65         else if(!a[con].d&&flag1==0) {ve.push_back(make_pair(a[tail].p,a[i].p));a[tail].d--;a[i].d--;i--;len++;flag1=1;if(a[tail].d==0) tail--;}
66         else{
67             if(a[tail].d!=0) {ve.push_back(make_pair(a[tail].p,a[i].p));a[tail].d--;a[i].d--;i--;if(a[tail].d==0) tail--;}
68             else {flag2=1;break;}
69     }
70         if(i==0) break;
71     }
72     if(flag2==1) {cout<<"NO"<<endl;return 0;}
73     vector<pair<int,int> >::iterator it;
74     cout<<"YES "<<len<<endl;
75     cout<<ve.size()<<endl;
76     for(it=ve.begin();it!=ve.end();it++){
77         cout<<(*it).first<<" "<<(*it).second<<endl;
78     }
79 }