M - Atlantis HDU - 1542 -掃描線-面積並
阿新 • • 發佈:2018-12-01
-
M - Atlantis
- HDU - 1542
- 感謝:https://www.cnblogs.com/scau20110726/archive/2013/03/21/2972808.html
- 1.矩形比較多,座標也很大,所以橫座標需要離散化(縱座標不需要),熟悉離散化後這個步驟不難,所以這裡不詳細講解了,不明白的還請百度
- 2.重點:掃描線法:假想有一條掃描線,從左往右(從右往左),或者從下往上(從上往下)掃描過整個多邊形(或者說畸形。。多個矩形疊加後的那個圖形)。如果是豎直方向上掃描,則是離散化橫座標,如果是水平方向上掃描,則是離散化縱座標。下面的分析都是離散化橫座標的,並且從下往上掃描的。
- 掃描之前還需要做一個工作,就是儲存好所有矩形的上下邊,並且按照它們所處的高度進行排序,另外如果是上邊我們給他一個值-1,下邊給他一個值1,我們用一個結構體來儲存所有的上下邊
- 接著掃描線從下往上掃描,每遇到一條上下邊就停下來,將這條線段投影到總區間上(總區間就是整個多邊形橫跨的長度),這個投影對應的其實是個插入和刪除線段操作。還記得給他們賦的值1或-1嗎,下邊是1,掃描到下邊的話相當於往總區間插入一條線段,上邊-1,掃描到上邊相當於在總區間刪除一條線段(如果說插入刪除比較抽象,那麼就直白說,掃描到下邊,投影到總區間,對應的那一段的值都要增1,掃描到上邊對應的那一段的值都要減1,如果總區間某一段的值為0,說明其實沒有線段覆蓋到它,為正數則有,那會不會為負數呢?是不可能的,可以自己思考一下)。
- 每掃描到一條上下邊後並投影到總區間後,就判斷總區間現在被覆蓋的總長度,然後用下一條邊的高度減去當前這條邊的高度,乘上總區間被覆蓋的長度,就能得到一塊麵積,並依此做下去,就能得到最後的面積
- (這個過程其實一點都不難,只是看文字較難體會,建議紙上畫圖,一畫即可明白,下面獻上一圖希望有幫組)
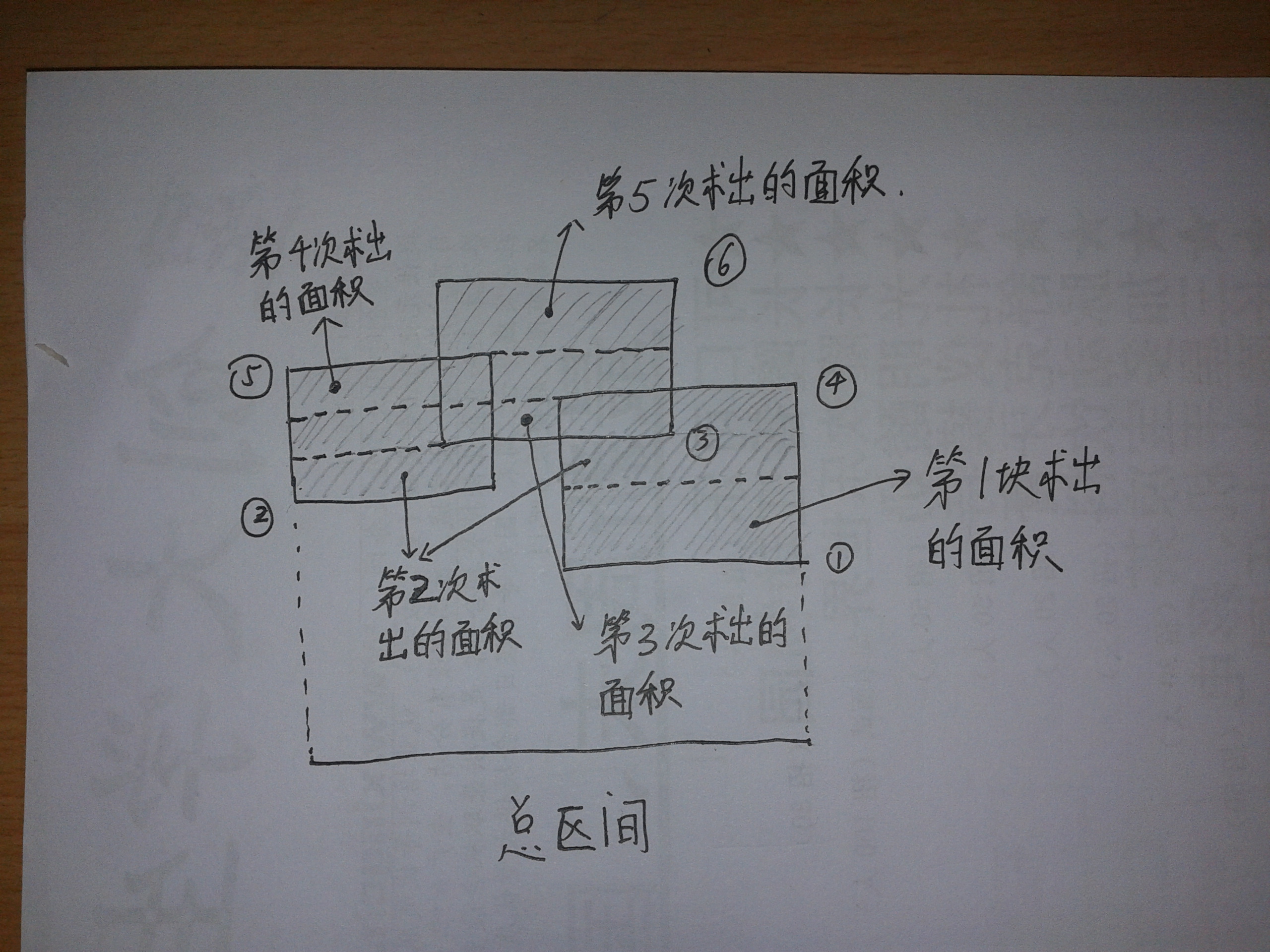
- 注意線段樹節點維護的是(i-i+1)一小線段為節點
-
#include<bits/stdc++.h> using namespace std; const int maxn = 210; struct edg { double l,r,h; int flag; bool operator<(const edg &b)const { return h<b.h; } } edge[maxn*2]; struct node { int l,r,lazy; double len; } tree[maxn*4]; double ls[maxn*2],ans; int cnt,n,NUM,nums; void add(double x1,double x2,double y,int id) { edge[cnt].flag=id; edge[cnt].h=y; edge[cnt].l=x1; edge[cnt++].r=x2; } void build(int root,int l,int r) { tree[root].l=l; tree[root].r=r; tree[root].len=0; tree[root].lazy=0; if(l==r)return ; int mid=(l+r)/2; build(root*2,l,mid); build(root*2+1,mid+1,r); } void pushup(int root) { if(tree[root].lazy) tree[root].len=ls[tree[root].r+1]-ls[tree[root].l]; else if(tree[root].l==tree[root].r) tree[root].len=0; else tree[root].len=tree[root*2].len+tree[root*2+1].len; } void updata(int root,int l,int r,int val) { if(tree[root].l==l&&tree[root].r==r) { tree[root].lazy+=val; pushup(root); return ; } int mid=(tree[root].l+tree[root].r)/2; if(l>mid) updata(root*2+1,l,r,val); else if(mid>=r) updata(root*2,l,r,val); else { updata(root*2,l,mid,val); updata(root*2+1,mid+1,r,val); } pushup(root); } int main() { while(scanf("%d", &n)) { if(n==0)break; ans=cnt=nums=0; for(int i=0; i<n; i++) { double x1,y,x2,y2; scanf("%lf%lf%lf%lf",&x1,&y,&x2,&y2); add(x1,x2,y,1); add(x1,x2,y2,-1); ls[nums++]=x1; ls[nums++]=x2; } sort(edge,edge+cnt); sort(ls,ls+nums); int m=unique(ls,ls+nums)-ls; build(1,0, m-1); for(int i=0; i<cnt-1; i++) { int l=lower_bound(ls,ls+m,edge[i].l)-ls; int r=lower_bound(ls,ls+m,edge[i].r)-ls; updata(1,l,r-1,edge[i].flag); ans+=(edge[i+1].h-edge[i].h)*tree[1].len; } printf("Test case #%d\n", ++NUM); printf("Total explored area: %.2f\n\n", ans); } return 0; }
