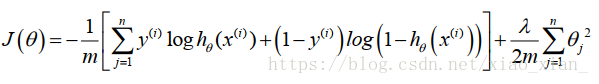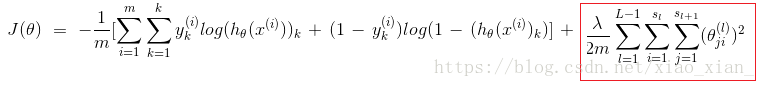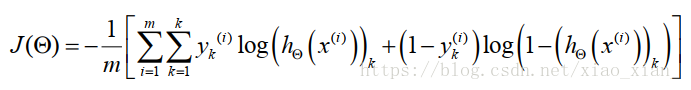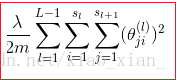機器學習中最重要的三個部分為網路結構、損失函式、優化策略。

而其中以損失函式最難以理解，主要原因是需要較強的數學知識，其中用的最多的就是引數估計。

所謂引數估計就是：對未知引數θ進行估計時，在引數可能的取值範圍內選取，使“樣本獲得此觀測值”的概率最大的引數作為θ的估計，這樣選定的有利於”的出現。

在機器學習指的就是，在已知資料集（結果）和模型（分佈函式）的情況下，估計出最適合該模型的引數。 

logistic迴歸的代價函式形式如下：

該代價函式就是通過--最大似然估計 出來的

最大似然估計 

 定義：最大似然估計(Maximum likelihood estimation)就是指，在已知樣本結果

 最大似然估計的重要前提：訓練樣本的分佈能代表樣本的真實分佈。每個樣本集中的樣本都是所謂獨立同分布的隨機變數 (iid條件)，且有充分的訓練樣本。

最大似然估計提供了一種給定觀察資料來評估模型引數的方法，即：“模型已定，引數未知”。通過若干次試驗，觀察其結果，利用試驗結果得到某個引數值能夠使樣本出現的概率為最大，則稱為最大似然估計。

數學定義：

 求解步驟：

 舉例：

 Logistic迴歸代價函式的推導：

神經網路代價函式--詳解

Logistic邏輯迴歸的代價函式

以邏輯迴歸為基礎的神經網路的代價函式

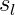
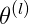
k：輸出單元個數即classes個數，L：神經網路總層數，：第L層的單元數（不包括偏置單元），：表示第L層邊上的權重即引數。 

逐步分解解析：

這一部分相比原來的公式，增加了一個關於K的累加。這裡的 K 代表著分類的數量，對應著輸出層輸出結果的數量4。

　　這裡的下標 k ，就是計算第 k 個分類的意思。

　　也就是說，我們需要求得的引數， 應該對每一個分類計算代價函式，並使得加總之後的結果最小。

這部分是正則化項  稱為正則化係數，表示每層神經元的個數
是對每一個 θ 的平方進行累計。三個累加的含義。

最裡層的迴圈j迴圈所有的行（由層的啟用單元數決定）；對某一層的每一行進行加總：

迴圈i則迴圈所有的列，由該層（層）的啟用單元所決定；對某一層的每一列進行加總：

 對每一層進行加總：

正則化： 

         ————改善或減少過擬合問題（保留所有特徵，但減少引數的大小）

正則化基本方法：在一定程度上減少高次項的係數，使之接近於0。

                            修改代價函式，即給高次項設定一些懲罰。

                            如果不知道哪些特徵需要懲罰，將對所有的特徵進行懲罰 。（不對進行懲罰）

                            正則化係數不宜太大，太大會使    造成欠擬合的現象

最大似然函式的博文來自：https://blog.csdn.net/The_lastest/article/details/78759837

損失函式原博文：https://blog.csdn.net/The_lastest/article/details/78761577

神經網路的代價函式博文參考：https://blog.csdn.net/The_lastest/article/details/77979624

                                                 https://blog.csdn.net/qq_32506555/article/details/78128820