卷積層

CNN中卷積層的作用：

CNN中的卷積層，在很多網路結構中會用conv來表示，也就是convolution的縮寫。

卷積層在CNN中扮演著很重要的角色——特徵的抽象和提取，這也是CNN區別於傳統的ANN或SVM的重要不同。

對於圖片而言，圖片是一個二維度的資料，我們怎樣才能通過學習圖片正確的模式來對於一張圖片有正確的對於圖片分類呢？這個時候，有人就提出了一個觀點，我們可以這樣，對於所有的畫素，全部都連線上一個權值，我們也分很多層，然後最後進行分類，這樣也可以，但是對於一張圖片來說，畫素點太多，引數太多了。然後就有人提出來，我們只看一部分怎麼樣，就是對於一張圖片來說，我們只看一個小視窗就可以了，對於其他的地方，我們也提供類似的小視窗，我們知道，當我們對圖片進行卷積的時候，我們可以對圖片進行很多操作，比如說圖片整體模糊，或者是邊緣的提取，卷積操作對於圖片來說可以很好的提取到特徵，而且通過BP誤差的傳播，我們可以根據不同任務，得到對於這個任務最好的一個引數，學習出相對於這個任務的最好的卷積核，之所以權值共享的邏輯是：如果說一個卷積核在圖片的一小塊兒區域可以得到很好的特徵，那麼在其他的地方，也可以得到很好的特徵。

填充（Padding）

valid：也就是不填充。
same：在影象邊緣填充，使得輸入和輸出大小相同。

不採用padding的後果：

• 邊緣資訊取樣小
• 輸出影象變小

而paddding通常可以保證卷積過程中輸入和輸出的維度是一樣的。它還可以使影象邊緣附近的幀對輸出的貢獻和影象中心附近的幀一樣。

假設輸入的影象大小為：n*n，過濾器大小為f*f，填充的大小為p，步長為s；

那麼，輸出的大小為

①假設步長stride大小為1，並且沒有填充，則輸出為：

②假設步長stride大小為1，並且填充的大小為p，則輸出為：

根據以上公式可以看出，加入我們沒有填充的話，輸出的大小會小於輸入的大小，然而在實際中，我們往往希望，輸出的大小能夠與輸入的大小相同，於是，我們可以得到下面這個等式：

解得：

由以上式子可知，當f為奇數時，填充的大小也隨之確定。也許你會問，難道過濾器的大小一定要為奇數嗎？理論上，f為偶數也是可以的。但是在實際工程應用中，f一般會取奇數（很多情況下取3），原因如下：

• 若為偶數，則有可能是不對稱填充，顯然我們不喜歡這樣的操作
• 奇數有中心畫素點，便於我們定位過濾器的位置

步長（Stride）

③假設步長大小為s，並且填充的大小為p，則輸出為：

需要注意的是，當結果不為整數時，我們一般採取下取整操作！

池化（Pooling）：卷積層是對影象的一個鄰域進行卷積得到影象的鄰域特徵，池化層就是使用pooling技術將小鄰域內的特徵點整合得到新的特徵。

優點：

• 顯著減少引數數量
• 池化單元具有平移不變性

在實際中經常使用的是最大池化。

卷積神經網路減少引數的手段：

1）稀疏連線

一般認為人對外界的認知是從區域性到全域性的，而影象的空間聯絡也是區域性的畫素聯絡較為緊密，而距離較遠的畫素相關性則較弱。因而，每個神經元其實沒有必要對全域性影象進行感知，只需要對區域性進行感知，然後在更高層將區域性的資訊綜合起來就得到了全域性的資訊。網路部分連通的思想，也是受啟發於生物學裡面的視覺系統結構。視覺皮層的神經元就是區域性接受資訊的（即這些神經元只響應某些特定區域的刺激）。如下圖所示：左圖為全連線，右圖為稀疏連線。

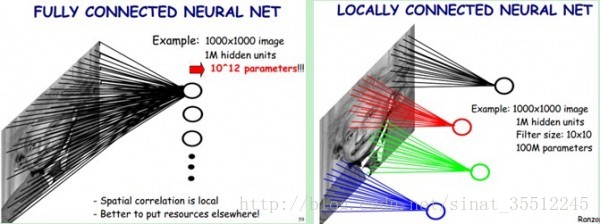
在上右圖中，假如每個神經元只和10×10個畫素值相連，那麼權值資料為1000000×100個引數，減少為原來的千分之一。而那10×10個畫素值對應的10×10個引數，其實就相當於卷積操作。

2）引數共享

但其實這樣的話引數仍然過多，那麼就啟動第二級神器，即權值共享。在上面的區域性連線中，每個神經元都對應100個引數，一共1000000個神經元，如果這1000000個神經元的100個引數都是相等的，那麼引數數目就變為100了。

怎麼理解權值共享呢？我們可以這100個引數（也就是卷積操作）看成是提取特徵的方式，該方式與位置無關。這其中隱含的原理則是：影象的一部分的統計特性與其他部分是一樣的。這也意味著我們在這一部分學習的特徵也能用在另一部分上，所以對於這個影象上的所有位置，我們都能使用同樣的學習特徵。

更直觀一些，當從一個大尺寸影象中隨機選取一小塊，比如說 8×8 作為樣本，並且從這個小塊樣本中學習到了一些特徵，這時我們可以把從這個 8×8 樣本中學習到的特徵作為探測器，應用到這個影象的任意地方中去。特別是，我們可以用從 8×8 樣本中所學習到的特徵跟原本的大尺寸影象作卷積，從而對這個大尺寸影象上的任一位置獲得一個不同特徵的啟用值。

如下圖所示，展示了一個33的卷積核在55的影象上做卷積的過程。每個卷積都是一種特徵提取方式，就像一個篩子，將影象中符合條件（啟用值越大越符合條件）的部分篩選出來。

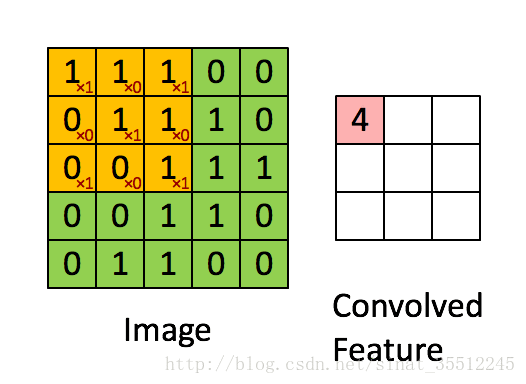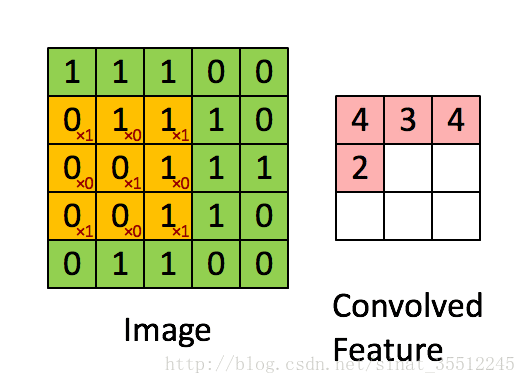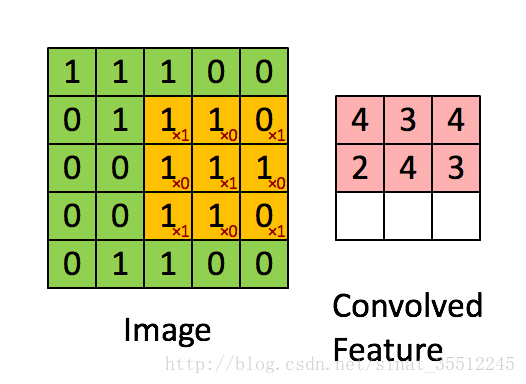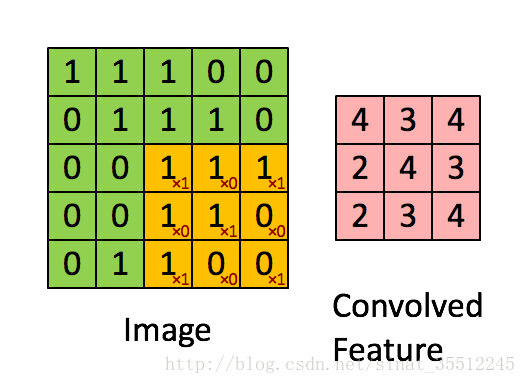
參考文獻：