支援向量機_斯坦福CS229_學習筆記

Part V 支援向量機（Support Vector Machines）

支援向量機（Support Vector Machines）被認為是最好的監督學習演算法。作為解決二分類問題而被提出。接下來，我想結合自己的理解，來講講SVM的故事。故事章節相對而言較多，結合目錄來看會更清晰一些。

Part V 支援向量機（Support Vector Machines）

Chapter 6 最優邊界分類器的對偶問題求解

Chapter 7 SVM優化之核函式

Chapter 8 SVM優化之軟間隔分類器

Chapter 1 前言

SVM的故事得從間隔（margin）這個概念講起。還記得在邏輯迴歸中，我們是怎麼進行分類的嗎？我們相當於畫了一條h(x)=0.5的線進行判斷。當h(x)>0.5，認為是正樣本，否則視為負樣本。這樣一刀切判斷的方式，自然而然的問題是對於所有h(x)>0.5都一視同仁了。因為無論是直覺還是邏輯都告訴我們，當h(x)越接近於1時，正樣本的可能性也就越高；反之，當h(x)越接近於0，那麼負樣本的可能性也就越高；而在h(x)約為0.5時，是最模稜兩可的時候。因此一個改進的地方便是需要使用某種方式去衡量這種置信的程度。而考慮了這種置信程度的事兒，正是SVM所要做的。

再觀察下面這張圖：

一條直線（決策邊界）將樣本分開。假設X代表正樣本，O為負樣本。此時A、B、C三點都被劃分為了正樣本，即使這樣，正樣本與正樣本之間扮演的角色是不同的。A更像是正樣本，而C最不像正樣本。也就是A是正樣本的置信程度比C高，但是在邏輯迴歸中，訓練的時候，我們卻將A、B、C三點一視同仁。如何體現A、B、C三點在訓練之中扮演的角色，這是SVM的突破口。

為了便於接下來的理解，這裡直接給出最簡單的SVM的例子。

參照上圖，SVM的思想便是：尋找一條邊界（圖中實線），使得正類別和負類別中距離該邊界最近的點（虛線上的點，這些點也稱為支援向量）到邊界的距離最遠。也就是說，在各個類別的樣本中，只有支援向量對於該邊界的形成有影響。話不算拗口，思路也算清晰，但是SVM的故事卻很深很長。

Chapter 2 符號

為了便於SVM的推導，需要做一些記號的更改。

（1）負正樣本不再用（0，1）表示，而是用（-1，1）表示。

（2）我們所有求得的劃分的超平面，也就是決策邊界記為 $\bg_white \small g(x)=w^{\top }x+b$ 。即相對於之前的線性迴歸與邏輯迴歸：

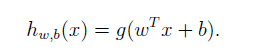
（3）採用如下方式進行判斷：當有判斷資料來時，帶入上式。若結果大於0，即判斷為正樣本1；否則判斷為負樣本-1。這樣定義看上去有點像感知機演算法。

Chapter 3 函式間隔和幾何間隔

那麼如何體現同一類別中不同樣本的差異呢？也就是說，SVM中的這個距離量度該怎麼衡量呢。函式間隔（Functional Margin）和幾何間隔（Functional Margin）為此提供了一個思路。

對於一個訓練樣本 $(x^{i},y^{i})$ ，相應的引數w和b，定義這個樣本的函式間隔如下：

有兩個細節需要注意：

（1）函式間隔始終為非負。當該樣本屬於正樣本時，即 $y^{i}=1$ ，那麼要使函式間隔變大，即要使 $w^{\top }x+b$ 為一個較大的正實數；同樣，當樣本屬於負樣本時，即 $y^{i}=-1$ ，那麼要使函式間隔變大，即要使 $w^{\top }x+b$ 為了一個較大的負實數。

（2）由細節（1）可知，利用函式間隔我們可以判斷分類器是否分類正確，如果 $y^{i}(w^{\top }x+b)>0$ ，那麼就認為分類正確。不僅如此，當函式間隔越大時，我們越有理由相信，這個分類結果越正確。

有了單個樣本的函式間隔，假設樣本集有m個樣本，下面給出整個樣本集S的函式間隔定義。

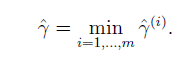
契合SVM的思想，將整個樣本中最小的函式間隔定義為該樣本的函式間隔，

似乎函式間隔可以作為判別的依據了，那麼我們只要使函式間隔越大，分類器效果應該就會更好。其實不然，因為函式間隔存在一個致命的地方。

再回頭看我們定義的判別準則， $w^{\top }x+b>0$ 判斷為正樣本，反之為負樣本。那麼你會發現滿足 $w^{\top }x+b=0$ 的這個點（w，b）至為重要。如果以使函式間隔最大為優化目標，那麼會存在一種情況是，當成比例的變化w和b時，也就是變化為2w，2b或者是3w，3b時，雖然函式間隔變大了，但是 $w^{\top }x+b$ 的零點仍然是沒有變化的，也就是說在這種情況下，對於優化分類器是沒有作用的，分類器仍然是選用與之前的相同的 $w^{\top }x+b$ 的零點作為判斷。那麼以函式間隔作為優化判斷的方式，便會使訓練時走入歧途。

看來函式間隔並不是一個很好的方式啊。但是你可能會想到，解決這個問題最直接的思路就是，把w和b單位化不就得了。沒錯，這就是幾何間隔的思路。

既然是幾何間隔，那麼其故事就得從幾何出發了。

觀察上圖，決策邊界 $w^{\top }x+b=0$ 為實線所示。那麼w作為法向量，其方向自然於邊界正交。那麼單位法向量即為 $w/\left \| w \right \|$ 。正樣本A的座標 $x^{(i)}$ ，這裡二維平面，那麼 $x^{(i)}$ 就可用x0和x1表示。A點沿著法向量方向在決策邊界的投影點為B。將AB的長度定義為幾何間隔，即為 $\gamma ^{i}$ （注意與函式間隔記號相比，頭上少了個小三角）。注意到A點座標為 $x^{(i)}$ ，那麼B的座標即為 $x^{i}-\gamma ^{i}*w/\left \| w \right \|$ ，又因為B點位於決策邊界 $w^{\top }x+b=0$ 之上，因此將B點座標帶入，可得

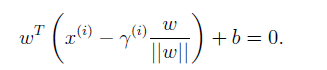
由此方程解出幾何間隔，得

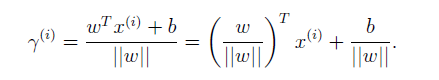
這是A為正樣本的情況，參照函式間隔的定義，定義對於某樣本的幾何間隔如下：

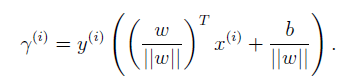
注意到當 $\left \| w \right \|=1$ 時，幾何間隔變為函式間隔。幾何間隔作為函式間隔的升級版，解決了函式間隔的問題。在幾何間隔的基礎上，就可以對w和b進行任意縮放了。為了契合SVM思想，給出整個樣本集S的幾何間隔定義，同樣是選取樣本中最小的幾何間隔作為樣本集的幾何間隔。

Chapter 4 最優邊界分類器

幾何間隔完成了SVM思想的第一步，即定義了距離量度，並尋找到樣本中距離決策邊界最近的樣本（即尋找到了支援向量），那麼接下來要做的便是，使支援向量跟決策邊界的距離最遠，即使樣本集的幾何間隔最大（對於分類的置信程度也就越高）。

在此，假設我們的訓練集線性可分，可以將優化問題定義如下。優化的目標是使樣本集的幾何間隔最大。

順水推舟，在得到樣本集的幾何間隔 $\gamma$ 的基礎之上，我們要尋找的便是一組（w，b）使得 $\gamma$ 最大。這個問題顯得如此抽象，無從下手，顯然我們要做一些改進。還記得函式間隔和幾何間隔的關係嗎？

$\gamma =\frac{\tilde{\gamma }}{\left \| w \right \|}$

將函式間隔替代幾何間隔，可將優化目標改寫為：

還不夠，仍然不好求解。繼續改進。注意到，在函式間隔中提到，對於函式間隔而言，將w，b成比例縮放不會影響決策的判斷，因為零點是不變的（忘記了可以參見上文）。那麼我們就縮放w和b唄，反正也不影響決策結果，為了方便，縮放w，b直到函式間隔為定值1，反正也沒啥關係。那麼優化目標就由 $\frac{\tilde{\gamma }}{\left \| w \right \|}$ 變為 $\frac{1}{\left \| w \right \|}$ ；又可以注意到 $max \frac{1}{\left \| w \right \|}$ 與 $min \frac{1}{2}\left \| w \right \|$ 是一樣的。因此更改優化目標為：

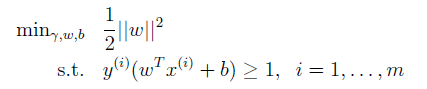
這樣就將之前抽象的問題轉化為二次凸優化問題了。直接的方式便是利用線性規劃進行解決。但是，如果這樣的話，SVM這個故事豈不是就不精彩了？接下來會介紹另一個思路來解此優化問題，並且可以在其中利用核函式的思想，進行維度的擴充，使SVM的效能更強。為了引出這種方法，接下來暫且拋開以上內容，先講講何為拉格朗日對偶問題。

Chapter 5 拉格朗日對偶問題

暫且先不管以上內容。先看看拉格朗日對偶問題（Lagrange Duality）是什麼。

引入包含限制條件的多元函式求極值中會用到拉格朗日乘數法作為拋磚引玉。首先，還是先定義了一個優化問題，可以看做一個被限制條件約束的求解極值的問題。這裡假設w是n維引數向量，該問題被 $\iota$ 個條件限制。

這個問題可以利用拉格朗日乘數法進行求解。如果對於拉格朗日乘數法求解極值沒有印象的話，沒有關係，接下來我們來走一下流程。首先構建拉格朗日方程，其中 $\beta _{i}$ 為待求解引數，也稱為拉格朗日乘子（Lagrange multipliers.）。

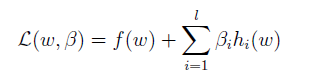
由此方程分別對於w和 $\beta _{i}$ 求偏導，並令其結果為0：

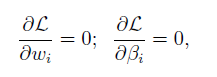
得到n+ $\iota$ 個方程，聯立求解這n+ $\iota$ 個方程，即可解出w。

基於上述內容，我們對於拉格朗日方程進行推廣。假設要解決的問題不僅包括等式h（w）的約束，而且還包括不等式g（w）的約束。這個問題也稱為原始優化問題，簡稱原始問題（primal optimization problem）。形式如下：

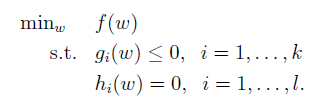（5.1）

為了解決此問題，構建廣義拉格朗日方程。

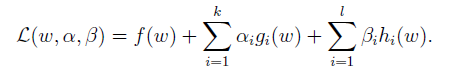
在這裡，相比較之前，拉格朗日乘子擴充了：k個 $\alpha _{i}$ 和 $\imath$ 個 $\beta _{i}$ 。

接下來，引入一個新定義，下標p代表‘primal’：

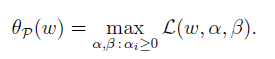（5.2）

那麼可以得到 $\theta _{\rho }(w)$ 和 f（w）存在以下關係：

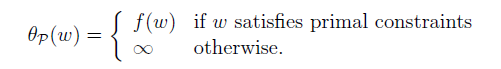
這裡的原始限制條件（primal constraints）指的是原始問題中對於w的限制條件，也就是：

你可以試下當 $g_{i}(w)>0$ 或者 $h_{i}(w)\neq 0$ 時， $\theta _{\rho }(w)$ 的形式如何，就會明白 $\theta _{\rho }(w)$ 和 f（w）的關係了。用 $\theta _{\rho }(w)$ 替換f（w），那麼就可以得到：

$min_{w} f(w)=min_{w}\theta _{\rho}(w)=min_{w} max_{\alpha ,\beta ;\alpha _{i}\geq 0}L(w,\alpha ,\beta )$

那麼這又怎麼解呢？暫且不管，假設其的解為p*，即 $p^{*}=min_{w}\theta _{\rho }(w)$ 。

接著定義，這裡下標D的意思為’dual’，該定義與（5.2）相呼應。

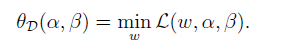
在以上定義的基礎上，定義對偶優化問題（dual optimization problem），簡稱對偶問題。注意與原始問題的區別啊。也就是改變了求最大和求最小的順序。

同樣，定義對偶問題的解d*。 $d^{*}=max_{\alpha ,\beta ;\alpha _{i}\geq 0}\theta _{D }(w)$ 。

由此，我們可以得到兩個問題解之間的聯絡。

如何理解呢？自然來理解，最小值裡面的最大值小於等於最大值裡面的最小值，沒問題。

看到這裡或許你就明白了，當原始問題不好求解的時候，可以轉換為其的對偶問題進行求解。那麼當滿足什麼條件時，原始問題可以轉化為其對偶問題，也就是說d*=p*呢？這就是接下來要說的KKT條件。當滿足KKT（Karush-Kuhn-Tucker）條件時，兩個問題的解相同，理所當然就可以將一個問題轉化為另一個問題進行求解了。

何謂KKT條件呢？回頭看看（5.1）定義的原始問題。假設f（w）， $g_{i}(w)$ 為凸函式，且 $h_{i}(w)$ 為線性函式（講義中註明 $h_{i}(w)$ 為仿射，這裡理解為線性就好）；並且存在著一些 $g_{i}(w)$ 使得 $g_{i}(w)<0$ （看完故事，你就明白這些就是要找的支援向量了）。參照上文，給出KKT條件，其中w*為原始問題的解，而a*，b*為其對偶問題中引數的解。

第1行與第2行，容易明白，即保證拉格朗日平穩，最優解處偏導為0。第4行的定義與第5行的定義都與原始問題中的限制條件相契合。重點關注第3行。第3行也稱為KKT對偶互補條件（dual Complementary condition），其暗示著若 $\alpha _{i}^{*}>0$ ，則 $g_{i}(w^{*})=0$ ，通過這個條件的限制，就幫助我們尋找到支援向量了。第1、2、4、5行都很直接，第3行可以看作是對於第4行和第5行的進一步約束。因為公式直接來源於講義沒有更改（可能是為了美觀所以如此排列），但是我覺得將第3行放置在最後，可能會更便於理解。

真是一環扣著一環啊。趁熱打鐵，返回故事的主線。

Chapter 6 最優邊界分類器的對偶問題求解

回到故事主線。在上文的基礎上，解決之前遺留優化問題的思路浮出水面：我們可將原始問題轉為對偶問題進行求解。還記得在前文（C4），我們提出下面優化問題：

（6.1）

結合（5.1），這裡由於比較（5.1）來說沒有等式約束，所以 $h_{i}(w)$ 就不寫進去了。觀察到不等式的約束，移項稍作修改，我們可以這麼定義 $g_{i}(w)$ 。

這裡相當於每個樣本都給分類器提供了一個限制條件。

如果你沒有忘記的話，這裡的1代表的是樣本集函式間隔為1，即某一樣本的函式至少為1。結合KKT中的對偶互補條件可知，若 $\alpha _{i}>0$ ，那麼該訓練樣本的函式間隔為1。但是注意反之確不一定成立。這是個小細節，但是感覺大家都沒有深究一下，對於函式間隔為1的點，其對應著的 $\alpha _{i}$ 不一定大於0啊，那麼便會存在著一種情況即所有的支援向量對應著的 $\alpha _{i}$ 的值都為0，那麼此時結合（6.3）式w便為0，結合（6.5）b也為0，此時的決策邊界即為x=0。對於其他函式間隔大於1的點來說，同樣由於KKT互補條件的限制，使得其 $\alpha _{i}$ 為0。也就是說真正對於優化起限制作用的是那些函式間隔為1的點（也就是支援向量）。從這裡你就可以發現，KKT互補條件的其中之一作用便是找到支援向量，從而只使支援向量對於優化目標具備限制作用。

在（6.1）的基礎上構建拉格朗日方程：

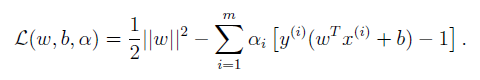（6.2）

注意由於只有不等式約束，所以拉格朗日乘子只有 $\alpha _{i}$ 。下一步便是將（6.1）轉化為對偶問題的形式進行求解。

首先最小化（6.2）時，此時的引數為w和b。這一步可以直接對（6.2）中w和b求偏導，並另其偏導數為0進行求解。對w求偏導：

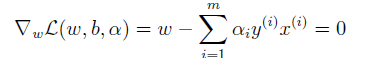
得

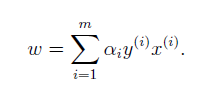（6.3）

接著對b求偏導得

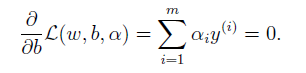（6.4）

將（6.3）帶入（6.2）得

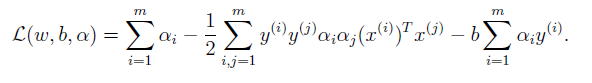
帶入（6.4）抵消最後一項得

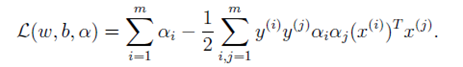
這就完成了對偶問題求解的第一步。整理以上限制條件，那麼可以得到求解的第二步如下所示：

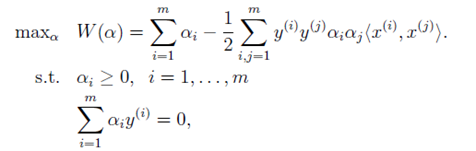
在這裡注意幾個細節：

（1）這裡先不給出如何求解此方程，因為會在下節插入一些內容。具體求解方式在之後會進行介紹。

（2）針對於整個問題來說，我們要求解的引數為w和b。當我們求解此方程得到a後，將其帶入（6.3）式，便可解出w。

（3）在這裡，大家也注意到了。我們將 $x^{(i)}^{\top }*x^{(j)}$ 寫成內積的形式 $\left \langle x^{(i)},x^{(j)} \right \rangle$ 。為什麼這麼寫，是為了方便應用核函式。一環扣一環，具體請見下一節內容。

（4）如果只針對上述問題，可以感性的給出引數b的求解結果。b的具體求解步驟參照C9。

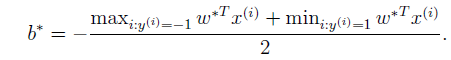
看圖說話會更明白一些。

要明白，b這個變數相當於該決策邊界的截距。那麼當w求出來之後，因為我們明白，該決策邊界總是在中間，距離兩端的支援向量一樣遠。引數b就是兩個分類中的支援向量對應著的平行於決策邊界的線（上、下兩條虛線）的截距的平均值。

好了，有了引數w和b，那麼當有一個數據需要判斷時，可以直接帶入方程 $w^{\top }x+b=0$ 進行判斷了。若結果大於0，即為正樣本，否則為負樣本。但是也有另一種判斷形式。將（6.3）式帶入 $w^{\top }x+b=0$ 可得：

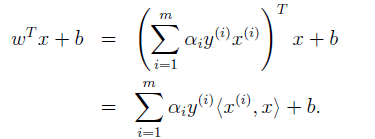
之所以這樣做的目的是在於，許多的 $\alpha _{i}$ 都為0，僅有支援向量對應著的 $\alpha _{i}$ 不為0，用 $\alpha _{i}$ 來進行判斷會減少不少的計算時間，因此會節省一些計算資源。

至此SVM的求解就差最後一步了。但是先不急繼續，SVM之所以強大，少不了對於其做的一些優化措施。接下來的兩節，會講述基於SVM演算法的優化。正如前文所述，SVM的故事很深很長，所以，讓我們繼續吧。

Chapter 7 SVM優化之核函式

在上一節的後部分，在處理 $x^{(i)}^{\top }*x^{(j)}$ 的時候，都寫成了內積形式 $\left \langle x^{(i)},x^{(j)} \right \rangle$ ，這也是為這章要闡述的核函式做一個鋪墊。如果你沒太注意，可以返回到一開始，當介紹SVM時，我們做了一個前提假設，即假設訓練集線性可分。那麼若是訓練集線性不可分呢？這便可以應用核函式進行解決。核函式的作用便是將低維特徵空間對映到高維，因此在低維空間不可分的問題就可能會在高維空間得到解決。

首先，讓我們看下什麼是特徵對映，例如假設x為一維特徵向量，經過如下函式 $\phi (x)$ 進行對映，便可從一維空間對映到三維空間。經過對映後便可以改變原有特徵的維度。

那麼核函式的所要做的便是將原本的特徵空間對映到更高維的特徵空間，這樣在低維特徵空間線性不可分的問題就可能會在高維特徵空間線性可分，從而使在低維空間線性不可分的問題得到解決。

由於在之前的演算法中，已經寫成了內積的形式，那麼要進行特徵對映，只需將 $\left \langle x^{(i)},x^{(j)} \right \rangle$ 替換為 $\left \langle \phi (x^{(i)}),\phi(x^{(j)}) \right \rangle$ 就行了。

根據某種特徵對映 $\phi (x)$ ，進一步我們可以定義核函式如下：

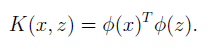
因此，在原有演算法所有使用 $\left \langle x^{(i)},x^{(j)} \right \rangle$ 的地方，我們相應替換為 $K(x^{(i)},x^{(j)})$ 。那麼演算法便可以根據對映後的特徵進行學習了。而且使用核函式的一個不錯的優勢在於，儘管對於對映函式 $\phi (x)$ 的計算會比較慢，但是實際計算中，我們不需要計算 $\phi (x)$ ，因此核函式的計算並不會過於增加計算量。讓我們看看以下例子便會明白了。

假設 $x,z\subseteq \mathbb{R}^{n}$ ，我們有一個核函式計算形式如下：

那麼這個核函式對應著的 $\phi (x)$ 是什麼形式呢？我們可以將其展開來看一下：

將其改寫為 $K(x,z)=\phi (x)^{\top }*\phi (z)$ 的形式，並設此時維度n=3。那麼 $\phi (x)$ 便有以下形式。可以看到以此種方式，將變數原有的3維特徵空間對映到了9維。

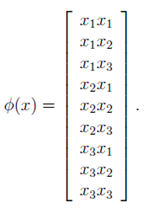
是不是很有趣，讓我們看看其他的核函式的形式。

（1）上述核函式更一般的形式。

（2）高斯核函式，貌似可以將特徵對映到無限維。不明覺厲。

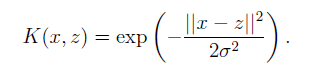
看到這裡，是否會感覺唐突，因為按照邏輯來講，應該是先給出對映函式 $\phi (x)$ ，然後再給出根據 $\phi (x)$ 相乘後的核函式的化解形式。但是卻先給出了核函式的化解形式，然後再利用其推出對映函式 $\phi (x)$ 。之所以這樣做，我覺得這更多的是數學和應用的原因吧，核函式在進行特徵對映的作用之外，而且還有一個要求是不能給之前的計算帶來太多的負擔。如果我們從對映函式 $\phi (x)$ 的角度出發去構造核函式，那感覺就像買彩票一樣，碰運氣，因為很難保證最終化解結果便於計算，而且實際上我們也不太關心 $\phi (x)$ 會是什麼樣子，想關心好像數學功底也不行，只要核函式能將特徵維度對映到高維空間就可以了，如果效果不好，那就換一個核函式繼續；但是如果從核函式的結果出發，去反推的話感覺還簡單一些。實際上，當我們從結果出發去構建時，只要有一個準則去幫助我們判斷這個核函式是否有效就可以了，就省去反推 $\phi (x)$ 的步驟，因為我們也不關心 $\phi (x)$ 具體是什麼。

這個準則就是Mercer定理：

在原有特徵維度可數，且樣本數量可數的前提下，核函式是有效核的充分必要條件是，該核函式對應著的核矩陣對稱半正定。

若樣本數量為m，核矩陣KK是一個m*m的矩陣，且 $KK(i,j)=K(x^{(i)},x^{(j)})$ 。

有了Mercer定理，好像就可以肆無忌憚的定義核函數了。

核函式作為一種優化手段，使SVM得效能得到極大提升。在其他一些演算法，核函式也能發揮不小的作用。怪不得都把這種優化手段稱為“kernel trick”。接下來會闡述SVM中的第二種優化手段。

Chapter 8 SVM優化之軟間隔分類器

雖然核函式將特徵空間由低維度對映到了高維度，但是仍有可能也會在高維度中線性不可分。並且有時候找到一個嚴格的決策邊界也並不是我們的目標。參照下圖。

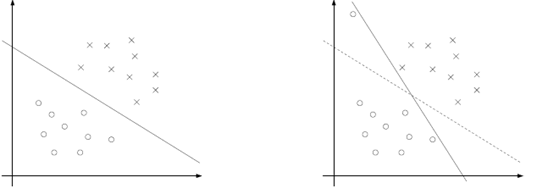
左圖是很理想的情況。實際情況中，往往會有許多噪聲，如右圖左上方的小圓。這些噪聲使得決策邊界有了不小改變，使得分類器得到的邊界很窄，這樣分類的置信程度就不高。但是實際情況中，我們還是希望決策邊界能夠不考慮噪聲的影響，仍然得到右圖中虛線的形式。這也就是軟間隔分類的思路。

既然如此，我們就加入一些正則化項，利用L1正則化，將優化的目標函式修改為：

也就是說，現在樣本的函式間隔被允許小於1。且對於函式間隔在 $1-\xi _{i}$ 的點，我們會給予 $C*\xi _{i}$ 的懲罰，從而使成本增加。引數C一方面的作用是使邊界擴大，一方面也在保證著大多數的樣本函式間隔至少為1。

結合前文內容，考慮軟間隔分類的情況下，構建拉格朗日方程得到：

此時，拉格朗日乘子不光有 $\alpha _{i}$ ，還有 $\gamma _{i}$ 。接著，推導其對偶方程得：

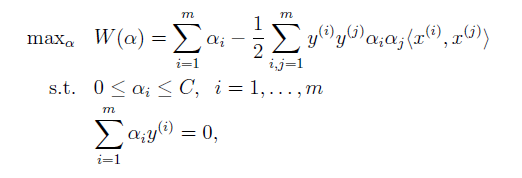
可以發現， $\gamma _{i}$ 抵消了；並且和之前唯一的區別在於，由 $0<=\alpha _{i}$ ，變為了 $0<=\alpha _{i}<=C$ 。

在這裡，相應的KKT互補條件也要進行更改。

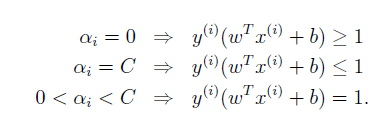
並且，在現在的情況下，得到的截距b的表示式也肯定和之前不一樣了。到了這一步，真的是萬事俱備，只欠東風了。到底解出對偶方程後的第一步後，第二步該怎麼解 $\alpha _{i}$ 。一鼓作氣，接下來就看看到底該怎麼解。

Chapter 9 SMO演算法

9.1 座標上升演算法

在講SMO（Sequential Minimal Optimization）的故事之前，我們先看看一個叫做座標上升（Coordinate Ascent）的演算法。暫且先拋開之前的內容。假設現在我們需要解決一個無條件限制的優化問題，如下：

之前其實也遇到過類似的問題，在前面兩講中，構建極大似然方程進行引數求解就是該問題的一個例子。那時，可以利用梯度上升或者牛頓法進行求解。類似的，利用座標上升法也可以對同樣問題進行求解。座標上升法如下所示：

同樣也是迭代的思路進行求解。思路如下：在每次迭代中，假設選取 $\alpha _{1}$ 進行迭代，那麼固定除 $\alpha _{1}$ 外的其他引數，此時w就可看作是 $\alpha _{1}$ 的函式，就是一個一元函式求極大值的問題，那麼令 $\frac{\partial w }{\partial \alpha _{1}}=0$ ，便得到 $\alpha _{1}$ 的新值，以此作為更新。接著選取 $\alpha _{2}$ 、 $\alpha _{3}$ ... $\alpha _{m}$ 進行同樣步驟。這樣便進行了一輪迭代。重複這輪迭代直到所有引數收斂。便完成了對於引數 $\alpha _{i}$ 的求解。與梯度上升作為對比，看看座標上升的圖。差別不言而喻。

從以上過程，我們可以發現，引數迭代的順序是從 $\alpha _{1}$ 到 $\alpha _{m}$ 。那麼自然而然就可以想到，可以通過修改引數的迭代順序，提高參數收斂的速度，例如每次選取使w增加最大的引數作為迭代的引數（雖然多增加了一些判斷和計算，但是會明顯提高收斂速度）。

9.2 SMO

現在回頭來看看SVM。還記得之前增加了軟間隔分類後的優化方程：

（9.1）

1998_[John Platt]_Sequential Minimal Optimization：A Fast Algorithm for Training Support Vector Machines這篇文章為我們求解SVM提供了一個方法，其基本思想便是在在座標上升演算法的思想上進行擴充套件。由於本人水平有限，對於這裡許多地方也可能存在著理解不到位，具體數學原理還是請大家參照上述論文。

在座標上升法中，我們固定了其餘引數，一次只對一個引數進行迭代，但是在（9.1）中，存在著約束條件： $\sum_{m}^{i=1}\alpha _{i}y^{(i)}=0$ 。因此當固定m-1個引數時，那麼最後一個引數也就被確定了，如（9.2）所示。當我們固定第2到第m個引數時，那麼第一個引數其實也被固定了。因此座標上升的方法還不能完全照搬過來。

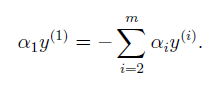（9.2）

注意到因為 $y^{(i)}\in (-1,1)$ ，所以 $y^{(i)}^{2}=1$ 。因此我們將（9.2）等式兩邊同時乘以 $y^{(1)}$ ，可將（9.2）寫作如下形式：

（9.3）

在SMO中，為了求解（9.1），我們同樣應用座標上升法的思想，但是我們通過一次更新兩個引數的方式來解決問題。SMO迭代過程可概括為：

讓我們看看一次迭代是怎麼進行的。

為了表示方便，假設這一次迭代選取 $\alpha _{1}$ 、 $\alpha _{2}$ 作為引數（如何啟發式選取將在下文介紹），固定其他引數得：

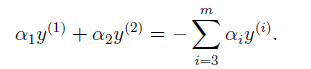
等式右端可看做一個常數，那麼我們用 $\zeta$ 代替，得：

（9.4）

同樣因為 $y^{(i)}\in (-1,1)$ ，經過移項，兩邊同時乘以 $y^{(1)}$ 後，那麼 $\alpha _{1}$ 可寫作如下形式：

支援向量機_斯坦福CS229_學習筆記

Part V 支援向量機（Support Vector Machines）

Chapter 1 前言

Chapter 2 符號

Chapter 3 函式間隔和幾何間隔

Chapter 4 最優邊界分類器

Chapter 5 拉格朗日對偶問題

Chapter 6 最優邊界分類器的對偶問題求解

Chapter 7 SVM優化之核函式

Chapter 8 SVM優化之軟間隔分類器

Chapter 9 SMO演算法

9.1 座標上升演算法

9.2 SMO

支援向量機_斯坦福CS229_學習筆記

生成學習演算法_高斯判別分析_樸素貝葉斯_斯坦福CS229_學習筆記

線性迴歸_邏輯迴歸_廣義線性模型_斯坦福CS229_學習筆記

EM演算法_斯坦福CS229_學習筆記

學習理論_斯坦福CS229_學習筆記

支援向量機（斯坦福大學課程講義Andrew Ng）

機器學習之支援向量機迴歸（機器學習技法）

斯坦福CS229機器學習筆記-Lecture8- SVM支援向量機之核方法 + 軟間隔 + SMO 演算法

斯坦福CS229機器學習筆記-Lecture6-多元伯努利事件模型+SVM支援向量機

機器學習筆記——支援向量機

《機器學習》周志華學習筆記第六章支援向量機（課後習題）python 實現

學習筆記（十）：使用支援向量機區分僵屍網路DGA家族

學習筆記（九）：使用支援向量機識別XSS

機器學習筆記（參考吳恩達機器學習視訊筆記）11_支援向量機

Andrew Ng 機器學習筆記 11 ：支援向量機(Support Vector Machine)

《統計學習方法》筆記七（2）支援向量機——線性支援向量機

機器學習實戰筆記5—支援向量機

【統計學習方法-李航-筆記總結】七、支援向量機

機器學習筆記之支援向量機

【機器學習筆記17】支援向量機

支援向量機_斯坦福CS229_學習筆記

Part V 支援向量機（Support Vector Machines）

Chapter 1 前言

Chapter 2 符號

Chapter 3 函式間隔和幾何間隔

Chapter 4 最優邊界分類器

Chapter 5 拉格朗日對偶問題

Chapter 6 最優邊界分類器的對偶問題求解

Chapter 7 SVM優化之核函式

Chapter 8 SVM優化之軟間隔分類器

Chapter 9 SMO演算法

9.1 座標上升演算法

9.2 SMO

相關推薦