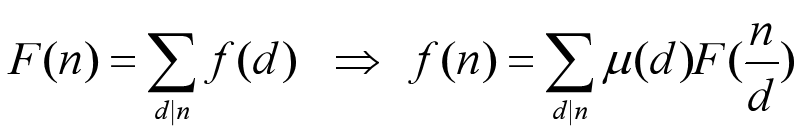
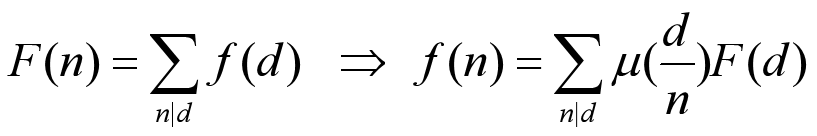
f(n)表示某一範圍內(x,y)=n的數對的數量，F(n)表示某一範圍內n|(x,y)的數對的數量
那麼直接求f(n)並不是很好求，而F(n)求起來相對無腦一些，我們可以通過對F(n)進行莫比烏斯反演來求得f(n)
線性篩μ模板：

void Prime(int N)
{
	mu[1]=1;int cnt=0;
	for(int i=2;i<=N;i++)
	{
		if(!v[i]) p[++cnt]=i,mu[i]=-1;
		for(int j=1,k;j<=cnt&&p[j]*i<=N;j++)
		{
			v[k=p[j]*i]=1
 
;
			if(i%p[j]==0) {mu[k]=0;break;}
			mu[k]=-mu[i];
		}
	}
}

$PS1\mathrm{：}for($

基本解題思路：列舉gcd

例題1：

求1<=i<=n, 1<=j<=m, gcd(i,j)=k 的(i,j)對數

該問題等價於求1<=i<=n/k (N), 1<=j<=m/k (M) gcd(i,j)=1 的(i,j)對數
$f(1)=\sum_{1|d}μ(\frac{d}1)*F(d)=\sum_dμ(d)*[\frac{N}d][\frac{M}d]$
由 $[\frac{N}d][\frac{M}d]$的取值是 $\sqrt{n}$級的，可以得出：

優化技巧一： 字首和+分塊優化

long long ans=0;
for(int i=1,j;i<=n;i=j+1)
{	
	j=min(n/(n/i),m/(m/i));
	ans+=1ll*(n/i)*(m/i)*(sum[j]-sum[i-1]);
}

$PS2：i=j+1不要寫成i++$
$PS3:不要忘乘1ll!!!$

例題2：

求1<=i<=n, 1<=j<=m, gcd(i,j)為質數 的(i,j)對數

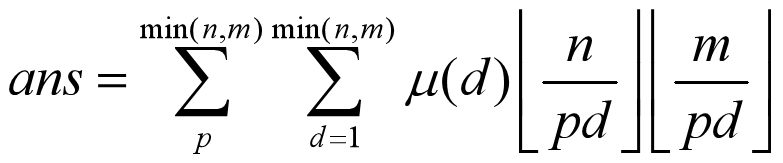
優化技巧二： 切換列舉次序

令上式的pd=T, 則有

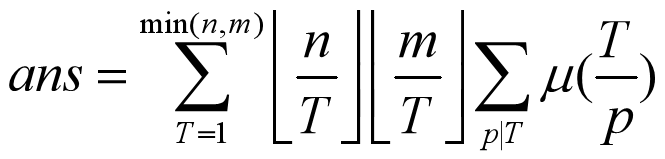
應用技巧一即可

例題3：

設 $d(x)$為 $x$的約數個數，給定N,M,T
求 $\sum_{i=1}^N\sum_{j=1}^Md(ij)$
N,M,T<=50000

題目解析見這裡：約數個數和 (莫比烏斯反演)
於是算不上技巧但是很神奇的技巧三：

技巧三：替換條件框

$[(x,y)==1] &lt;=&gt;\sum_{k|(x,y)}μ(k)$

例題3 程式碼

#include<cstdio>
#include<algorithm>
#define maxn 50005
using namespace std;
int T,n,m,p[maxn],mu[maxn],sum[maxn],mx[maxn];//線性篩約數個數
bool v[maxn];
void Prime(int N)
{
	mu[1]=sum[1]=1;int cnt=0;
	for(int i=2;i<=N;i++)
	{
		if(!v[i]){
			p[++cnt]=i,mu[i]=-1;
			sum[i]=mx[i]=2;
		}
		for(int j=1,k;j<=cnt&&p[j]*i<=N;j++)
		{
			v[k=p[j]*i]=1;
			if(i%p[j]==0){
				mu[k]=0;
				mx[k]=mx[i]+1;
				sum[k]=sum[i]/mx[i]*mx[k];
				break;
			}
			mu[k]=-mu[i];
			mx[k]=2;
			sum[k]=sum[i]*2;
		}
	}
	for(int i=1;i<=N;i++) mu[i]+=mu[i-1],sum[i]+=sum[i-1];
}
int main()
{
	Prime(maxn-5);
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d%d",&n,&m);if(n>m) swap(n,m);
		long long ans=0;
		for(int i=1,j;i<=n;i=j+1)
		{
			j=min(n/(n/i),m/(m/i));
			ans+=1ll*sum[n/i]*sum[m/i]*(mu[j]-mu[i-1]);
		}
		printf("%lld\n",ans);
	}
}