1、 情景分析

 
$\qquad$Alice想與Bob安排晚餐，由於他們都不願意使用手機的“通話”功能，她傳送簡訊建議在晚上6點見面。但是，發簡訊是不可靠的，Alice無法確定Bob的手機是否接受到了該訊息。如果她收到來自Bob的確認訊息，將會前往會面點。但Bob不能保證Alice收到了他的確認資訊；如果確認資訊丟失，Alice無法確定Bob是否收到她的建議，或者Bob的確認訊息是否丟失。因此，Bob要求Alice發出一條確認訊息，以確保她會在那裡。但是這條訊息也會丟失…
可以看到，如果Alice和Bob都想確定對方會來到會面點，這樣的訊息交換將永遠持續下去。
Remark：

• 此類協議無法終止：假設存在很多需要達成共識的協議，且P是需要最少數量訊息的協議之一。由於最後的確認訊息可能會丟失，並且協議仍需要確認協議，我們可以簡單地決定始終省略最後一條訊息。這給了我們一個新的協議P0，它需要的訊息少於P，與P需要最少量訊息的假設相矛盾。
• Alice和Bob可以使用Paxos嗎？
  答：不可以，如果兩個人都向伺服器申請最新票號，各佔據1/2的伺服器，都不放棄資源，互相僵住。

2、共識

 
$\qquad$

• 一致性 所有正確的節點決定相同的值。
• 終止 所有正確的節點在有限時間內終止。
• 有效性 決策值必須是節點的輸入值。

Remark：

• 非同步模型（asynchronous model）的主要特點是：
  1.程序之間的通訊基於訊息（message）。訊息的傳輸是可靠的，即訊息可能延遲，可能亂序，但最終都會到達。
  2.沒有時鐘（clock）可用，因此程序無法做出訊息超時的判斷。
  3.程序的存活狀態是無法檢測的，即外部不能區分程序執行緩慢或是終止的情況；但是程序的執行是“誠實”的，沒有“Byzantine Failures”。

• 我們假設每個節點都可以向每個其他節點發送訊息，並且連線可靠，訊息發出去會被接收。

• 沒有廣播媒體。如果節點想要向多個節點發送訊息，則需要傳送多個單獨的訊息。

• Paxos是否同時滿足三個標準？
  實際上，Paxos不保證終止。例如，如果兩個客戶端連續請求票證，系統可能永遠停留，並且他們都沒有辦法獲得多數票。

3、不可能達成共識

3.1 FLP理論
$\qquad$在非同步通訊場景，分散式系統中只要有一個程序/節點不可用（失去響應或暫停），沒有任何確定性演算法能保證可用程序/節點能達成共識。（No completely asynchronous consensus protocol can tolerate even a single unannounced process death）
$\qquad$ 來源於Fischer、Lynch和Patterson三位科學家於1985年發表的論文《Impossibility of Distributed Consensus with One Faulty Process》。FLP Impossibility（FLP不可能性）是分散式領域中一個非常著名的結果，該結果在專業領域被稱為“定理”，其地位之高可見一斑。該結果在2001年無懸念地被授予PODC影響力論文獎（現稱為 Dijkstra獎）。
$\qquad$在理論情況下（嚴格滿足一致性agreement、終止性/無鎖termination、合法性/有效性validity），結果是impossible。
$\qquad$實際場景中，三個要求需要有所取捨（可參見CAP理論），或者使用隨機演算法而不使用確定性演算法。

3.2 相關概念
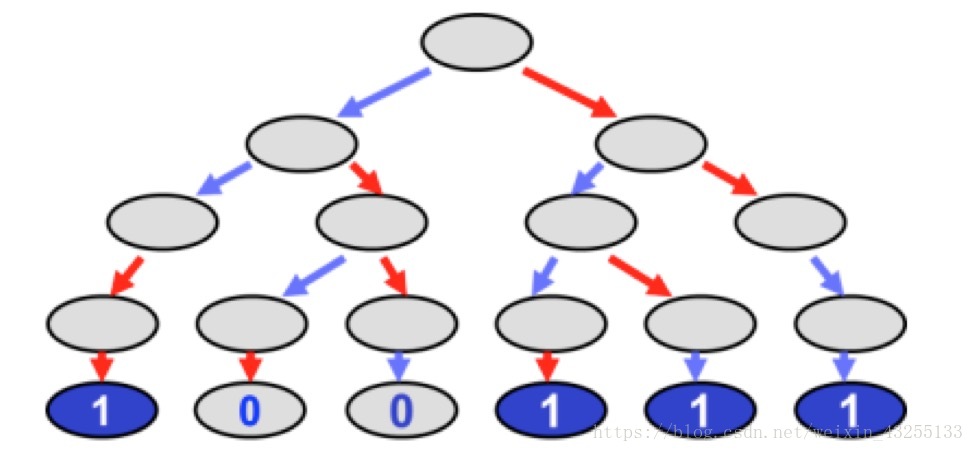
$\qquad$ 狀態樹、單可能的（確定的）、雙可能的/不確定的、1價等概念如下圖所示。
$\qquad$注意：注意由於訊息沒有先後順序，導致狀態樹的結構非常龐大，而圖中只是實際狀態樹的簡化版本。作者在證明定理時也沒有描繪出完整的狀態樹，只是利用特殊節點找到最壞的可能從而找到了矛盾。



$\qquad$定義3.1 狀態（configuration）：我們說系統是由其狀態C完全定義的（在執行期間的任何時刻）。狀態包括每個節點的值，以及正在傳輸（已傳送但尚未接收）的所有訊息。
$\qquad$注意：狀態包含兩部分，節點的值和正在傳輸的訊息。
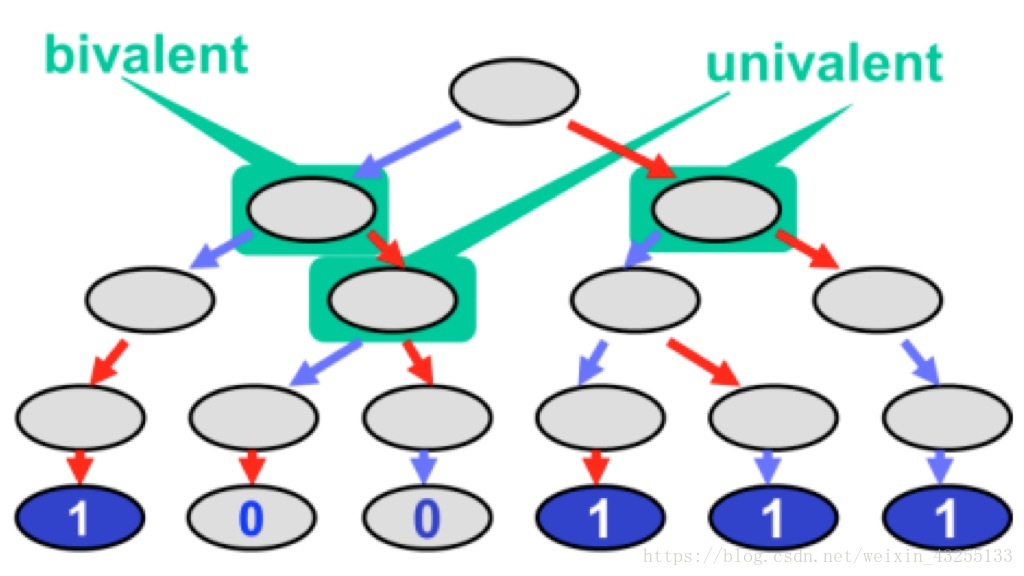
$\qquad$定義3.2 單可能的/確定的：如果確定決策值與之後發生的事情無關，則我們將配置C稱為單可能的/確定的。
$\qquad$定義3.3 雙可能的/不確定的：如果節點可能決定為0或1，則配置C稱為雙可能的/不確定的。
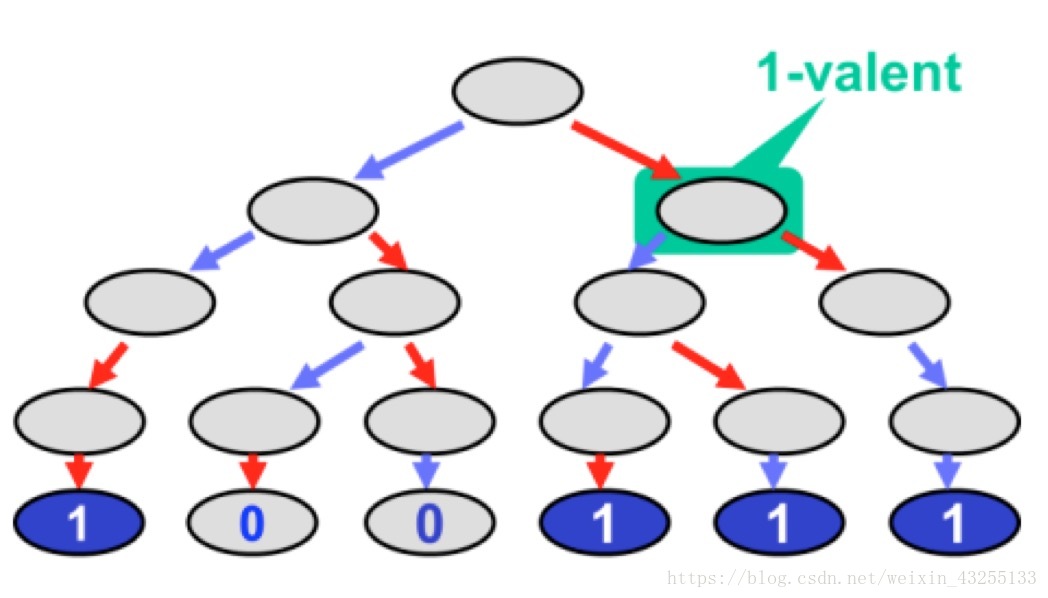
$\qquad$注意：注意雙可能的/不確定的包含兩種情況（0價和1價），0價的子節點全是0價，最終決定0；1價的子節點全是1價，最終決定1。
$\qquad$定義3.4 傳輸：從狀態C到後續狀態Cτ的轉換由事件τ=（u; m）表徵，即節點u接收訊息m。
$\qquad$注意：當m被u接收到時，C轉換為Cτ。
$\qquad$定義3.5（狀態樹） 狀態樹是狀態的有向樹。 其根是狀態C0，其完全由輸入值V表徵。 樹的邊緣是傳輸; 每個狀態都具有所有適用的傳輸作為傳出邊。

3.3 證明過程
$\qquad$定理用反正法進行證明，先假設存在一個共識演算法，通過找出矛盾來證明共識演算法不存在。
$\qquad$定理只證明了二分輸入（輸入只能是0或1）的情況下，共識演算法不存在。因為二分輸入對於共識演算法的最簡單的情況，所以在更多輸入的情況下，共識演算法更不可能存在。
$\qquad$證明中首先關注初始狀態：
$\qquad$引理3.7 如果f≥1，則存在至少一種輸入值V的選擇，使得相應的初始狀態C0是不定的。
$\qquad$上面的引理將關注點放到了初始狀態C為二價/不定的情況，注意f指的是不可用節點的數量。
$\qquad$下面插入一條引理來說明對於任意C，u1≠u2時，Cτ1τ2=Cτ2τ1。
$\qquad$引理3.10 假設u1≠u2的兩個傳輸τ1=（u1; m1）和τ2=（u2; m2）都適用於C.令Cτ1τ2是通過首先應用轉變τ1然後τ2而遵循C的狀態，並且讓Cτ2τ1為類似地定義。 它認為Cτ1τ2=Cτ2τ1。
$\qquad$下面的定理關注到了臨界狀態：
$\qquad$引理3.12 如果系統處於不定狀態，它必須在有限時間內達到臨界狀態，或者它不能解決共識。
$\qquad$將3.7與3.12連在一起理解可得出結論：臨界狀態一定存在。
$\qquad$引理3.13 如果狀態樹包含臨界狀態，則崩潰單個節點可以建立不定葉節點; 即，崩潰阻止演算法達成一致。
$\qquad$3.13的解釋：對於臨界節點來說，存在價不相同的Cτ1和Cτ2 ，這會使Cτ1τ2=Cτ2τ1不成立，從而使u1=u2，可證臨界狀態中的所有訊息都被同一節點接受，如果該節點失效，則演算法無法繼續進行，也就無法達成共識。
前面的引理證明了臨界狀態一定存在，而3.13證明了臨界狀態會導致達不成共識。所以將這些引理組合起來就得到了FLP定理：
$\qquad$定理3.14 f> 0時，沒有確定性演算法總是在非同步模型中達成共識。

4、 隨機共識演算法

 
$\qquad$由FLP可知，在網路可靠的前提下，任意節點失效，非同步系統中不存在一個解決一致性問題的確定性演算法，因此本節介紹了一個簡單的解決一致性問題的隨機性演算法。
$\qquad$演算法如下：

Algorithm 3.15 Randomized Consensus (Ben-Or)
1：vi ∈{0,1} ▹inputbit
2:  round = 1
3:  decided = false
4:  Broadcast myValue(vi, round)//廣播自己的值
5:  while true do
      Propose
6:  Wait until a majority of myValue messages of current round arrived //等待接收到大於等於n/2個節點數的資訊
7:  if all messages contain the same value v then
8:  Broadcast propose(v, round)//廣播目的
9:  else
10: Broadcast propose(⊥, round)//廣播空
11: end if
12: if decided then
13: Broadcast myValue(vi, round+1)//廣播自己的值
14: Decide for vi and terminate//該節點達成共識
15: end if
     Adapt
16: Wait until a majority of propose messages of current round arrived////等待接收到大於等於n/2個節點數的資訊
17: if all messages propose the same value v then
18: vi = v
19: decide = true
20: else if there is at least one proposal for v then
21: vi = v
22: else
//隨機選擇自己的值
23: Choose vi randomly, with Pr[vi = 0] = Pr[vi = 1] = 1/2
24: end if
25: round = round + 1
26: Broadcast myValue(vi, round)
27: end while 

我們來舉幾個簡單例子
$\qquad$例子中0代表今天不吃飯，1代表今天吃飯，多人協商今天是否吃飯問題。

$\qquad$例1．有三個節點，在通訊過程時都正常無崩潰的執行。三個節點A、B、C的輸入分別為0、1、1。因此C0為（011）。
$\qquad$第一輪：
$\qquad$ - 對於A來說Broadcast myValue(0, 1) 隨後Broadcast propose（1，1），然後執行第23行，隨機選取自己的值，可能為1，或為0。若為1則達成一致，若為0，Broadcast myValue(0, 2) ，重複第一輪步驟，直到隨機成1。
$\qquad$ - 對於B來說Broadcast myValue(1, 1) 隨後Broadcast propose（⊥ ，1），然後執行第21行，把自己的值改變成1，隨後Broadcast myValue(1, 2) 。
$\qquad$ - 對於C來說Broadcast myValue(1, 1) 隨後Broadcast propose（⊥ ，1），然後執行第21行，把自己的值改變成1，隨後Broadcast myValue(1, 2)。

$\qquad$例2: 有四個節點，A、B、C、D輸入分別為0、0、1、1。因此C0為（0011）
$\qquad$第一輪：
$\qquad$ - 對於A來說Broadcast myValue(0, 1) 隨後Broadcast propose（⊥，1），然後執行第23行，隨機選取自己的值，可能為1，或為0。
$\qquad$ - 對於B來說Broadcast myValue(0, 1) 隨後Broadcast propose（⊥ ，1），然後執行第23行，隨機選取自己的值，可能為1，或為0。
$\qquad$ - 對於C來說Broadcast myValue(1, 1) 隨後Broadcast propose（⊥ ，1），然後執行第23行，隨機選取自己的值，可能為1，或為0。
$\qquad$ - 對於C來說Broadcast myValue(1, 1) 隨後Broadcast propose（⊥ ，1），然後執行第23行，隨機選取自己的值，可能為1，或為0。

$\qquad$ 可以看出演算法的時間複雜度為 $O（2^n）$，即最壞情況下。

注意：
$\qquad$ 1. 演算法中第6行和第16行，需要接收到大於等於2/n的節點訊息，才能正常執行下面的步驟。
$\qquad$ 2. 該演算法最多能容忍f<n/2的節點崩潰。

$\qquad$ 定義3.16 只要節點集沒有達成共識，即使有節點崩潰演算法3.15也總會有所進展，

$\qquad$ 定義3.17 演算法3.15滿足共識中的有效性要求。

$\qquad$定義3.18 演算法3.15滿足共識中的一致性要求。

$\qquad$ 定理3.19 演算法3.15滿足共識中的終止要求，所有節點在 $O（2^n）$時間之內終止。

$\qquad$ 定理3.20 當崩潰節點f>=n/2時，在非同步模型中沒有共識演算法能達成一致。

5、分享硬幣

 
$\qquad$該演算法用來改進3.15演算法中第23行，加快達成共識的速度。

Algorithm 3.22 Shared Coin (code for node u)
//對於節點U ，硬幣cu 以1/n的概率取0，以1-n/n的概率取1
1: Choose local coin cu = 0 with probability 1/n, else cu = 1
//節點U向所有節點廣播自己的硬幣cu
2: Broadcast myCoin(cu)
//等待至少n-f個節點的硬幣取值，並將所有取值儲存下來形成硬幣集Cu
3: Wait for n − f coins and store them in the local coin set Cu
//節點U廣播自己的硬幣集
4: Broadcast mySet(Cu)
//等待至少n-f個節點的硬幣集Cu
5: Wait for n − f coin sets
//如果在所有硬幣集中某個硬幣集存在一個硬幣取值0，那麼u節點便取輸入值為0
6: if at least one coin is 0 among all coins in the coin sets then
7:     return 0
8: else
//否則取1
9:     return 1
10: end if

$\qquad$定義 3.23. u是一個節點，假設W是u從至少f+1個不同的硬幣集裡接收到的硬幣集，那麼W中至少包含f+1個不同的節點取值。

$\qquad$定義 3.24. 在W中所有的硬幣取值都可以被所有正常執行的節點觀察到

$\qquad$定義 3.25. 分享硬幣演算法3.22最多可以容忍(n/3)-1個節點崩潰

$\qquad$定義 3.26. 把演算法3.22插入到演算法3.15中，我們將可以獲得一個可以在常數輪期望時間內終止，並且最多容忍(n/3)-1個節點崩潰的隨機共識演算法。