資料庫基礎(2)選擇,投影,連線,除法運算
關係資料庫中的選擇,投影,連線,除法都是很重要的運算
選擇
定義:在關係中選擇在指定屬性上有確定值的關係的子集。表示為:

選擇運算是選擇關係中行的子集,即選擇滿足條件的元組
例:
1.查詢資訊系(IS系)全體學生
σ Sdept=‘IS’(Student)
2.查詢年齡小於20歲的學生
σ Sage<20(Student)
選擇運算的特性:

投影
投影是選取關係中列的子集。設模式R上關係r,X是R上屬性的子集(x就是列),r到 X上的投影r`表示為:
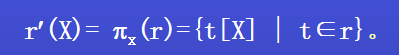
投影操作是從列的角度進行行的運算。投影的結果不是原來的關係,是X中的幾列屬性。
特別注意
投影結果中不應該包含重複行
例子:查詢學生關係Student中都有哪些系,即查詢關係Student上所在系屬性上的投影
Student關係如圖所示:
| Sname | Sdept |
|---|---|
| 李勇 | CS |
| 劉晨 | CS |
| 王小明 | MA |
| 張超 | IS |
求 : π Sdept(Student)
因為Student關係原來有4個元組,但是我們的投影結果需要取消重複的CS元組,因此投影結果只有三個元組:
| Sdept |
|---|
| CS |
| MA |
| IS |
投影的特性

連線(Join):自然連線,等值連線
定義: 連線也稱為θ連線。它是從兩個關係的笛卡爾積中選取屬性間滿足一定條件的元組。
記作:
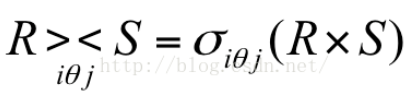
(θ為比較符: >,<,≥,≤,=,≠)
1.等值連線
θ為 = 符號的連線運算稱為等值連線。它是從關係R與S的廣義笛卡爾積中選取A , B 屬性值相等的那些元組。

(被水印遮住的地方是A=B)
2.自然連線
自然連線是一種特殊的等值連線。它要求兩個關係中進行比較的分量必須是同名的屬性組,並且在結果中把重複的屬性列去掉
表示為: R⋈S={t r⌒ts |tr∈R∧ts∈S∧tr[B]=ts[B]}
(自然連線也可看作是在廣義笛卡爾積R×S中選出同名屬性上符合相等條件元組,再進行投影,去掉重複的同名屬性,組成新的關係。)
所以等值連線和自然連線的區別是
自然連線是去除了重複的屬性列的!
例題
求R和S的自然連線,等值連線,以及非等值連線R[C<E]S 的結果
R :
| A | B | C |
|---|---|---|
| a1 | b1 | 5 |
| a1 | b2 | 6 |
| a2 | b3 | 8 |
| a2 | b4 | 12 |
S:
| B | E |
|---|---|
| b1 | 3 |
| b2 | 7 |
| b3 | 10 |
| b3 | 2 |
| b5 | 2 |
自然連線:R⋈S
| A | B | C | E |
|---|---|---|---|
| a1 | b1 | 5 | 3 |
| a1 | b2 | 6 | 7 |
| a2 | b3 | 8 | 10 |
| a2 | b3 | 8 | 2 |
等值連線:R[R.B=S.B]S
| A | R.B | C | S.B | E |
|---|---|---|---|---|
| a1 | b1 | 5 | b1 | 3 |
| a1 | b2 | 6 | b2 | 7 |
| a2 | b3 | 8 | b3 | 10 |
| a2 | b3 | 8 | b3 | 2 |
非等值連線:R[C<E]S
| A | R.B | C | S.B | E |
|---|---|---|---|---|
| a1 | b1 | 5 | b2 | 7 |
| a1 | b1 | 5 | b3 | 10 |
| a1 | b2 | 6 | b2 | 7 |
| a1 | b2 | 6 | b3 | 10 |
| a2 | b3 | 8 | b3 | 10 |
除法運算(division)
設關係R除以關係S的結果為關係T,則T包含所有在R但不在S中的屬性及其值,且T的元組與S的元組的所有組合都在R中
除法的結果可以用計算象集的方法來解決,以一道題為例來說明怎麼求除法
例題:已知關係R和S如下,求R➗S的結果

第一步 : 因為R÷S所得到的屬性值 是包含於R,但是S不包含的屬性, 所以R➗S得到的屬性列有(A,B),S在(C,D)屬性上的投影為{(c1,d1),(c2,d2)}
第二步 : 關係R中,AB屬性可以取值為={(a1,b1),(a2,b2),(a3,b3)}
第三步 : 求象集
- (a1,b1)={(c1,d1),(c2,d2),(c3,d3)}
- (a2,b2)={(c2,d2)}
- (a3,b3)={(c1,d1),(c2,d2)}
第四步: 從第三步中可以發現,有象集(a1,b1)和(a3,b3)包含了S在(C,D)屬性上的投影,所以R÷S={(a1,b1),(a3,b3)}
| A | B |
|---|---|
| a1 | b1 |
| a3 | b3 |
