關係的布林運算主要包括：並，交，差，廣義笛卡爾積，補，有效補

並集

定義： 關係R和S的並集結果，由屬於R或屬於S的所有元組組成，其結果是一個新關係。記為：

Q = R ∪ S = {t | t ∈ R 或 t ∈ S }

例子： 注意！ 這個並集求出來是不含重複元組的！例如雖然R和S都含有(a1,b2,c2)，但是合併的結果中，只出現一次(a1,b2,c2)

差集

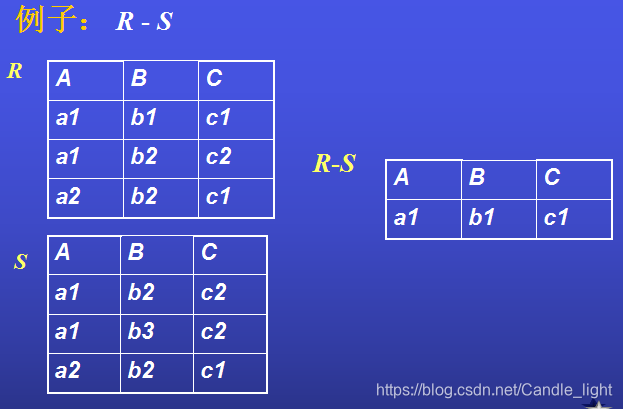
定義： 關係R和S的差由屬於R但不屬於S的所有元組組成。記為：
Q = R - S = {t | t ∈ R 但 t ∉ S }
例子

交集

定義： 關係R和S的交集結果由既屬於R又屬於S的所有元組組成。記為：
Q = R ⌒ S = {t | t ∈ R 且 t ∈ S }

廣義笛卡爾積

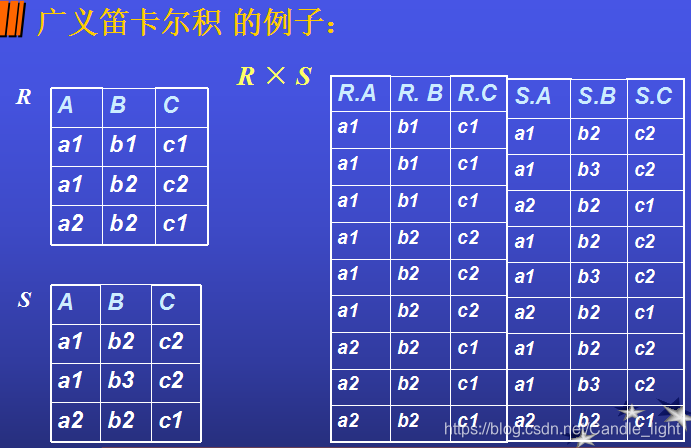
關係R和關係S的笛卡爾積為R中所有元組和S中所有元組的串接。
結果關係的屬性個數：k1+k2 （k1和k2分別為關係S的屬性數）
結果關係的元組數： m x n （m和n分別為R和S的元組數）
例子：

補集和有效補集

1.首先看看補集定義：

關係模式R(A1,A2,…,An)， R上的關係r。
補運算：設dom( R )表示模式R上的所有元組的集合，則關係r的補為：
r的補集 = dom( R )－r
我們可以按照數學裡的補集來理解，其實就是 (集合r + r的補集 = 全集) ，只不過這裡的全集是關係R上的所有元組的集合
例題：

這道題，我們首先要知道關係R上的全集（全部元組）是什麼，然後用全集減去r，就可以得到r的補集了
R上的全集是A和B的廣義笛卡爾積，即：
R=（A，B）={(a1,b1),(a1,b2),(a2,b1),(a2,b2),(a3,b1),(a3,b2)}
所以用R中的元組減去r 即可得到r補集

2.有效補集

有效補集的定義看上去太麻煩，我們這裡直接以一道題來講怎麼求有效補

第一步 求出R： R=（A，B）={(a1,b1),(a1,b2),(a2,b1),(a2,b2),(a3,b1),(a3,b2)}

第二步 理解有效值域。關係r的有效值域是指，關係r中各個屬性的取值範圍。比如說我們這道題裡面的r ，它的屬性A的屬性取值範圍是（a1,a2），屬性B的取值範圍是（b1,b2），所以r元組的有效值域就是(A,B)=｛A ∈ (a1,a2) 且 B ∈ (b1,b2)｝。 因此我們求有效補集的全集就不再是R，而是R*，R* 中屬性的值域就是r的有效值域。

第三步

有效補的應用：當關系元組數比其有效補元組數多得多時，有效補可作為資料壓縮手段。
例如：學生選課，一個班有50個學生選資料庫課，3個學生不選， 則儲存選修了資料庫課的學生可用儲存其有效補實現。

最後再來做一道例題吧

（1）求補集
首先計算R，即A,B,C的笛卡爾積，R= A x B x C = ｛（a1,b1,c1）,(a1,b1,c2),(a1,b2,c1),(a1,b2,c2),(a1,b3,c1),(a1,b3,c2),(a2,b1,c1),(a2,b1,c2),(a2,b2,c1),(a2,b2,c2),(a2,b3,c1),(a2,b3,c2)｝
所以r的補集=R-r = {(a1,b1,c2),(a1,b2,c1),(a1,b2,c2),(a1,b3,c1),(a1,b3,c2),(a2,b1,c2),(a2,b2,c2),(a2,b3,c2)}
（2）求有效補
首先確定r的有效值域： r中屬性A的範圍是（a1,a2），屬性B的範圍是（b1,b2,b3），屬性C的範圍是（c1）
所以可以得到R*={（a1,b1,c1）,(a1,b2,c1),(a1,b3,c1),(a2,b1,c1),(a2,b2,c1),(a2,b3,c1)}
因此r的有效補集=R*-r = {(a1,b2,c1),(a1,b3,c1)}