逃生

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 7786    Accepted Submission(s): 2274

 

Problem Description

糟糕的事情發生啦，現在大家都忙著逃命。但是逃命的通道很窄，大家只能排成一行。

現在有n個人，從1標號到n。同時有一些奇怪的約束條件，每個都形如：a必須在b之前。
同時，社會是不平等的，這些人有的窮有的富。1號最富，2號第二富，以此類推。有錢人就賄賂負責人，所以他們有一些好處。

負責人現在可以安排大家排隊的順序，由於收了好處，所以他要讓1號儘量靠前，如果此時還有多種情況，就再讓2號儘量靠前，如果還有多種情況，就讓3號儘量靠前，以此類推。

那麼你就要安排大家的順序。我們保證一定有解。

 

Input

第一行一個整數T(1 <= T <= 5),表示測試資料的個數。
然後對於每個測試資料，第一行有兩個整數n(1 <= n <= 30000)和m(1 <= m <= 100000)，分別表示人數和約束的個數。
然後m行，每行兩個整數a和b，表示有一個約束a號必須在b號之前。a和b必然不同。

 

Output

對每個測試資料，輸出一行排隊的順序，用空格隔開。

 

Sample Input

1
5 10
3 5
1 4
2 5
1 2
3 4
1 4
2 3
1 5
3 5
1 2

Sample Output

1 2 3 4 5

Author

CLJ

Source

BestCoder Round #1

【分析】一開始直接用拓撲排序+優先佇列做的，然後就wa了幾發。搜了下題解，發現要用反向拓撲...反正我大概率想不到的啦

貼一份別人家的思路！

原文連結

【題意】

• 有n個人，m個優先順序a，b
• 表示a優先於b，並且每個人有個編號的優先順序，輸出順序。

【分析】

• 編號最小的節點要儘量排在前面；在滿足上一個條件的基礎上，編號第二小的節點要儘量排在前面；在滿足前兩個條件的基礎上，編號第三小的節點要儘量排在前面……依此類推。（注意，這和字典序是兩回事，不可以混淆
  。）
• 不是字典序，自然不能每次優先佇列優先最小編號出隊。
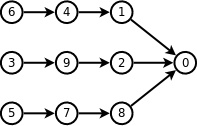
• 這裡有個例子，有三條互相平行的路徑：6 → 4 → 1、 3 → 9 → 2 和 5 → 7 → 8。一條路徑上的各個節點的先後關係都是不能改變的。

• 如果直接優先佇列優先最小值的話去求的結果會是：3 5 6 4 1 7 8 9 2 0
• 是不符合題意要求的，因為明顯可以使1號點排在更前邊。
• 正確的順序應該是6 4 1 3 9 2 5 7 8 0
• 那麼我們如何去求這個結果呢，使用反向拓撲 + 優先佇列（優先最大值），壓入的時候反向壓進。
• 這樣想，我們每次優先最小的並不能保證按上述的順序排列，但是，我們優先最大值，把編號大的點給他分配一個儘量大的一個編號，這肯定是符合要求的，最後倒序輸出即可。

【程式碼】

#include<bits/stdc++.h>
using namespace std;

const int maxn=3e4+5;
vector<int>G[maxn];
int in[maxn];
bool vis[maxn];

int n,m;

int main()
{
	int T;scanf("%d",&T);
	while(T--)
	{
		memset(vis,false,sizeof(vis));
		memset(in,0,sizeof(in));
		for(int i=0;i<=n;i++)G[i].clear();
		scanf("%d%d",&n,&m);
		for(int i=1;i<=m;i++)
		{
			int a,b;
			scanf("%d%d",&a,&b);
			vis[a]=1;vis[b]=1;
			G[b].push_back(a);
			in[a]++;
		}
		int num=0;
		priority_queue<int>pq;
		for(int i=1;i<=n;i++)
			if(in[i]==0)pq.push(i);
		vector<int>ans;
		while(!pq.empty())
		{
			int u=pq.top();
			ans.push_back(u);
			pq.pop();
			for(int i=0;i<G[u].size();i++)
			{
				int v=G[u][i];
				if(--in[v]==0 && vis[v])pq.push(v);
			}
		}
		for(int i=ans.size()-1;i>=0;i--)
		{
			if(i)printf("%d ",ans[i]);
			else printf("%d\n",ans[i]);
		}
	}
	return 0;
}