機器學習尤其針對分類器這，有各種指標來評判最終的模型效果，以前總聽說混淆矩陣，也不知道到底幹啥的，反正聽著就讓人很混淆，後來看了網上兩篇文章，自己又實踐一下，基本搞明白了，我給它起了個新名字，叫“分類結果統計矩陣“，非TM拽那麼高大上的名字幹啥，聽著都讓人望而卻步了，還有一些機器學習必備裝B名詞，梯度爆炸、深度神經網路、反向傳播，都是裝B名詞，其實只有明白人才知道都是前輩們幾十年前搞爛的東西，唉，通俗點不好麼？？？

下面我把這兩篇文章轉載過來，地址都放在了每篇文章的後面了。

1、在機器學習領域，混淆矩陣（confusion matrix），又稱為可能性表格或是錯誤矩陣。它是一種特定的矩陣用來呈現演算法效能的視覺化效果，通常是監督學習（非監督學習，通常用匹配矩陣：matching matrix）。其每一列代表預測值，每一行代表的是實際的類別。這個名字來源於它可以非常容易的表明多個類別是否有混淆（也就是一個class被預測成另一個class）。

假設有一個用來對貓（cats）、狗（dogs）、兔子（rabbits）進行分類的系統，混淆矩陣就是為了進一步分析效能而對該演算法測試結果做出的總結。假設總共有 27 只動物：8只貓， 6條狗， 13只兔子。結果的混淆矩陣如下圖：

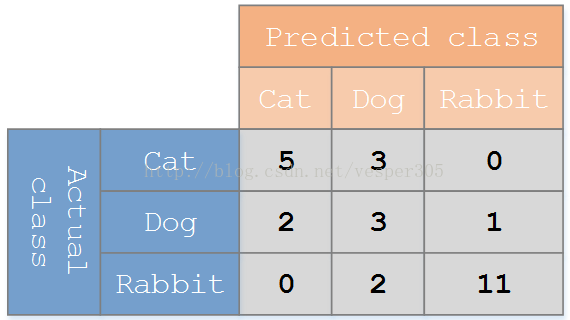
在這個混淆矩陣中，實際有 8只貓，但是系統將其中3只預測成了狗；對於 6條狗，其中有 1條被預測成了兔子，2條被預測成了貓。從混淆矩陣中我們可以看出系統對於區分貓和狗存在一些問題，但是區分兔子和其他動物的效果還是不錯的。所有正確的預測結果都在對角線上，所以從混淆矩陣中可以很方便直觀的看出哪裡有錯誤，因為他們呈現在對角線外面。

在預測分析中，混淆表格（有時候也稱為混淆矩陣），是由false positives，falsenegatives，true positives和true negatives組成的兩行兩列的表格。它允許我們做出更多的分析，而不僅僅是侷限在正確率。準確率對於分類器的效能分析來說，並不是一個很好地衡量指標，因為如果資料集不平衡（每一類的資料樣本數量相差太大），很可能會出現誤導性的結果。例如，如果在一個數據集中有95只貓，但是隻有5條狗，那麼某些分類器很可能偏向於將所有的樣本預測成貓。整體準確率為95%，但是實際上該分類器對貓的識別率是100%，而對狗的識別率是0%。

對於上面的混淆矩陣，其對應的對貓這個類別的混淆表格如下：

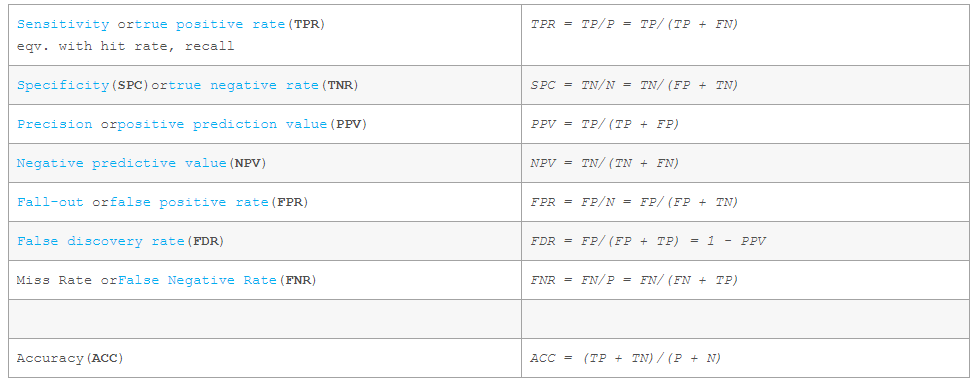
假定一個實驗有 P個positive例項，在某些條件下有 N 個negative例項。那麼上面這四個輸出可以用下面的偶然性表格（或混淆矩陣）來表示：

公式定義如下：

轉載自https://blog.csdn.net/vesper305/article/details/44927047

2、我理解上的混淆矩陣就是一個分類器對於正反例（假設是二分類，多分類也類似）的混淆程度。

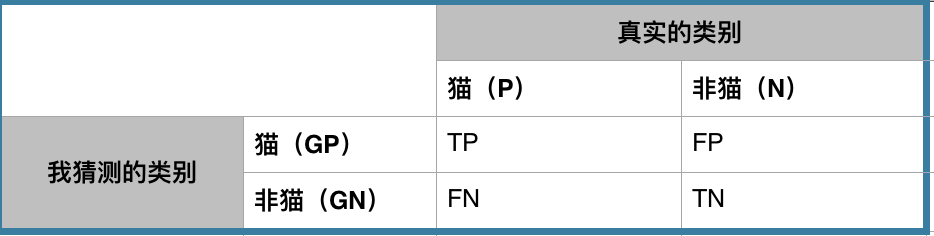
我有見過兩種不同混淆矩陣，主要區別是對於真實的類別和猜測的類別的位置互換。其實本質上沒有大區別的，看每一個人的習慣。這裡採用wikipedia的格式。

初學者一般看到這個矩陣的描述就暈了。怎麼那麼多字母？TP，FP，FN，TN是什麼？就算告訴你TP=True Positive的意思，你也要暈半天，更別說之後的各種度量公式。如PPV， NPV，Recall， F1，ROC等等。

怎麼生成混淆矩陣
假設測試資料中我有5個貓圖片和8個非貓圖片的例子。首先在貓(P)的地方的P填寫5， 非貓(N)的地方的N填寫8。說明測試資料中真實的類別貓有5例，非貓有8例。

在TP，FP，FN，TN的地方都填上0。

接下去從13例測試例子中一例一例的問分類器（也就是我），比如拿一例貓圖片問我，我回答是貓，那麼在TP的地方就加1。如果我回答了非貓，那麼在FN的地方就加1。再比如拿一例非貓的圖片問我，我回答是非貓，那麼在TN的地方加1，如果我回答了貓，那麼在FP的地方加1。

等13例都問完之後，那麼整個混淆矩陣也就完成了。如下圖：

基本用語的解釋
condition positive (P) = 測試資料中正例的數量。此處是貓=5。
condition negatives (N) = 測試資料中反例的數量。此處是非貓=8。
true positive (TP) = 是正例，且很幸運我也猜它是正例的數量。此處4表示有4張圖片是貓，且我也猜它是貓。TP越大越好，因為表示我猜對了。這個時候如果你質問我貓不是5張圖片嗎？那麼別急，重新看看TP的定義。然後再看看FN的定義。
false negtive (FN) = 明明是正例，但很不幸，我猜它是反例的數量。此處1表示有1張圖片明明是貓，但我猜它非貓。FN越小越好，因為FN說明我猜錯了。現在來看5張貓圖片是不是全了。其中4張貓我猜是貓，1張貓我猜非貓。
true negative (TN) = 是反例，且很幸運我也猜它是反例的數量。此處5表示有5張圖片是非貓，且我也猜它是非貓。TN越大越好，因為表示我猜對了。
false positive (FP) = 明明是反例，但很不幸我猜它是正例的數量。此處3表示有3張圖片是非貓，但我猜它是貓。FP越小越好，因為FP說明我猜錯了。

小總結：
正對角線的數字越大越好，因為都是我猜對的次數。
其他地方越小越好，因為都是我猜錯的次數。
豎的列加起來就是測試資料中貓和非貓的各自真實的資料量。
橫的行加起來就是我猜貓和我猜非貓的次數。
補充：GP的意思就是I guess positive，注意GP是我自己定的，不是官方標準。GN就是I guess negtive。

各種度量
這裡開始才是重點，可能要配合一定的實踐，才能更加深刻的領悟其中的奧妙。

sensitivity, recall, hit rate, or true positive rate (TPR)
以上的幾種說法都是一個意思。硬翻譯的話是靈敏度，召回度，命中率或者是正例中猜對的比例。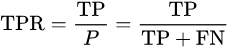

* 理解1：範圍是0-1， 貓的例子中sensitivity=4/5=0.8
* 理解2： 分母是真實正例的總數，和你的猜測值無關
* 理解3： 分子是你猜正例且猜對的次數，和其他都無關。反例你猜對的再多和分子沒有關係。
* 理解4： 如果對於所有的測試資料，你都猜是正例，則該值肯定是1。假設貓的例子，你如果13張圖片都猜是貓，那麼你的TRP = 5／5 = 1。由於測試資料中存在非貓，所以你對於貓過於靈敏，這大概也是為什麼sensitivity的命名原因。recall（召回）的原因是總共有5只貓，你把5只貓都找對了，所以叫做召回了所有的貓。
* 理解5： 該值越大，表示分類器對正例越靈敏，越能找全所有的正例。
* 理解6： 好的分類器該值要大，僅該值大的分類器不一定就好。單獨該值無法判斷分類器的優劣。因為好的分類器不但要對正例靈敏，還要對反例專一。

specificity or true negative rate (TNR)
以上兩種說法也是一個意思。specificity翻譯過來是特異度，專一度。我理解是靈敏度的反義詞。就是不要看到任何例子都猜是正例，要有自己的見解和專一。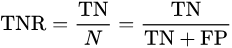

* 理解1：範圍是0-1， 貓的例子中specificity=5/8=0.625
* 理解2： 分母是真實反例的總數，和你的猜測值無關
* 理解3： 分子是你猜反例且猜對的次數，和其他都無關。正例你猜對的再多和分子沒有關係。
* 理解4： 如果對於所有的測試資料，你都猜是反例，則該值肯定是1。假設貓的例子，你如果13張圖片都猜是非貓，那麼你的TNR = 8／8 = 1。由於測試資料中存在貓，所以你對於非貓過於專一，這大概也是為什麼specificity的命名原因。
* 理解5： 該值越大，表示分類器對反例越專一。
* 理解6： 好的分類器該值要大，僅該值大的分類器不一定就好。單獨該值無法判斷分類器的優劣。因為好的分類器不但要對反例專一，還要對正例靈敏。

precision or positive predictive value (PPV)

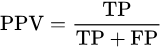
PPV也就是正例的precision。
大家經常會看到precision和recall經常出現，因為precision和recall的綜合表現，可以基本揭示分類器對於正例的好壞程度。

理解1： 整個的意思就是你總共猜了幾次是貓（分母），其中猜對多少次（分子）。貓的例子中PPV = 4/7 = 0.57。
理解2： 如果分類器比較保守，它只對最有把握的一張圖片說是貓（假設這種確實是貓），而說其他都不是貓。那麼它的precision就是100%。想想公式，你總共猜了幾次是貓是分母，其中猜對了多少次是分子。
理解3：13張圖片中總共5只是貓，如果你為了找全貓，從而猜說13張都是貓，那麼你的recall（召回率）或者sencitivity（敏感度）會非常高，等於1。但是犧牲的是precision，因為你猜了13次貓會作為分母，而猜對的5次是分子，所以precision = 5/13 = 0.38。（叫你瞎猜！）
理解4： 一般分類器猜正例比較激進，那麼recall會比較好看，但是precision會比較難看，如果分類器猜正例比較保守，那麼precision會比較高，但是recall就不一定高。

negative predictive value (NPV)

NPV完全就是和PPV相對的東西了。PPV是分類器猜正例的正確率，NPV是分類器猜反例的正確率。

理解1：整個的意思就是你總共猜了幾次是非貓（分母），其中猜對多少次（分子）。貓的例子中NPV = 5/6 = 0.83。
理解2：PPV + NPV 不等於1。想想極端例子，13張圖我全猜貓，PPV=1，NPV=0/0沒有意義。你都不猜反例，讓我怎麼評價你的猜反例的正確率。

accuracy (ACC)

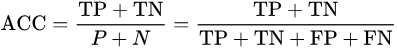
整體的正確率。即猜對的次數（無論是正例還是反例）除以總測試資料的總數。

看幾個混淆矩陣

完美的分類器

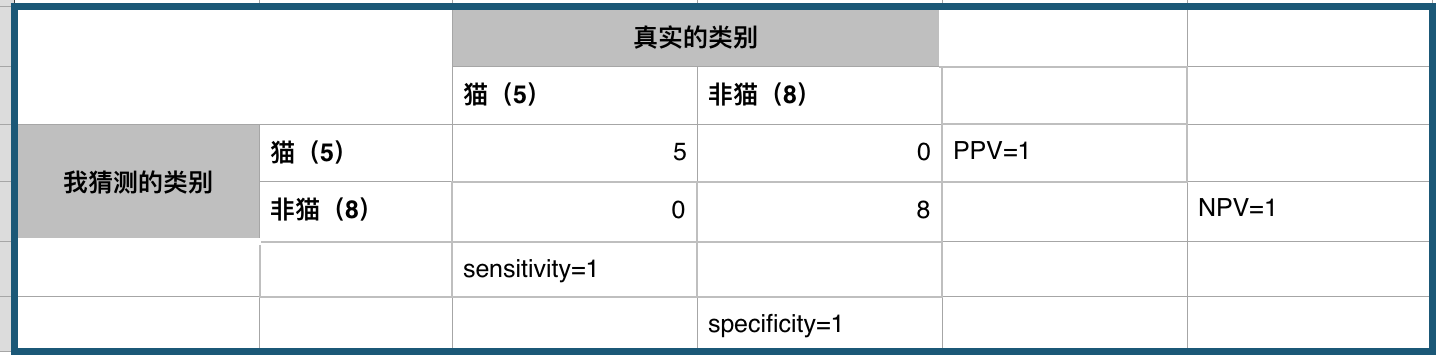
P = 5
N = 8
TP = 5
FP = 0
FN = 0
TN = 8
sensitivity = 5/5 = 1 # 正例找的夠全或者說我不會看漏正例
specificity = 8/8 = 1 # 反例找的也夠全或者說我不會看漏反例
PPV = 5/5 = 1 # 猜正例的時候一猜一個準或者說我猜它正例，它就不會是反例
NPV = 8/8 = 1 # 猜反例的時候一猜一個準或者說我猜它反例，他就不會是正例
acc = 13/13 = 1 # 全部猜對

激進的分類器

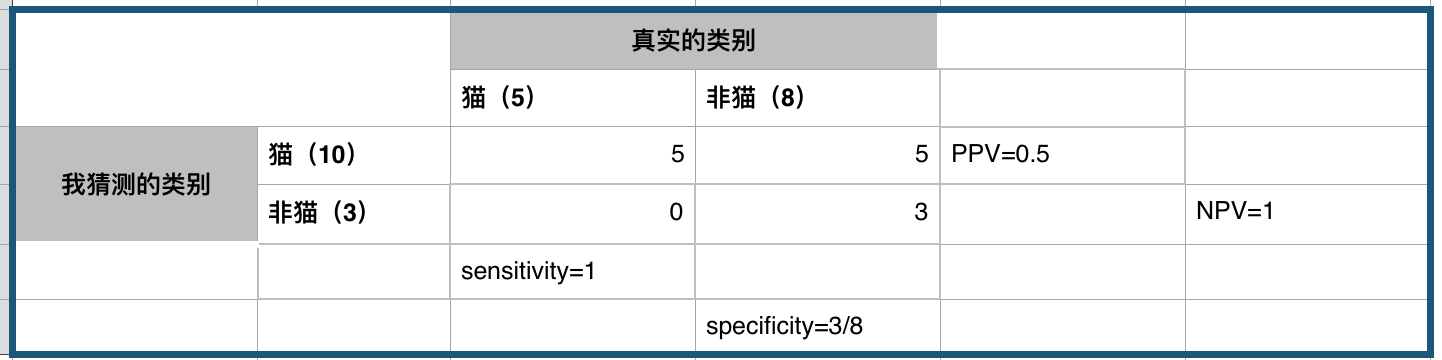
P = 5
N = 8
TP = 5
FP = 5
FN = 0
TN = 3
sensitivity = 5/5 = 1 # 正例找的夠全或者說我不會看漏正例
specificity = 3/8 # 反例找的不夠全
PPV = 5/10 = 0.5 # 猜正例的時候有一半機率猜對
NPV = 3/3 = 1 # 猜反例的時候一猜一個準或者說我猜它反例，他就不會是正例
acc = 8/13 # 總共猜對8例，猜錯5例，比隨機猜好一點點
轉載自：https://blog.csdn.net/leon_wzm/article/details/77524694