CPs中熱和電轉換原理

絕緣聚合物有共鍵價原子組成(類似於Si)， $sp^3$雜化的碳原子，共享電子被束縛在鍊形分子的低能量軌道上，導致導電率很低。但是在一些共軛聚合物(conjugated polymers), 比如聚乙炔(trans-polyacetylene), 碳原子 $s$

p 2 sp^2 雜化，在垂直於 $\sigma$鍵的方向形成 $\pi$

\pi 鍵。由於形成交疊區域，相鄰C原子的 $sp^2$雜化的 $p_{}$

z p_z 軌道，導致沿著聚合物主體方向，離域電子的移動， 在這種交替的 $\sigma$和 $\pi$分佈的C-atoms中，在激發光譜中，由於Peierls instability， $\pi-band$會被分成 $\pi-band(電子填充滿)和\pi^*band(無電子)$並有一個能量為 $E_g$的gap。與傳統的半導體相比，結合的軌道( $\pi$)對應於半導體中的價帶， 而未結合的軌道 ( $\pi^*$)對應於半導體中的導帶。相似的，在Highest Occupied Molecular Orbital (HOMO) 和 Lowest Unoccupied Molecular Orbital (LUMO)之間的能量 $E_g$，類似於半導體中的禁頻寬度 $E_g$。因此，共軛聚合物的導電率仍然很低，所以說 ，僅靠共軛聚合是不夠的，然而，導電率可以通過摻雜增強，但是由於CPs的structure-property relationships，摻雜有副作用。這將在section 4中導論。

1 Electrical conductivity 導電率

一般來說，可以使用電化學或化學方法對聚合物進行摻雜。兩種方法處理流程：

• (i) 一個單元結構(monomer)氧化的開始是從 $\pi-system$中除去電子，產生一個自由基(free radical)和無自旋的正電荷(spinless positive charge),減少的摻雜劑轉化為平衡離子，中和引入到 $\pi-electron$系統的正電荷。
• (ii) 電荷與自由基的區域性振動引起電荷和自由基的耦合，而這種耦合稱為極化(polaron)
• (iii)極化形式可以為自由基陽離子或自由基陰離子(radical cation or radical anion)，在帶隙內形成新的區域性電子態，低能態被單電子佔據，
• (iv)從極化子從除去或新增新的電子會進一步引起新的無旋缺陷，稱為雙極化，是一個與極化畸變(polaronic distortion)有關的自由基離子對,根據不同的聚合物的化學結構，可以受到其他3到4個單元結構(monomer)的影響。

[22]雙極化子的產生在熱力學上要比兩個極化子的產生更有用，因此，在高的摻雜水平下，兩個極化子變為一個雙極化子的可能性越大。

其實會聯絡到半導體中重摻雜下的能級交疊
但是如果摻雜濃度過高，雙極化能級會交疊，最終形成連續的帶。如下圖，並且雙極化之間的間隙也會增加因為新形成的雙極化子是以犧牲帶邊為代價而形成的，差雜濃度進一步增加，會導致雙極化帶的上邊界和下邊界分別和導帶和價帶結合，形成類似金屬的帶[7, 22]

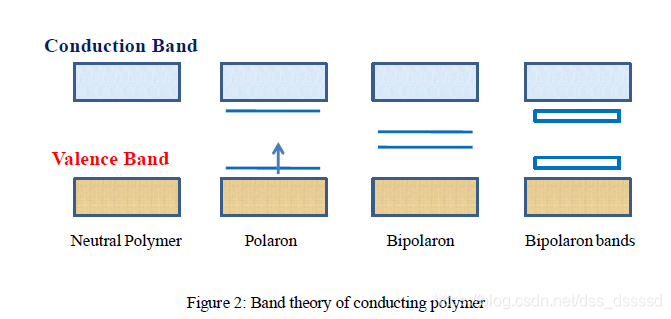
基態退化的共軛聚合物， 比如聚乙炔(polyacetylene)的導電機理可以使用稍微不同的機理解釋，由於氧化差雜導致極化子/雙極化子的產生 [20-21]。由於基態的退化，帶電的陽離子受束縛較弱，可以沿著鏈自由移動，這種電荷位置相互獨立，並隔離基態的兩相(自旋相反但能量相同)，稱為孤子(soliton)，有時是中性的。例如，
假設聚乙炔產生的孤子可以離域化的距離為12個C-H單元，並且最大的電荷密度與摻雜離子濃度相同。孤子的形成會在帶隙之間形成新的區域性態，隨著摻雜濃度的增加，就像雙極化子一樣，帶電的孤子可會與其他的孤子交疊形成孤子帶，最終會與導帶/價帶接觸，導致類似金屬的導電性。

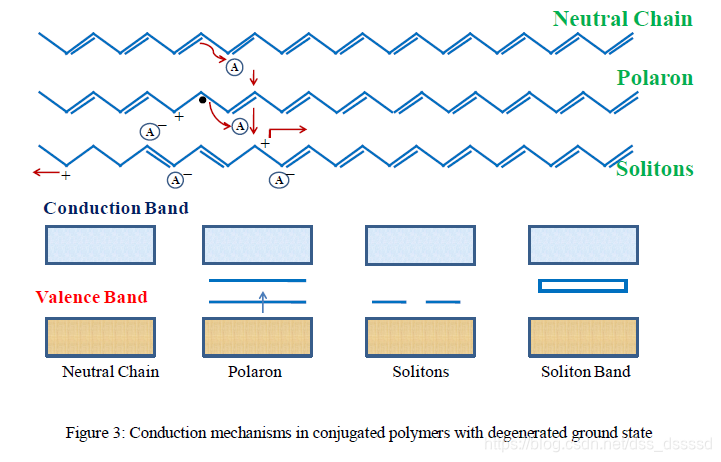
這種導電機理會受到CPs中的能量障礙和空間障礙影響。通過摻雜引入的額外載流子由於與反離子(摻雜劑)的靜電吸引而滯留在鏈中。[27, 86]在低介電常數(~3)中 ，低摻雜會產生大尺寸的陷阱，而這些陷阱會阻礙載流子的移動， 隨著摻雜濃度的增加，陷阱會交疊，他們之間的能量勢壘會降低。這種在 $\pi-軌道$上能量勢壘的降低會增強電子移動[11].通過增加差雜濃度實現，然而，空間障礙也會在原子核微觀尺度上影響你電荷傳輸，比如counter ions position,interchain distance, configuration of chains, size of crystalline and amorphous domains, orientation of crystallite。

在CPs中，電子傳輸是通過跳動過程(hopping process[2, 11-12])實現的,在非摻雜或低摻雜聚合物中， 在外電場作用下，極化子會跳躍到臨近的聚合物鏈的中性區域，
另一方面，在摻雜聚合物中，載流子(一對極化子和反離子)從一個極化子位點跳到另一個極化子位點，而構成跳躍位點的聚合物鏈不發生任何畸變。在無序或非晶的CPs中，溫度與導電率的關係使用VRH模型描述(variable range hopping),假設 constant density of states（定態密度）。
根據VRH模型， 溫度與導電率的關係如下:
$\sigma(T) = \sigma(0)exp(\lfloor -(T_0 / T)^{\lambda}\rfloor)$

$T_0$為莫特溫度值，
$T_0 = \frac{18}{L{_c^3N(E_F)K_B}}$
$L_c$為定域長度， $N(E_F)$為費米能級的態密度， $K_B$為玻爾茲曼常數。

適度摻雜和結構有序的CPs， 隨著鏈之間定域長度的增加，鏈之間的連線性更好，會導致很好的電轉移特性，
例如，高摻雜和高有序的CPs，比如樟腦磺酸摻雜的PANI(聚苯胺),在低溫下表現很好的金屬溫度依賴性。

2 seebeck cofficient 塞貝克係數

塞貝克係數是開環電壓(溫度熱端和冷端兩端之間的電壓 )和溫差之比，塞貝克係數有三種不同的貢獻因子：電子(electronic) 聲子(phonon)和電-聲子(electron-phonon),在金屬系統中存在大量的自由電子，電子主要貢獻塞貝克係數。電子從熱端移動到 冷端形成電勢，產生電子貢獻。在這種情況下，塞貝克係數與溫差成線性關係[14]
聲子貢獻主要認為聲子曳引效應(Phonon drag), 一般在低溫(<200k)比較明顯，在低溫時聲子平均自由程(phonon mean free path)比較大[7]。當聲子和電子的平均自由程可比擬時，電子-聲子散射變得重要[7, 11].好的晶體結構的高導電聚合物在低溫時有較好的電子-聲子散射[11, 12]。重摻雜的聚合物，比如polyacetylene(聚乙炔),polyaniline(聚苯胺),polypyrrole (聚吡咯)存在很小的正塞貝克係數( $&lt;14uV/K$在接近室溫時)，並且隨溫度有線性下降[7]。然而，由於電子-聲子作用可能會導致線性偏差。在輕摻雜的情況下，塞貝克係數要大於重摻雜[7, 12]，對於這種CPs，塞貝克係數隨著溫度可能非線性增加或降低。有時， 塞貝克係數非線性隨著 $T^{1/2}$非線性下降，這可以用區域性狀態之間的莫特變化範圍跳變傳輸解釋。區域性狀態內最鄰近跳躍使得塞貝克係數與溫度有 $1/T$的依賴關係，但是在重摻雜下，塞貝克係數隨著溫度線性增加[12, 24]

3 Thermal conductivity 熱導率

在無機材料中，熱導率中的電子部分與電導率耦合，而在有機材料中，由於更強的電荷-晶格耦合效應，這種協同效應無效（違反了Wiedemann-Franz law）。除此之外，由於與無機材料 相比，有機材料的電導率更低,因而電子對 $\kappa$的貢獻更低[16, 17]。在有機材料中，熱傳導主要依靠聲子(phonon)（比如，量子晶格振動）實現而不是電荷載流子(例如 $\kappa_l&gt;\kappa_e$)。對於CPs， $\kappa$不僅依賴於分子的重量和形狀，還依賴於鏈結構的不同。對於聚合物的主要鏈狀結構：

• Linear polymers
• Branch polymers
• Crosslinked polymers
• Network polymers
  如下圖(a)：
  

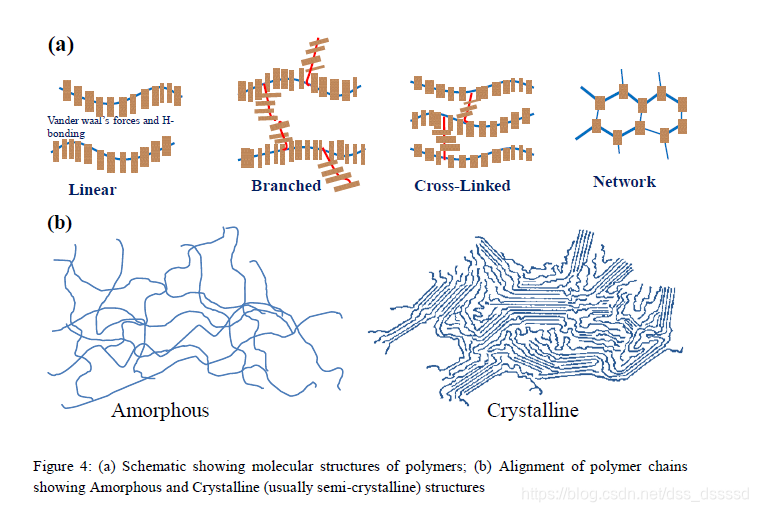
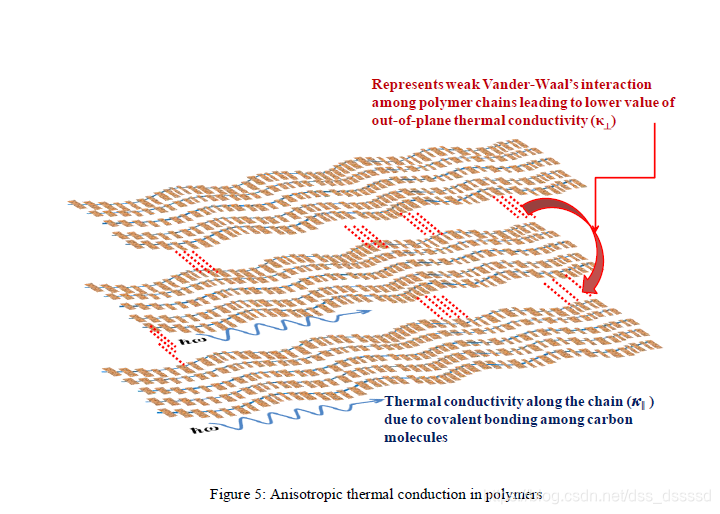
聚合物鏈有多種結構，結合會形成非晶(amorphous)或半晶結構(semi-crystalline), 如上圖(b)。不同的結構在熱導率和熱擴散上有各向異性[18-19]， 對於一個特定的CP，在更有序的鏈上，各向異性更明顯。

儘管這種各向異性(anisotropy)是排列整齊，有序的聚合物鏈的特點，但是在非晶結構上也存在。這可以解釋為熱傳輸機制在兩個方向上不同[18]。平面內導熱係數值高於橫向導熱係數，這是由於在聚合物鏈上的強C-C共價鍵作用，而不是通過垂直方向上的弱範德華分子相互作用傳遞熱能。如下圖：

機械形變(在拉伸力作用下)和沉積到基板上的不同方式(spin coatinng, screen printing)也可以將熱傳輸的各向異性引入到聚合物材料中.旋塗過程中的離心力導致平面內和平面間導熱性的不同[18]。值得注意的是，對於大多數CPs，即使 $\sigma$可以有三個數量級的增加， $\kappa$的變化也很小(比如， 從0.1W/mK到1.0W/mK)。由於CPs的 $\kappa$很小，所以測量過程更復雜。同時，導熱率的各向異性需要考慮在內[18, 19]。當 $\sigma$增加（>=100S/cm）時，也會導致 $\kappa_e$的增加，當 $\kappa_e$可以與 $\kappa_l$相比擬甚至超出時，在估計熱導率的時候也要考慮 $\kappa_e$了[11]。 $\kappa$與CPs的結晶程度也有關係， 比如在低結晶的CPs中，熱導率單調增加；而對於高結晶CPs，熱導率很高，隨著溫度升高（up to 100k）先增加後減小。低溫時熱導率的偶然上升可以解釋為聲子-聲子散射的抑制導致了聲子平均自由增加[11]。