基於Attention的機器翻譯模型,論文筆記
論文題目:Neural Machine Translation by Jointly Learning to Align and Translate
論文地址:http://pdfs.semanticscholar.org/071b/16f25117fb6133480c6259227d54fc2a5ea0.pdf
摘要
神經機器翻譯(Neural machine translation,NMT)是最近提出的機器翻譯方法。與傳統的統計機器翻譯不同,NMT的目標是建立一個單一的神經網路,可以共同調整以最大化翻譯效能。最近提出的用於神經機器翻譯的模型經常屬於編碼器 - 解碼器這種結構,他們將源句子編碼成固定長度的向量,解碼器從該向量生成翻譯。在本文中,我們推測使用固定長度向量是提高這種基本編碼器 - 解碼器架構效能的瓶頸,提出讓模型從源語句中自動尋找和目標單詞相關的部分,而不是人為的將源語句顯示分割進行關係對應。採用這種新方法,我們實現了與現有最先進的基於短語的系統相媲美的英文到法文翻譯的翻譯效能。此外,定性分析顯示模型發現的(軟)對齊與我們的直覺非常吻合。
簡介
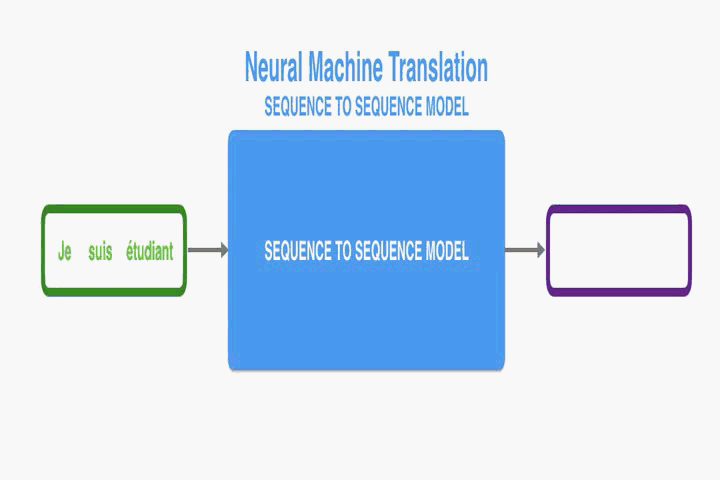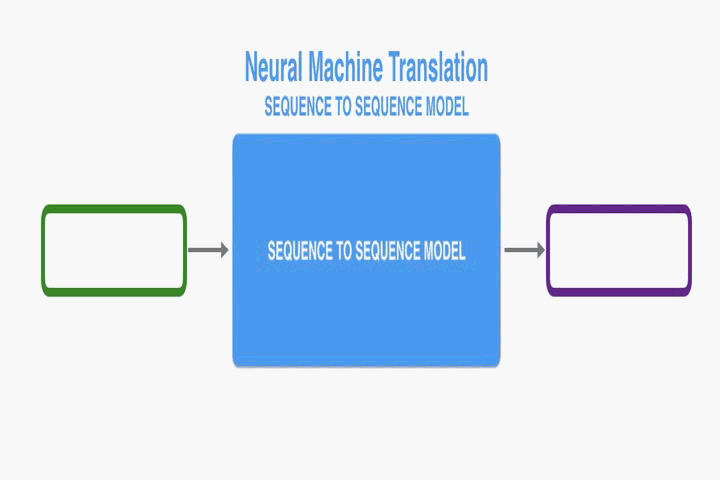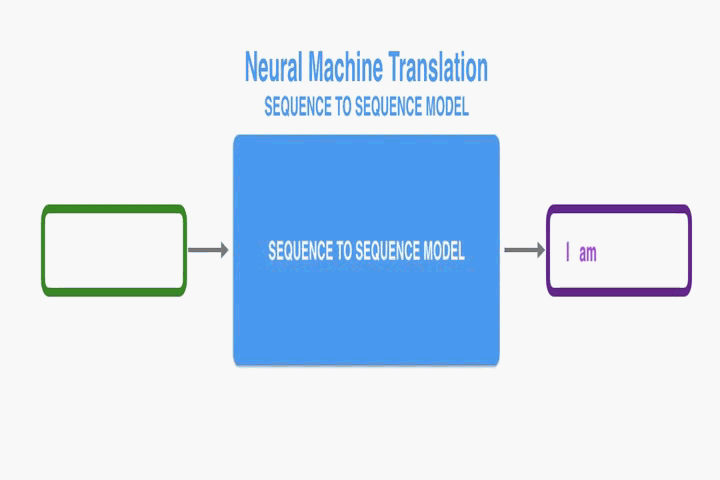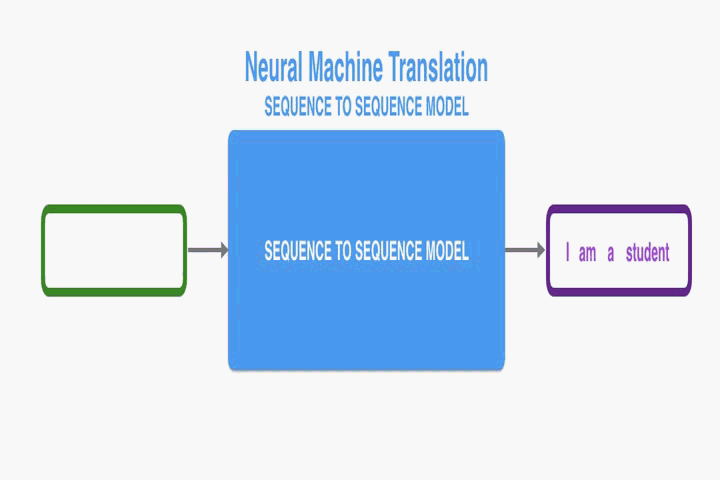
之前的NMT在處理長句子的時候會有些困難,尤其是比訓練資料集更長的文字。隨著資料句子長度增加,基本的編碼解碼器表現會急劇下降。因此,該論文提出將編碼解碼模型拓展,使其能夠連帶地學習去對齊和翻譯。每翻譯一個單詞,它就在源語句中查詢資訊最相關的位置集合。這個模型基於與這些源位置相關聯的上下文向量和所有之前形成的目標單詞預測目標單詞。
最大的區別在於它不是嘗試去把一整個輸入句子編碼為一個單一的固定長度的向量。而是把輸入的句子編碼為向量的序列,解碼翻譯的時候選擇這些向量的一個子集。這也就解放了NMT,不需要再把源語句所有的資訊,不管有多長,壓縮成一個固定長度的向量。這個模型對長句子表現要更好。不過任何長度上它的優勢都很明顯。在英法翻譯的任務中,這個方法可以媲美基於短語的系統。而且分析顯示這個模型在源語句和對應的目標語句之間的對齊效果更好。
背景:神經機器翻譯
從概率的角度上來說,機器翻譯的任務等同於找到一個目標序列,使得在給定源語句
的情況下生成
的概率最大。即:
,在NMT任務中,我們使用平行的訓練語料庫(即:x,y為相同內容的2種語言)來擬合引數化的模型,讓模型學習到能最大化目標語句的條件概率分佈。NMT一旦學會了這種條件概率分佈,那麼給予一個源語句,它都能通過搜尋找出條件概率最大的句子作為相應的翻譯。
RNN Encoder–Decoder:
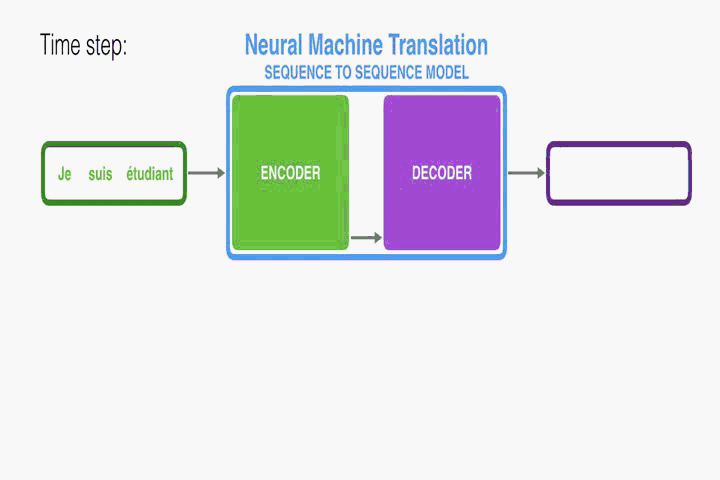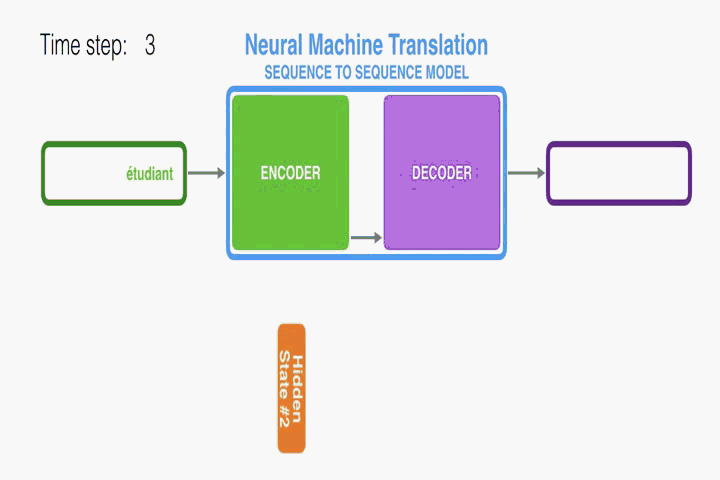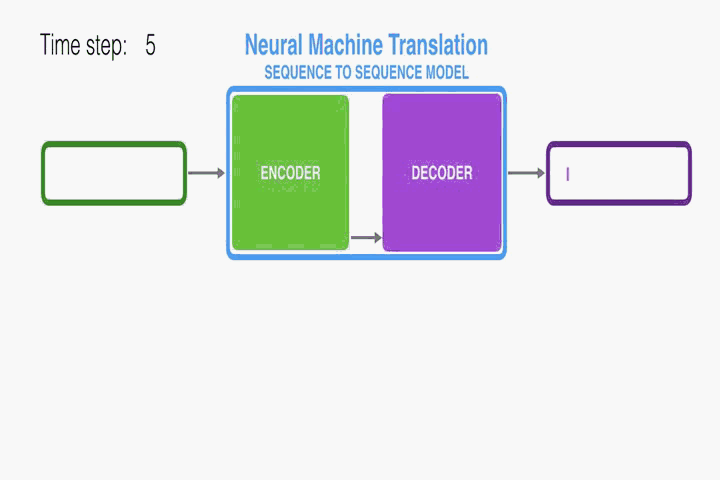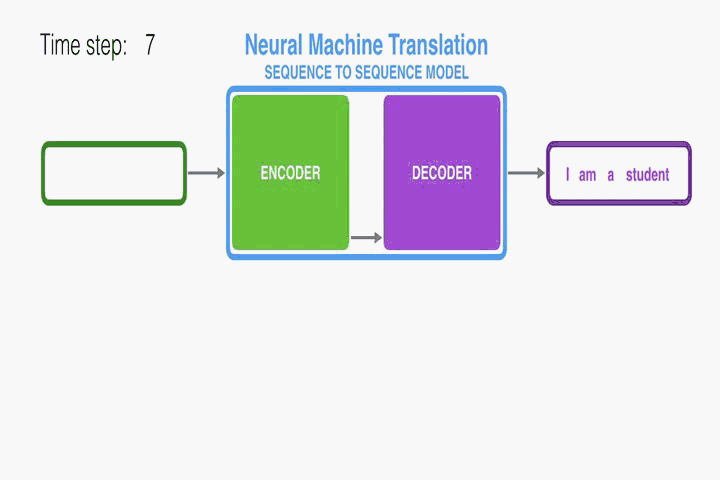
首先介紹一下本文使用的底層框架RNN Encoder–Decoder。本文是在此框架上進行修改從而提出的。Encoder讀取一個向量化的輸入序列
其中是時間
時刻下的hidden state,
是由hidden state組成的序列生成的向量。
和
是2個非線性的函式。例如:你可以使用LSTM作為函式
來得到hidden state,同時你可以使用
來作為
的函式。
Decoder一般情況下是通過訓練給定上下文向量和所有之前已經預測過的單詞
來預測下一個單詞
,換句話說,Decoder通過將聯合概率分解成有序條件來定義翻譯為序列
的概率:
(1)
其中,通過RNN,每個條件概率被建模為:
其中是一個非線性的(可能是多層的)函式,它的輸出指的是輸出結果為
的概率。
是RNN的hidden state。
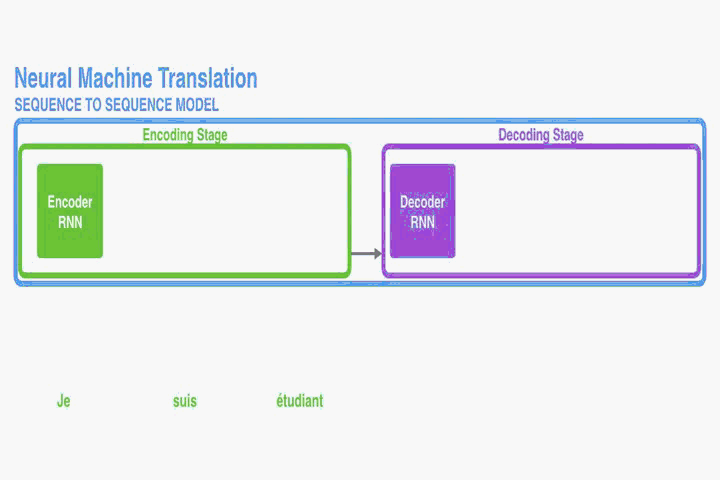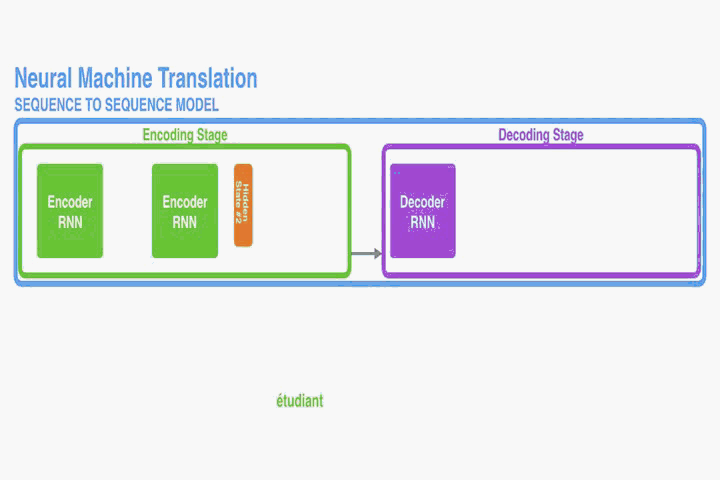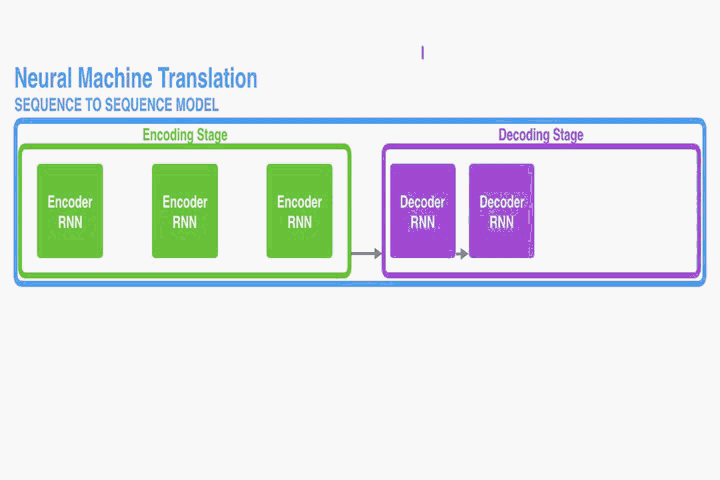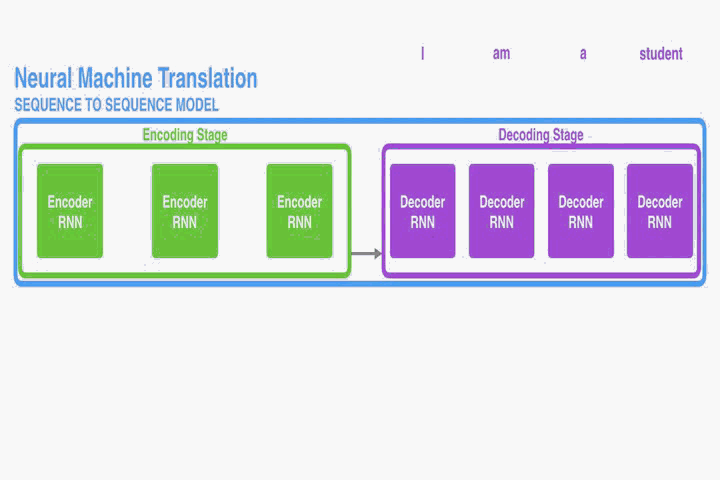
對齊翻譯結構
這部分提出一個NMT的新結構。這個新結構包括一個雙向RNN作為Encoder,一個模擬翻譯過程中通過源語句進行搜尋的Decoder。
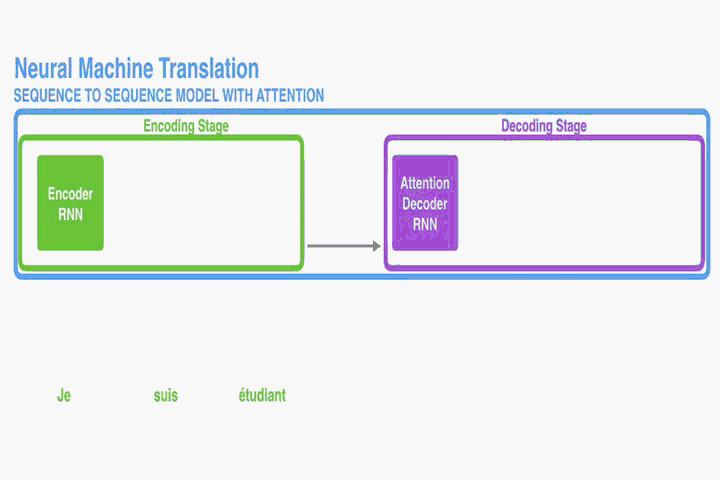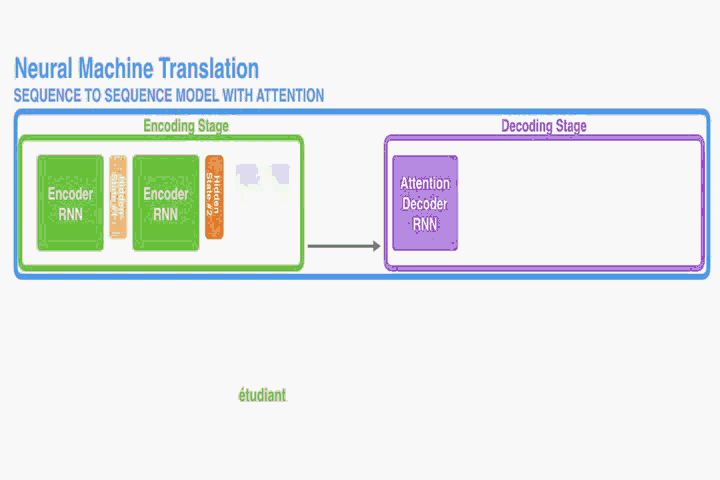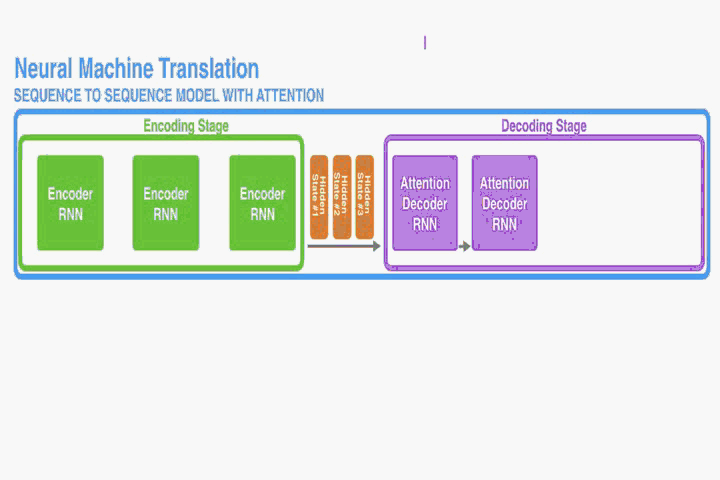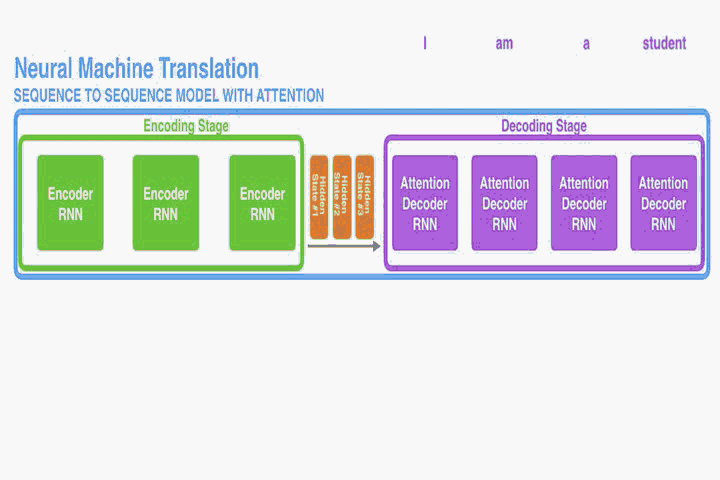
Decoder:
在這個新的結構中,我們對公式(1)中的條件概率分佈做了新的定義:
其中,是時間
時RNN的hidden state,由公式:
需要注意的是,與現有的Encoder–Decoder模式不同(如上節),這裡概率是針對每個目標字的不同的上下文向量
。上下文向量
取決於Encoder將輸入句子對映到的annotations(即序列
)。在annotations中,每個
包含了整個輸入序列的資訊,但重點關注(Attention)輸入序列中第
個單詞周圍的部分。下一節會介紹annotations的計算方法。這一節我們先預設我們已知annotations。

觀察上圖,上下文向量實則是對annotations序列
的逐個加權求和:
每個的權值
的計算:
其中
是一個對齊模型,它可以評估值位置
周圍的輸入和位置
的輸出匹配程度。對匹配程度的打分依賴於RNN hidden state(
)和輸入序列的第
個的值
。

我們將對齊函式引數化為一個前饋神經網路,讓它和本文中的其它模組聯合訓練。需要注意的是,不同於傳統的機器翻譯,這裡的對齊值不再被視為潛在的變數。與之相反,對齊模型定向地計算一個柔和的對齊,這就允許代價函式的梯度反向傳播。這個梯度就可以隨著整個翻譯模型一起訓練這個對齊模型。
我們可以將所有對annotations加權求和的方式看做是在計算數學期望,並且期望值是可能在對齊值之上的。設為目標單詞
與源詞
對齊的概率,(通俗說就是
的翻譯結果為
的概率),然後,第
個上下文向量
是所有具有概率的
的數學期望。
概率(或者說
)反映了在決定下一個狀態
和生成
的時候,考慮到之前的hidden state (
)的 annotation
的重要性。直觀地說,這實現了Decoder中的Attention機制。 Decoder決定了源語句的哪些部分需要注意。 通過讓Decoder具有注意力機制,我們可以免除Encoder將源句子中的所有資訊編碼成固定長度向量的負擔。 有了這個方法,資訊就可以在annotations序列中傳播,也可以被Decoder選擇性地恢復。
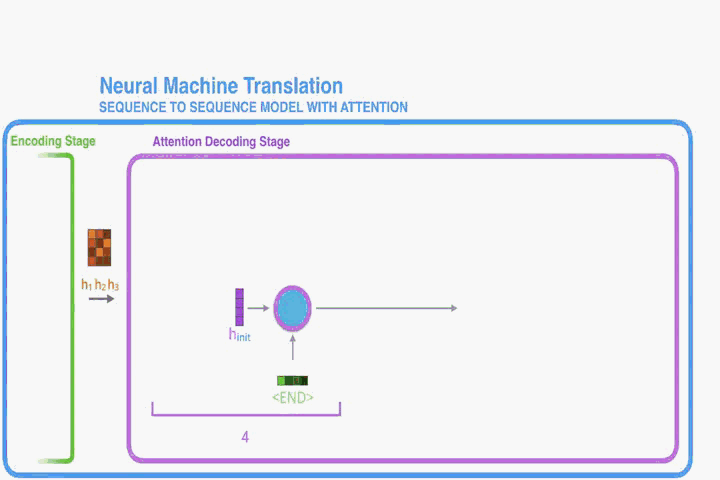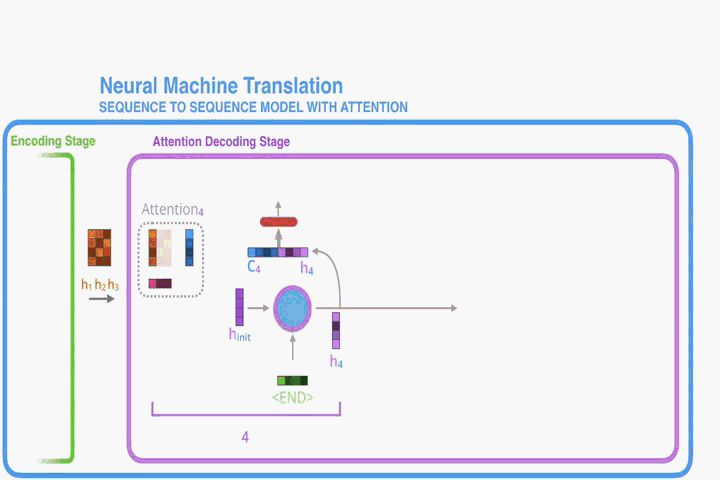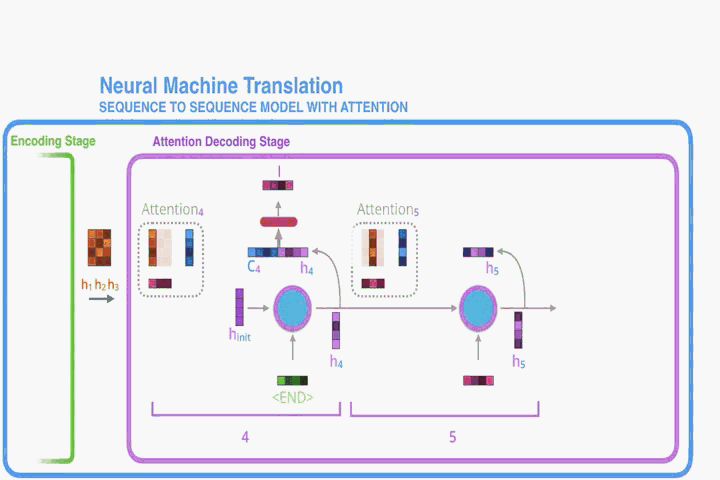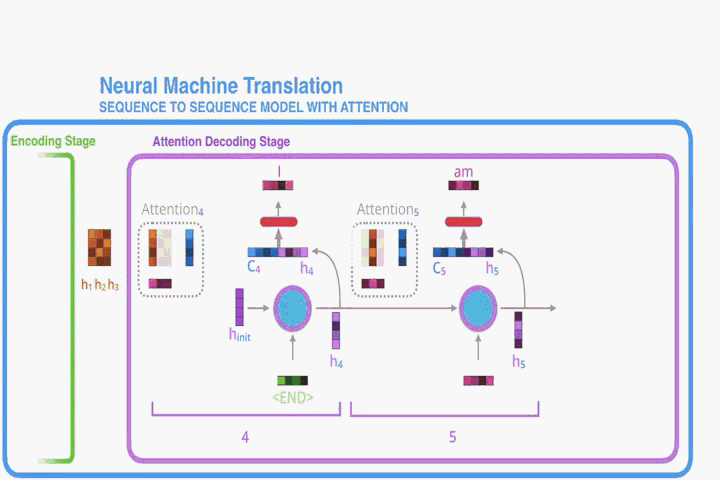
Encoder: Bidirectional RNN for Annotating Sequences
一般的RNN模型,是按順序由開始位置到結束位置
讀取的。然而在本文提出的結構中我們希望每個單詞的annotations不僅能總結前面的單詞,而且能總結後面緊跟著的單詞。因此,在此處我們將使用雙向RNN(Bi-RNN)。
如圖一,Bi-RNN包含了前向hidden states和反向hidden states,其讀取序列的方式是正好相反的,舉個例子對於一句話“我愛祖國”,前向做的讀入順序為(我,愛,祖,國)和反向讀入順序為(國,祖,愛,我)。
我們通過連線前向隱藏狀態和後向隱藏狀態來獲得每個單詞的annotations,可以表示為:
![]() ,通過這個方式,annotations
,通過這個方式,annotations 將集中在
的周圍單詞上。Decoder和對齊模組稍後會使用該序列來計算上下文向量
。
結構介紹:
RNN
當前狀態:
更新狀態:
更新門:
重置門:
對齊模型
