基於自動分段最小二乘法對股票的多項式曲線擬合

摘 要 針對傳統的分段最小二乘法確定分段步長時經驗成分較多的不足，提出一種通過比較擬合優度，自動確定相對最優的步長。通過實際資料的驗證，驗證了此方法的擬合效果。

關鍵詞  分段擬合  多項式曲線  最小二乘法

引言

    在對股票趨勢的預測中，常常需要從一組帶噪聲的股票歷史資料（x_i,y_i）;i=1,2,…,n中找出自變數x和因變數y之間隱含的函式關係，其中利用最小二乘法對股票歷史資料進行多項式曲線擬合是一種比較簡單的資料擬合方法。當資料點較多時，多項式的階數太低，擬合效果不太理想。而要提高擬合效果就需要提高曲線階數，但多項式階度太高又會帶來計算上的複雜以及其他方面的不利^[1]

為解決上述問題，可採用分段曲線擬合，在每段區間上進行區域性最小二乘擬合。而分段點的選擇對擬合效果至關重要，文獻[2]提出五個資料點擬合一條三次曲線（曲線邊界點取一個數據點），但這種發放分段區間太密，過於依賴主觀經驗。文獻[3]中提出求得起點和終點的座標以及下一點和起點之間的連線與所擬合出的直線的夾角ε，根據ε是否大於設定的閾值來決定是否設該點為分段點。但這種方法只適合資料變化比較慢的情況。本文針對股票資料量大、變化快的特點，提出了根據擬合優度來自動識別分段點的方法。下面根據如表1中的資料，對該方法進行說明。

表1 中國平安三月份漲跌幅度

1 一般的最小二乘法

    一般最小二乘法對多項式曲線進行擬合時，通過求得所有資料的最小殘差平方和來確定多項式的引數。

    給定函式y=f(x)在點x₁…x_n的函式值y₁…y_n，求多項式。使得 

則 

將方程整理，得到

求解方程得到a₀ ，a₁，…，a_m，從而得到最小二乘擬合多項式y(x)=a₀+a₁x+…+a_mx^m

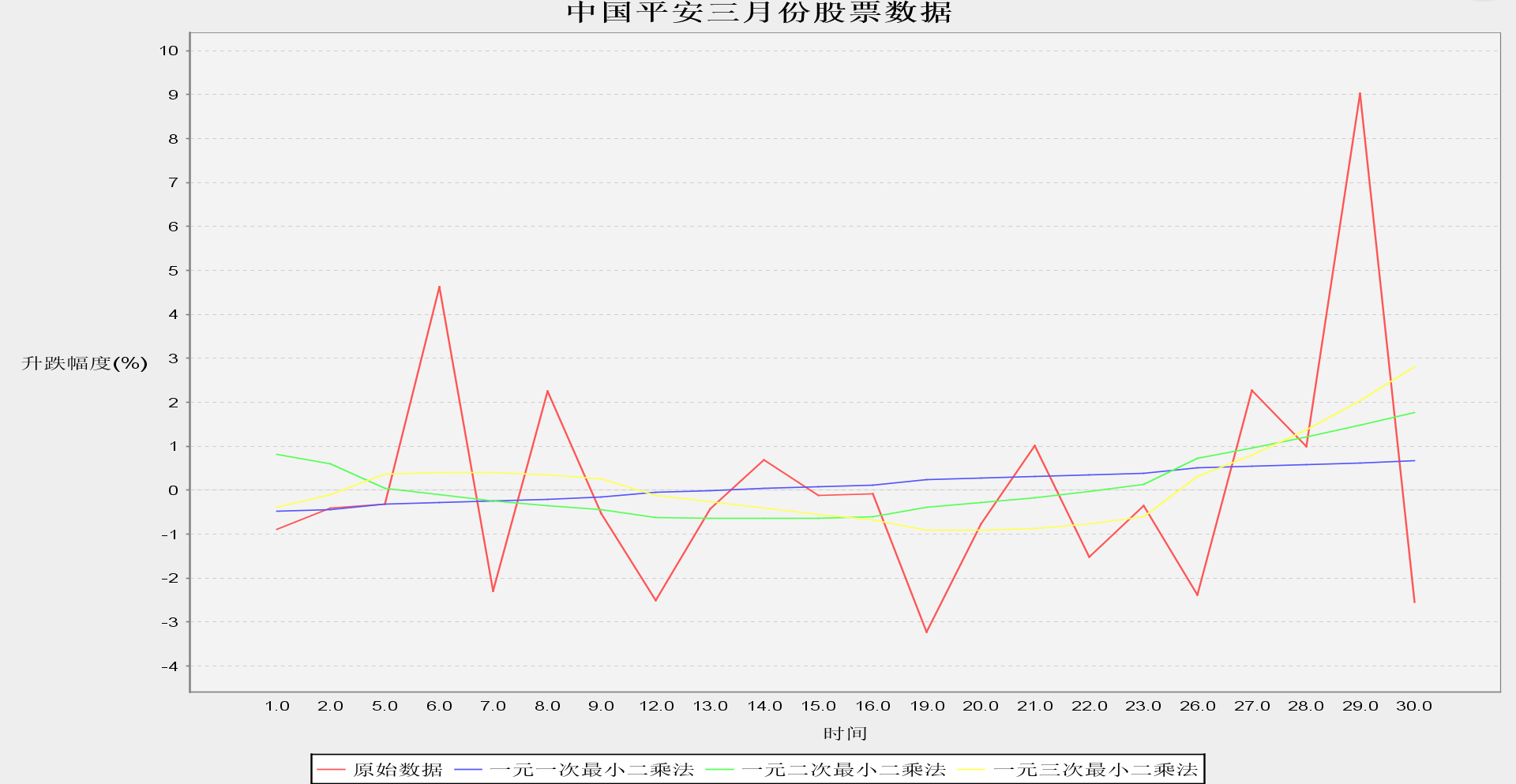
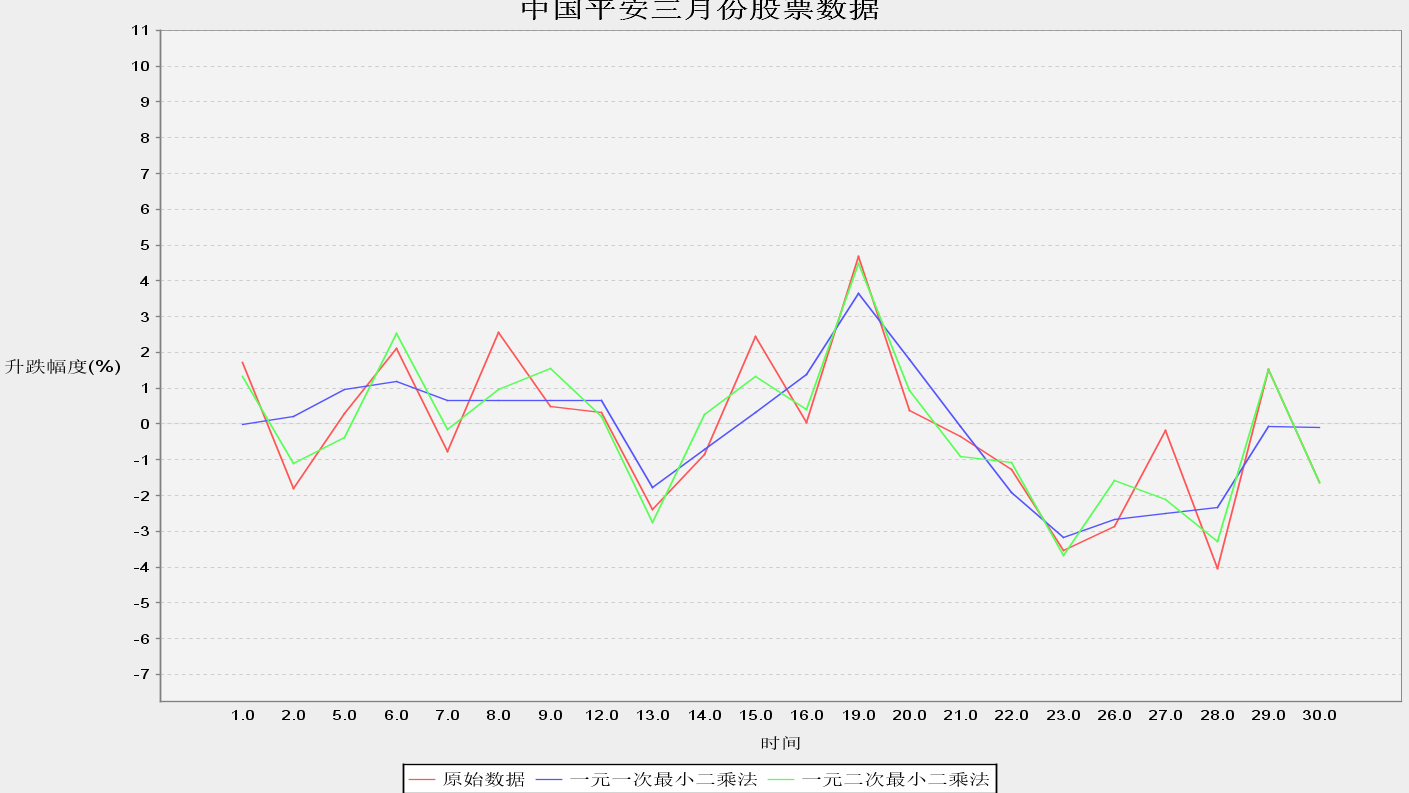
本文通過以中國平安三月份股票資料為例，利用一般的最小二乘法對股票資料進行曲線擬合（如圖1）。發現雖然只能大致擬合出曲線的趨勢，對股票資料的變化拐點無法進行預測。

圖1 普通最小二乘法曲線擬合

2 固定步長的分段最小二乘法

針對普通最小二乘法只能擬合股票資料的趨勢，對股票拐點不敏感的問題，選用了分段最小二乘法，分段最小二乘法能通過減少資料集，簡化了數學模型，減低了多項式項數，從而減少了運算量^[4]。具體方法是：

1）  假定有n條股票資料，步長為i，將股票資料按確定的步長i分為e=n/i+1組。

2）按一般最小二乘法的方法求得每組多項式曲線的係數，最終得到最後的擬合曲線。

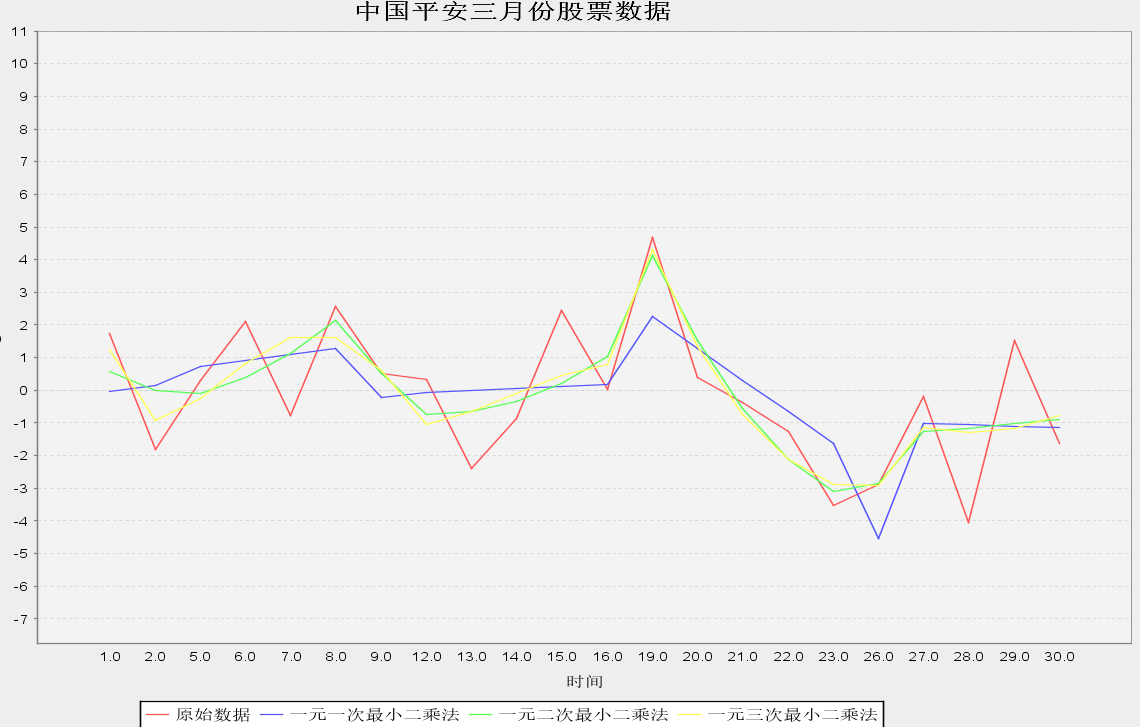
本文中分別選定了步長為6和步長為8（如圖2、3），可以看出，步長越小，與歷史資料曲線逼近度越高，當然這也存在一些問題，當步長選擇過小時，雖然擬合曲線與歷史資料曲線很相似，但是卻失去了預測股票的初心。而步長選擇過大時對曲線的擬合效果就比較差，所以當選用固定步長的分段最小二乘法時，非常依靠選定步長人的經驗，在對非常多的股票進行曲線進行擬合時效率將會特別低。

圖2步長為6的最小二乘法曲線擬合

圖3 步長為8的最小二乘法曲線擬合

3 自動分段最小二乘法

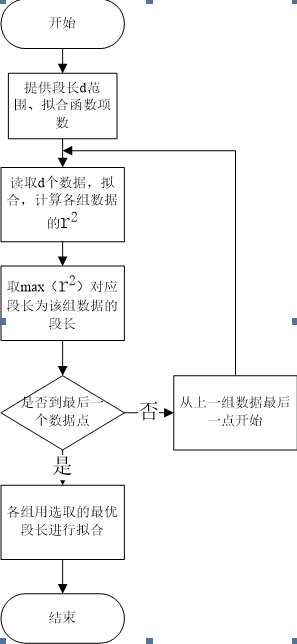
先給定一個段長的範圍（本實驗中段長d為4-8），評價擬合效果的擬合優度^[5]為r²，然後將所提供的股票資料依次取段長d個數據，對著幾組資料通過一般最小二乘法進行多項式曲線擬合，計算擬合優度 （y為真實值，y_c為估計值，為平均值），取max（r²）對應的一組資料為此次擬合的樣本值，這次得到的模型就是第一段曲線的模型。將從這段曲線的最後一點開始重複進行前面所需的擬合和判斷，直到所有點擬合完畢，得到所有分段曲線的模型。以上步驟總結出演算法流程如圖4所示。

圖4 分段擬合流程圖

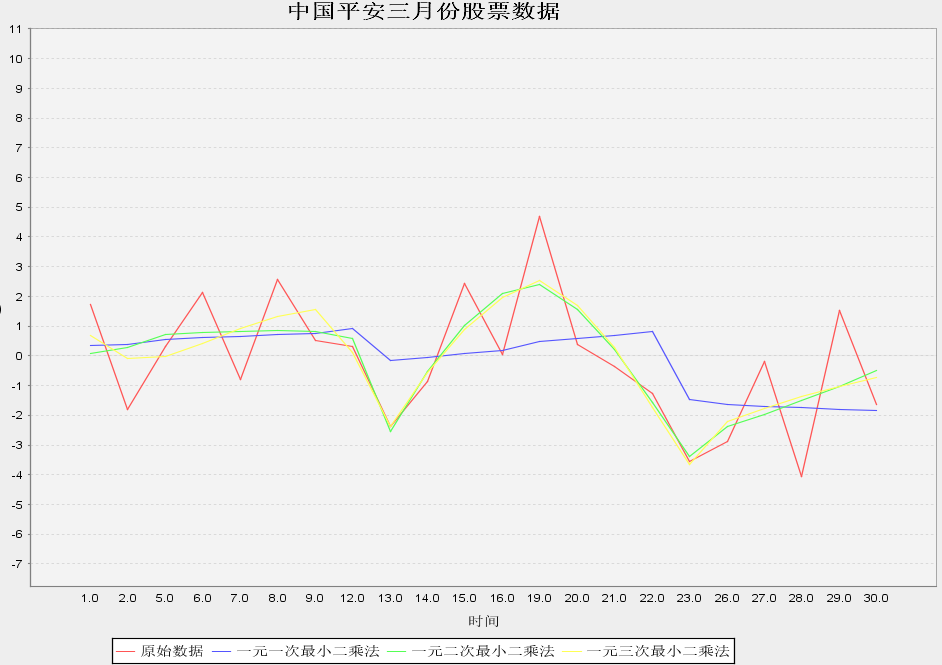
根據自動分段最小二乘法對股票資料擬合曲線如圖5所示，可以看出相比一般的最小二乘法和固定段長的最小二乘法擬合精度更高，能更好的擬合股票歷史資料。

圖5 自動分段曲線擬合

結語

       由上文實驗結果可知，自動分段最小二乘法相比一般最小二乘法和固定步長的最小二乘法相比，擬合效果更好，對批量資料擬合時效率更高。但是也存在很多缺點，考慮對股票的影響因素少，更多的是擬合曲線，對股票未來走勢預測的功能不好。

參考文獻

[1] 劉霞,王運鋒.基於最小二乘法的自動分段多項式曲線擬合方法研究[J].科學技術與工程,2014,14(03):55-58.
[2] 蔡山,張浩,陳洪輝,沙基昌.基於最小二乘法的分段三次曲線擬合方法研究[J].科學技術與工程,2007(03):352-355.
[3] 田壠,劉宗田.最小二乘法分段直線擬合[J].電腦科學,2012,39(S1):482-484.
[4] 劉曉莉,陳春梅.基於最小二乘原理的分段曲線擬合法[J].伊犁教育學院學報,2004(03):132-134.
[5] 王重,劉黎明.擬合優度檢驗統計量的設定方法[J].統計與決策,2010(05):154-156.