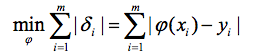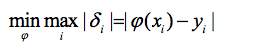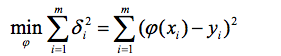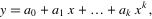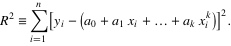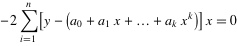基於迴歸曲線擬合模型的ALS(最小二乘法)推導過程以及Python實現
概念
最小二乘法(Alternative -Least-Squares)是一種迭代演算法。它通過最小化誤差的平方和尋找資料的最佳函式匹配。利用最小二乘法可以簡便地求得未知的資料,並使得這些求得的資料與實際資料之間誤差的平方和為最小。最小二乘法可用於曲線擬合。
二乘法曲線擬合:根據給定的n個點,並不要求這條曲線精確地經過這些點,而是曲線y=f(x)的近似曲線y= φ(x)。
原理
給定數n個數據點p(xi,yi),其中i=1,2,…,n。求近似曲線y= φ(x)。並且使得近似曲線與y=f(x)的偏差最小。近似曲線在點p處的偏差δi= φ(xi)-yi,i=1,2,…,n。
常見的擬合方法有:
- 使偏差絕對值之和最小
- 使偏差絕對值最大的最小
- 使偏差平方和最小
按偏差平方和最小的原則選取擬合曲線,並且採取二項式方程為擬合曲線的方法,稱為最小二乘法
推導過程
- 設擬合多項式為:
- 各點到這條曲線的距離之和,即偏差平方和如下:
為了求得符合條件的a值,對等式右邊求ai偏導數,因而我們得到了:
將等式左邊進行一下化簡,然後應該可以得到下面的等式:
-
- 把這些等式表示成矩陣的形式,就可以得到下面的矩陣:
- 將這個範德蒙得矩陣化簡後可得到:
- 也就是說X*A=Y,那麼A = (X’*X)-1*X’*Y,便得到了係數矩陣A,同時,我們也就得到了擬合曲線。
實現
相關推薦
基於迴歸曲線擬合模型的ALS(最小二乘法)推導過程以及Python實現
概念 最小二乘法(Alternative -Least-Squares)是一種迭代演算法。它通過最小化誤差的平方和尋找資料的最佳函式匹配。利用最小二乘法可以簡便地求得未知的資料,並使得這些求得的資料與實際資料之間誤差的平方和為最小。最小二乘法可用於曲線擬合。
ML基礎教程:泛化與過擬合、正規化最小二乘法
泛化與過擬合 olympval.m Load the Olympic data and extract the training and validation data load data/olympics x = male100(:,1); t
簡單線性迴歸-最小二乘法推導過程
最近學習線性迴歸,自己推導了一下最小二乘法。 其他參考文章: https://blog.csdn.net/chasdmeng/article/details/38869941?utm_source=blogxgwz0 https://blog.csdn.net/iter
一元線性迴歸模型與最小二乘法及其C++實現
監督學習中,如果預測的變數是離散的,我們稱其為分類(如決策樹,支援向量機等),如果預測的變數是連續的,我們稱其為迴歸。迴歸分析中,如果只包括一個自變數和一個因變數,且二者的關係可用一條直線近似表示,這種迴歸分析稱為一元線性迴歸分析。如果迴歸分
線性迴歸模型和最小二乘法
1. 線性迴歸基本概念 線性迴歸假設因變數與自變數之間存線上性關係,因變數可通過自變數線性疊加而得到,即因變數和自變數之間可用如下方式表示。 式中為自變數,為權重係數,為偏置。 線性迴歸就是要解決如何利用樣本求取擬合出上述表示式,獲得最佳直線的問題,最常用的就是最小二乘法。 最
有監督迴歸:約束條件下的最小二乘法
1.前言 前面介紹的最小二乘學習法,是眾多機器學習演算法中極為重要的一種基礎演算法。但是,單純的最小二乘法對於包含噪聲的學習過程經常有過擬合的弱點。如下圖所示: 這往往是由於學習模型對於訓練樣
基於自動分段最小二乘法對股票的多項式曲線擬合
基於自動分段最小二乘法對股票的多項式曲線擬合 摘 要 針對傳統的分段最小二乘法確定分段步長時經驗成分較多的不足,提出一種通過比較擬合優度,自動確定相對最優的步長。通過實際資料的驗證,驗證了此方法的擬合效果。 關鍵詞 分段擬合 多項式曲線 最小二乘法 引言
曲線擬合的最小二乘法(基於OpenCV實現)
在科學實驗資料處理中,往往要根據一組給定的實驗資料,求出自變數x與因變數y的函式關係,這是為待定引數,由於觀測資料總有誤差,且待定引數ai的數量比給定資料點的數量少(即n<m),因此它不同於插值問題.這類問題不要求通過點,而只要求在給定點上的誤差的平方和最小.當時,即
曲線擬合的最小二乘法(基於OpenCV實現)的,擬合影象中離散點的擬合直線
今天使用擬合的最小二乘法,求出了給定的一組座標系上的點對最接近的直線的。 其具體理論如下: 在科學實驗資料處理中,往往要根據一組給定的實驗資料,求出自變數x與因變數y的函式關係,這是為待定引數,由於觀測資料總有誤差,且待定引數ai的數量比給定資料點的數量少(
最小二乘法多項式曲線擬合原理與實現 zz
博客 del p s 並且 多項式 聯網 python mar 程序 概念 最小二乘法多項式曲線擬合,根據給定的m個點,並不要求這條曲線精確地經過這些點,而是曲線y=f(x)的近似曲線y= φ(x)。 原理 [原理部分由個人根據互聯網上的資料進行總結,希望對大
最小二乘法進行曲線擬合 Python
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
數字訊號處理:曲線擬合演算法-----最小二乘法
在迴歸分析中,一般任意的資料都可以用一條曲線來表示,這個曲線可以用某一個高次方的代數多項式 y= a + b*x + c*(x)2 + ...來描述,其中 a , b , ...是常數。但是這樣通過每個點的曲線是沒意義的,也不能表示y和x的真實的相關關係。趨勢
基於OpenCV資料結構最小二乘法擬合圓-程式碼部分
對於網上常用的擬合圓程式碼(經過修改, 因為除數可能為0) /* * 參考: http://blog.csdn.net/liyuanbhu/article/details/50889951 * 通過最小二乘法來擬合圓的資訊 * pts: 所有點座標 * center: 得到
移動最小二乘法(MLS)曲線曲面擬合C++程式碼實現
移動最小二乘法(MLS)曲線曲面擬合 曲線曲面擬合有很多種方法,Beizer,B樣條等,曲面擬合移動最小二乘法是一個很好的選擇,本文會詳細講解一下移動最小二乘法方法擬合曲面,並給出C++程式碼實現。 本文首先是最小二乘法的分析,然後是畫曲面曲線圖。 目錄
哈工大《機器學習》最小二乘法曲線擬合——實驗一
程式碼更多細節待更新。 目標: 掌握最小二乘法求解(無懲罰項的損失函式)、掌握加懲罰項(2範數)的損失函式優化、梯度下降法、共軛梯度法、理解過擬合、克服過擬合的方法(如加懲罰項、增加樣本) 已完成的要求: 生成資料,加入噪聲; 用高階多項式函式擬合曲線; 用解
最小二乘法多項式曲線擬合原理與實現(錯誤地方已經修改底層補充自己寫的java實現)
也可使用Apache開源庫commons math,提供的功能更強大, http://commons.apache.org/proper/commons-math/userguide/fitting.html package com.fjsh.algorithm.leastSquareMethod.d
(C#)曲線擬合的最小二乘法
using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace 數值分析實驗報告 { class Gauss曲線擬合的最小二乘法
最小二乘法曲線擬合原理與實現
最小二乘學習法是對模型的輸出和訓練集輸出的平方誤差為最小時的引數進行學習,式中之所以加上係數1/2,是為了約去對進行微分時得到的2。 “LS”是Least Squares的首字母。平方誤差是殘差的範數,因此最小二乘學習法有時也稱為損失最小化學習法。
如何使用線性代數實現最小二乘法擬合曲線
也許在我們讀高中的時候,就知道在數學的世界裡,有一種直線擬合的方式:最小二乘法。它是一種數學優化技術,原理是通過最小化誤差的平方和尋找資料的最佳函式匹配。 比如研究x和y之間的關係,假設我們擁有的資料是將這些資料描繪在x-y直角座標系中,發現這些點並沒有能夠連線成一條直線。
最小二乘法多項式曲線擬合原理與實現
程式碼: # coding=utf-8 ''' 作者:Jairus Chan 程式:多項式曲線擬合演算法 ''' import matplotlib.pyplot as plt import math import numpy import random fig = plt.figure() ax =