上一篇文章《從零開始一起學習SLAM | 為啥需要李群與李代數？》以小白和師兄的對話展開，受到了很多讀者的好評。本文繼續採用對話的方式來學習一下相機成像模型，這個是SLAM中極其重要的內容，必須得掌握哦~

小白：師兄，上次聽你講了李群李代數，有種“聽君一席話勝讀十年書”的趕腳~後來看書感覺容易理解多了呢！
師兄：是嗎？那太好啦，給你講的過程也加深了我的理解呢
小白：那師兄今天要不要繼續加深理解一下相機成像模型 的部分呢？
師兄：額。。好啊（感覺被套路了，不過想想上次小白師妹請客吃了燒烤呢）
小白：講完一起吃飯去~
師兄：好呀好呀！

小孔成像
師兄：相機成像模型我們主要介紹針孔相機。中學時我們都學過小孔成像，還記得吧。像下面這個圖，就是小孔成像示例。你看三維空間的蠟燭在帶有小孔的黑箱子裡成像一個倒立是像，這個是實像

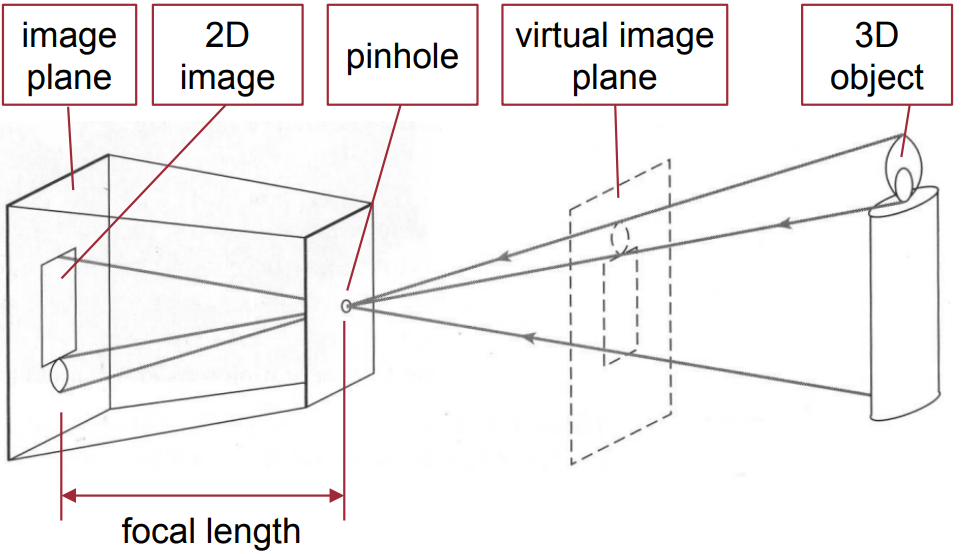
小白：嗯嗯，還有印象，那個正立的虛線畫的就是虛像吧
師兄：是的。話說幾千年前人們就發現了這個現象了~

小白：那師兄為啥要畫這個虛像呢？
師兄：因為這個虛像和實像是完全對稱的，數學上可以等價，後面我們推導公式的時候比較方便。
小白：這樣啊，還有個問題，為啥我看好多書上提到相機模型都是講的針孔相機？
師兄：因為自然界中這個成像過程最普遍，我們普通的相機，視場角不太大的話都符合針孔相機成像模型
小白：可是，普通相機好像沒有針孔那麼小。。。
師兄：哈哈，這個針孔是個類比，比如手機攝像頭鏡頭相對於被拍攝物體到手機的距離就非常小了，可以近似為一個針孔的
小白：糗大了。。。
師兄：沒事，不懂就問不能不懂裝懂嘛。我們繼續，前面針孔相機用數學表達就是下面這樣。我們把倒立的實像去掉，用正立的虛像代替就行啦。三維空間的點大P在成像平面上成的像就是小p了。大P，小p還有相機中心C在同一條直線上。

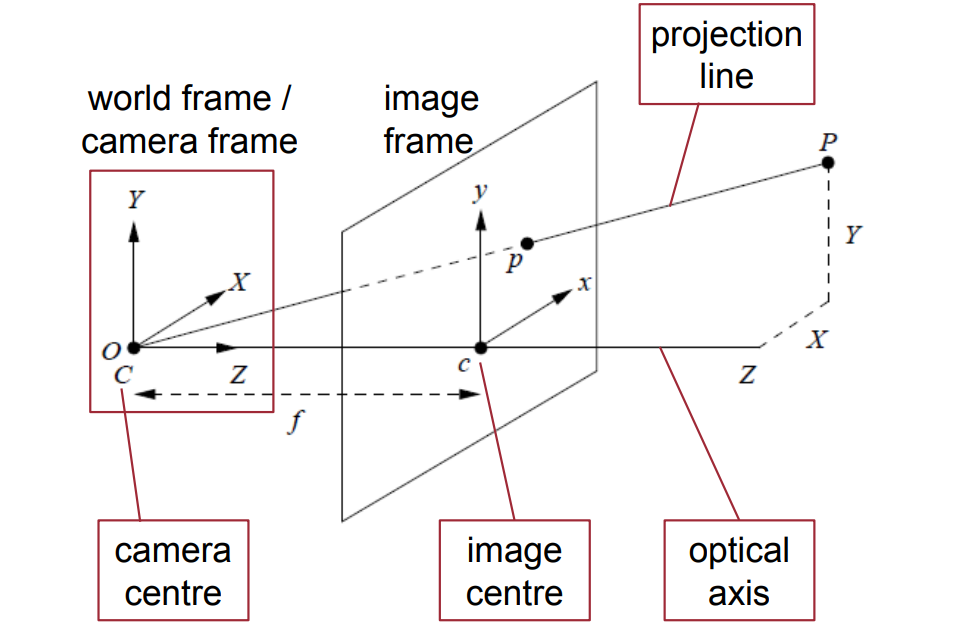
小白：嗯，這個圖還挺直觀的

紛繁複雜的座標系
師兄：下面我們即將進入公式的世界，yeah~
小白：師兄，我數學是語文老師教的。。。儘量通俗易懂的講哈
師兄：嗯，第一步，我們先要明白，這個三維空間有好多座標系，一個，兩個。。大概有三四個吧。
小白：（捂臉）
師兄：首先說兩個，世界座標系和相機座標系。顧名思義：

世界座標系(world coordinate system)：就是使用者定義的三維世界的座標系，以某個點為原點，為了描述目標物在真實世界裡的位置而被引入。單位為m。
相機座標系(camera coordinate system)：就是以相機為原點建立的座標系，為了從相機的角度描述物體位置而定義，作為溝通世界座標系和影象/畫素座標系的中間一環。單位為m。

小白：師兄，你說的好學術啊，這倆有啥不一樣？
師兄：舉個栗子吧。比如姚明要開始100米跨欄了，我們可以定義那個起點就是世界座標系原點。。
小白：打住。。。姚明好像是打籃球的吧？
師兄：哦哦，對，說錯了，是劉翔在世界座標原點（在師妹面前糗大了）。那麼，那麼那個拍照的攝影師，對，那個攝影師假如是姚明，那麼姚明所在的位置就是相機座標系的原點，這時候劉翔在相機座標系中就不是原點了。
小白：理解~
師兄：我們舉個普通的例子，比如下面這個圖，最右上方的那個點在三維空間中，如果以世界座標系為原點，它的座標就是Xw，如果以相機座標系為原點，它的座標就是Xc，我們可以通過旋轉R和平移t來把世界座標系轉換到和相機座標系重合

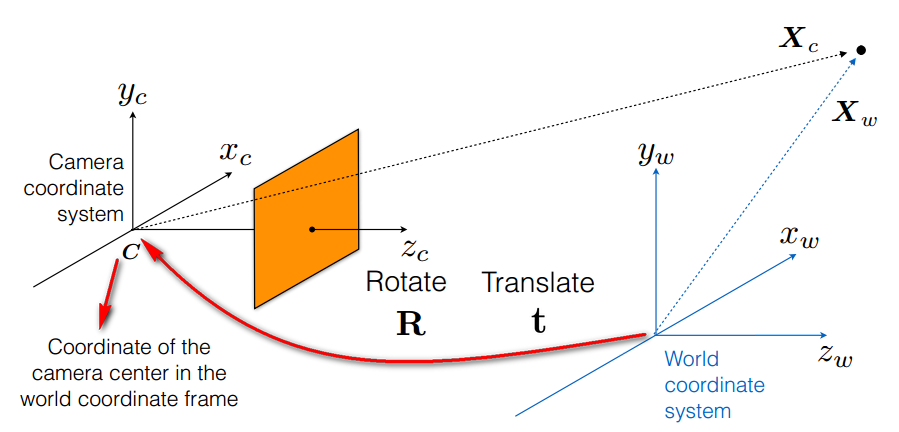
小白：這個R，t就是之前我們講過的變換矩陣吧
師兄：對啊，如果用數學公式表示的話，就是下面這個啦，我們在《從零開始一起學習SLAM | 為什麼要用齊次座標？》還講了為什麼要使用齊次座標，還記得吧？

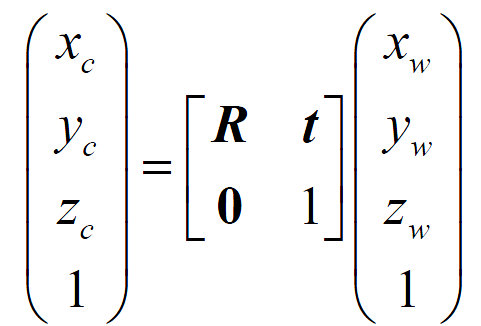
小白：記得呢，我有複習過的哦（頓時感覺自己也沒有那麼小白了），嘻嘻
師兄：不錯。這個R,t 為就是相機的外部引數，一般用T表示，這個引數隨著相機的移動而變化。下面我們假設已經把世界座標系變換到相機座標系下了。
我們再來說一下影象座標系(image coordinate system)吧，它是為了描述成像過程中物體從相機座標系到影象座標系的投影透射關係而引入，是我們真正從相機內讀取到的影象所在的座標系。單位為畫素。

針孔相機成像原理
我們來看看下面這個圖吧。相機座標系下的點P(X, Y, Z)在相機成像平面上成的像為P’(X’, Y’, Z’)

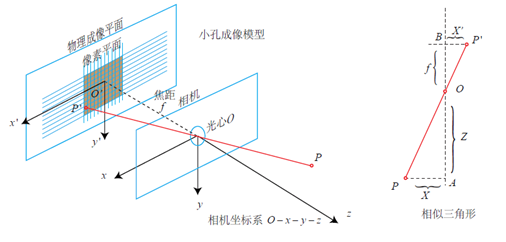
那麼根據三角形相似原理，如右圖所示，能推匯出如下式子

其中，f是相機的焦距。
小白：嗯，這個三角形相似還有印象，這個式子看懂了
師兄：但是成像過程一般是以影象中心點為座標系原點的，如下圖所示。而我們做影象處理的時候習慣於從左上角為影象座標系原點，所以。

小白：所以還需要一個平移？

師兄：恭喜，你都會搶答啦！下面式子中cx, cy就是分別在x,y方向的平移，一般是長和寬的一半。

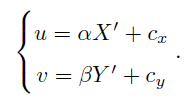
小白：師兄，好好的為什麼要平移啊？
師兄：哦，這是因為雖然成像的時候是以影象中心為原點，但是我們影象儲存的時候都是從左上角開始儲存的，這樣方便資料的讀寫
小白：原來是這樣啊！除了平移外，還有個尺度因子α，β，這個尺度因子從哪裡冒出來的？！
師兄：你想想，前面X’, Y’單位是什麼？cx, cy單位是什麼？
小白：X’, Y’單位應該和X,Y 類似，是（毫）米吧，cx, cy是影象座標系的，我們一般說影象多少多少畫素，那單位應該是畫素吧？
師兄：沒錯！所以需要尺度因子統一一下單位，所以尺度因子α，β單位是畫素/（毫）米，這樣和X’,Y’相乘後單位就是畫素啦！
小白：是哦，這樣就可以直接和cx, cy相加啦！等我默唸一般哈：

X’, Y’單位是 毫米
α，β單位是畫素/（毫）米
cx, cy單位是畫素

好啦，師兄繼續吧~
師兄：有了前面兩個式子，我們把第2個帶入第1個，就得到了下面式子，u, v都是影象座標系下座標，單位是畫素

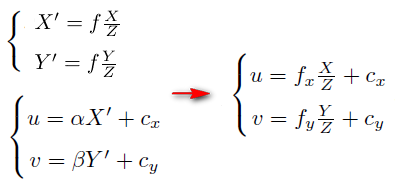
小白：這個公式看懂啦！不過我看書上都寫成矩陣的樣子了啊
師兄：沒錯，一般都寫成齊次座標，用矩陣表示，如下圖

左側影象座標是齊次座標，中間紅色框內的矩陣K稱為內參數，最右側藍色框內的就是相機座標系下的三維點P啦！
小白：寫成矩陣形式真的挺方便的！
師兄：對，你看還有一個1/Z 的係數，這個Z是相機座標系下P點的Z座標，如果把這個 1/Z 和 P(X,Y,Z) 進行相乘，就得到了相機座標系下P的歸一化座標 P = (X/Z, Y/Z, 1)， 它位於相機前方z =1 的平面上。
小白：原來這就是歸一化座標說法的來源啊！
師兄：對，我們結合前面從世界座標系到相機座標系的變換，就有了如下式子：

其中 fx, fy 分別是x, y方向焦距，一般都是相等的, cx,cy是光心位置，一般是長和寬的一半，他們都叫內參，此外還有畸變係數也屬於內參，他們都是相機固有引數。
到此，針孔相機成像模型就講完啦！
小白：嗯，感覺很有收穫！

師兄：總結一下整個過程：
1、首先，世界座標系下有一個三維點Pw
2、若世界座標系到相機座標系下的變換為旋轉矩陣 R 和平移向量t 組成的變換矩陣 T，那麼Pw在相機座標系下的座標為 Pc = RPw + t = TPw
3、此時的Pc三個分量分別是X, Y, Z，我們需要把它投影到歸一化平面Z=1上，這樣我們得到了相機座標系下Pc的歸一化座標 Pc’ = (X/Z, Y/Z, 1)
4、用內參矩陣乘以歸一化座標就得到了畫素座標 Puv = K*Pc’

小白：嗯，這下徹底明白啦！

相機畸變
小白：師兄，那個畸變引數還沒講呢！
師兄：哦對，這個畸變引數也很重要的，也是內參的重要組成。
小白：師兄，為啥相機會畸變啊？
師兄：這是因為我們的相機前面有個透鏡，如果想要相機一次性拍攝很大的範圍，像下面這個圖這樣，就需要把透鏡做的中間很厚兩邊薄，這樣光線經過透鏡後會發生折射，相機就能看到更多物體啦。不過這樣的話，我們前面的針孔模型中的那些三角形相似的假設就不能滿足啦！

也就是說：畸變產生的原因是：透鏡不能完全滿足針孔模型假設
小白：嗯，好像是這樣，那種魚眼相機看起來就是凸的很呢，拍出來圖片邊緣的房子都扭曲了。是不是所有相機都是一種型別的畸變啊？
師兄：不是的，相機透鏡的畸變主要分為徑向畸變和切向畸變，還有其他的畸變，但都沒有徑向和切向畸變影響顯著，所以我們在這裡只考慮徑向和切向畸變。
小白：啥是徑向啥是切向啊？
師兄：你看下面這個圖，很形象。這是徑向畸變的兩種型別，一種是桶形，像個木桶，一種是枕形，像個枕頭

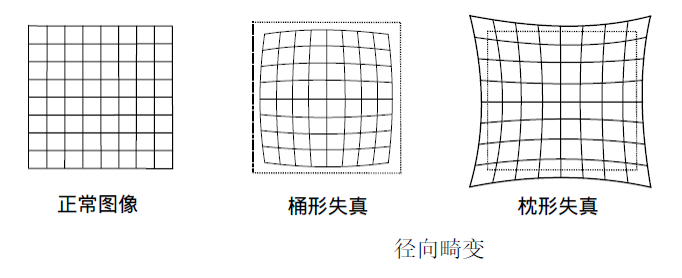
小白：真的很像哎，哈哈
師兄：你看他們的畸變程度有什麼特點？
小白：好像中間部分還好，越往周圍扭曲越嚴重？
師兄：是，畸變程度都是從中心開始，用一個半徑畫圓的話，半徑越大，圓周上的畸變程度也越大。這個就是由於相機透鏡的形狀導致的，且越向透鏡邊緣移動徑向畸變越嚴重。
小白：嗯，挺直觀的，那切向畸變是啥？
師兄：切向畸變是由於透鏡和CMOS或者CCD的安裝位置誤差導致。看下面的圖，因此，如果存在切向畸變，一個矩形被投影到成像平面上時，很可能會變成一個梯形。不過隨著相機制造工藝的大大提升，這種情況很少出現了，我們一般也不考慮切向的畸變。

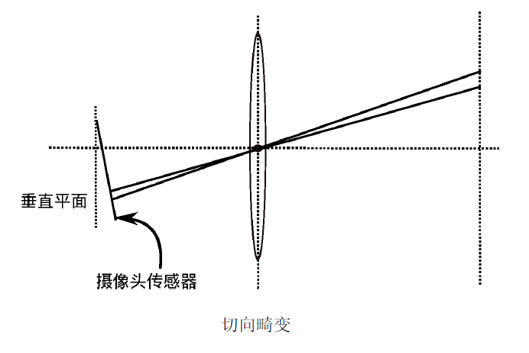
小白：那就是說只要考慮徑向畸變就行了？（不用學切向畸變了，yeah！）
師兄：對。下面我們來說說怎麼樣對畸變進行去除
小白：感覺很難的樣子。。。
師兄：是有點麻煩。首先需要對相機進行標定，標定完就能得到相機的所有內參，包括畸變係數。我們用標定的畸變係數就能對畸變的影象進行去畸變啦
小白：那這個相機標定怎麼做的？
師兄：這個還是挺複雜的，標定的原理你可以看看一個叫“計算機視覺life”的公眾號，裡面講相機標定原理還是挺清楚的~
小白：嗯，師兄，記住啦，我去關注一下。
師兄：假設我們已經標定好了，下面來看看如何用畸變係數來去畸變吧
小白：好啊，這個感覺很神奇啊
師兄：對，你看下面式子就是去畸變的公式，記住這個就行了。你看等式左邊都是拍攝的原圖的座標，就是發生了畸變的。

小白：下標的distorted出賣了它，哈哈
師兄：嗯，等式右邊的座標x, y是去畸變後的影象座標，它是歸一化的座標，以影象中心為原點，還有那個r 就是半徑啦，你看這是一個圓的方程。你覺得這個怎麼計算出 x, y？
小白：感覺這個計算好像很麻煩啊，左邊是已知，右邊是未知，再帶進去那個半徑，天吶，沒法想象啊！
師兄：確實如你所說，如果是正常的思維方式，確實很難解。不過，我們可以反過來算，就簡單多了
小白：怎麼反過來？
師兄：就是我們假設已經有了去畸變的影象了，對應下面左圖，它的座標 x, y自然已經知道了，然後帶入右邊式子，最後得到一個x_distorted, y_distorted的座標，這個座標對應的就是扭曲的圖裡的座標，就是下面右圖，我們只要把這個畫素值替換掉去畸變的圖片裡的 x, y 處畫素值就好啦！
小白：這個好神奇哦
師兄：嗯，很巧妙的方法。不過計算得到的 x_distorted, y_distorted可能不是整數，是一個浮點數，這就需要進行插值計算了。

小白：具體怎麼做呢？感覺還是有點暈呢
師兄：這個就是留給你的作業了，你自己做一遍，就不暈啦！
小白：（我暈。。）
作業
題目：相機視場角比較小（比如手機攝像頭）時，一般可以近似為針孔相機成像，三維世界中的直線成像也是直線。 但是很多時候需要用到廣角甚至魚眼相機，此時會產生畸變，三維世界中的直線在影象裡會彎曲。因此，需要做去畸變。 本題給定一張廣角畸變影象，以及相機的內參，請完成影象去畸變過程。已經給出程式碼框架及去畸變前後對比圖。具體獲得方法見下：

師兄提醒：關注“計算機視覺life”微信公眾號，選單欄回覆“畸變”，就能下載程式碼框架和圖片啦！
原文連結：從零開始一起學習SLAM | 相機成像模型

相關閱讀
從零開始一起學習SLAM | 為什麼要學SLAM？
從零開始一起學習SLAM | 學習SLAM到底需要學什麼？
從零開始一起學習SLAM | SLAM有什麼用？
從零開始一起學習SLAM | C++新特性要不要學？
從零開始一起學習SLAM | 為什麼要用齊次座標？
從零開始一起學習SLAM | 三維空間剛體的旋轉
從零開始一起學習SLAM | 為啥需要李群與李代數？
零基礎小白，如何入門計算機視覺？

---------------------
作者：electech6
來源：CSDN
原文：https://blog.csdn.net/electech6/article/details/83617892
版權宣告：本文為博主原創文章，轉載請附上博文連結！