這篇部落格是對極客時間上王爭課程 —— 資料結構與演算法之美的個人學習總結。文章中的圖出自課程中。我會對課程中的 Java 程式碼用 Python 來實現，所有的程式碼會放在我的 GitHub 上。

4. 歸併排序（Merge Sort）

歸併排序使用遞推的方式來實現，把需要排序的陣列逐步分成更小的部分，進行排序，然後再組合起來。由於是遞推，最重要的是要建立遞推公式：

看這裡的遞推公式：

遞推公式
merge_sort(p...r) = merge(merge_sort(p...q), merge_sort(q+1...r))

終止條件
p >= r 不用再繼續分解

 

遞推如果看程式碼去理解的話會很複雜，但是建立了遞推公式，按照公式來進行就會變得簡單很多。這個公式就是把陣列分為 p 到 q，q+1 到 r 兩部分，對每一部分都進行同樣的操作，直到不能再分。

按照遞推公式來弄成程式碼就是：

# Copyright(c) strongnine

## 歸併排序演算法, A 是陣列
def merge_sort(A):
    n = len(A)
    return merge_sort_c(A, 0, n - 1)

def merge_sort_c(A, p, r):
    ## 遞迴終止條件
    if p >= r:
        return
 


    ## 取 p 到 r 之間的中間位置 q
    q = (p + r) // 2
    ## 分治遞迴
    merge_sort_c(A, p, q)
    merge_sort_c(A, q+1, r)
    ## 將 A[p...q] 和 A[q+1...r] 合併為 A[p...r]
    A = merge(A, p, q, r)
    return A

def merge(A, p, q, r):
    i = p
    j = q + 1
    tmp = []
    while (i <= q) & (j <= r):
        if
 
 A[i] <= A[j]:
            tmp.append(A[i])
            i += 1
        else:
            tmp.append(A[j])
            j += 1


    ## 判斷哪個子陣列中有剩餘的資料
    start = i
    end = q
    if j <= r:
        start = j
        end = r
    ## 將剩餘的資料拷貝到臨時資料 tmp
    while start <= end:
        tmp.append(A[start])
        start += 1

    return tmp


if __name__ == '__main__':
    A = [1, 5, 6, 2, 3, 4]
    B = [1, 2, 3, 5, 7, 8, 9, 11]
    A = merge_sort(A)
    B = merge_sort(B)
    print(A, B)

其中最重要的就是 merge_sort_c() 這個函式，它有個巢狀。

歸併排序的過程分解如下：

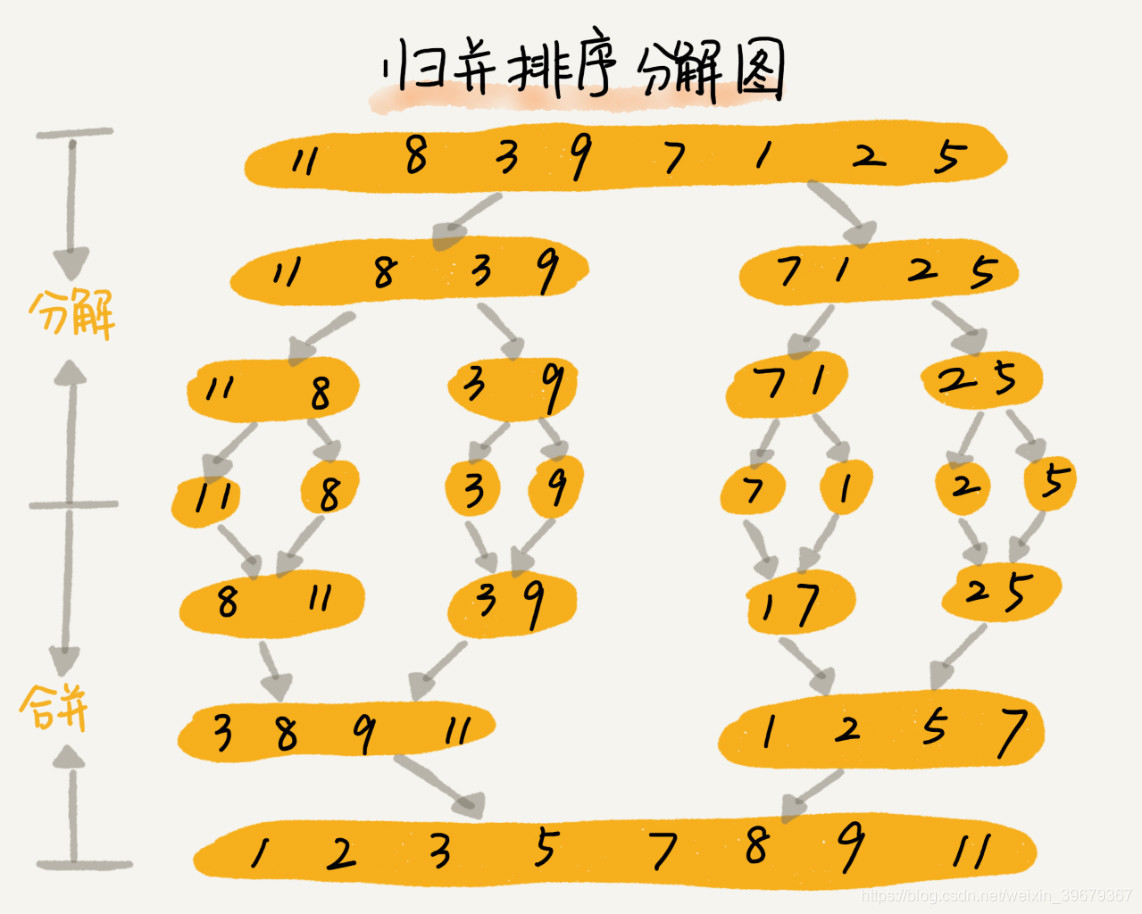
歸併排序是非原地的穩定的演算法，時間複雜度 O(nlogn)，空間複雜度 O(n)。

5. 快速排序（Quicksort）

快速排序簡稱快排，也是用的分治思想。遞推公式：

遞推公式：
quick_sort(p...r) = quick_sort(p...q-1) + quick_sort(q+1, r)

終止條件：
p >= r

程式碼：

# Copyright(c) strongnine

## 快速排序
def quick_sort(A):
    n = len(A)

    quick_sort_c(A, 0, n - 1)

    return A

def quick_sort_c(A, p, r):
    if p >= r:
        return

    ## 獲取分割槽點
    q = partition(A, p, r)
    quick_sort_c(A, p, q - 1)
    quick_sort_c(A, q + 1, r)

    return A

def partition(A, p, r):
    pivot = A[r]
    i = p
    for j in range(p, r):
        if A[j] < pivot:
            A[i], A[j] = A[j], A[i]
            i += 1

    A[i], A[r] = A[r], A[i]

    return i


if __name__ == '__main__':
    A = [11, 8, 3, 9, 7, 1, 2, 5]
    A = quick_sort(A)
    print(A)