因為最近一段時間接觸了一些Leetcode上的題目，發現許多題目的解題思路相似，從中其實可以瞭解某類演算法的一些應用場景。
這個隨筆系列就是我嘗試的分析總結，希望也能給大家一些啟發。

動態規劃的基本概念

一言以蔽之，動態規劃就是將大問題分成小問題，以迭代的方式求解。

可以使用動態規劃求解的問題一般有如下的兩個特徵：
1、有最優子結構（optimal substructure）
即待解決問題的最優解能夠通過求解子問題的最優解得到。

2、子問題間有重疊（overlapping subproplems）
即同樣的子問題在求解過程中會被多次呼叫，而不是在求解過程中不斷產生新的子問題。動態規劃一般會將子問題的解暫時存放在一個表中，以方便呼叫。（這也是動態規劃與分治法之間的區別）
下圖是斐波那契數列求解的結構圖，它並非是“樹狀”，也就是說明其子問題有重疊。

動態規劃的一般過程

1、分析得到結果的過程，發現子問題（子狀態）；

2、確定狀態轉移方程，即小的子問題與稍大一些的子問題間是如何轉化的。

以斐波那契為例（兩種方式：自頂向下與自底向上）

以求解斐波那契數列為例，我們很容易得到求解第N項的值的子問題是第i項（i＜N）的值。
而狀態轉移方程也顯而易見：f(n) = f(n-1) + f(n-2)

由此我們可以得到相應迭代演算法表達：

function fib()
    if n <= 1 return n
   return fib(n - 1) + fib(n - 2)

不過，如之前所說，動態規劃一個特點就是會儲存子問題的結果以避免重複計算，（我們將這種方式稱作

var m := map(0 -> 0, 1 -> 1)
function fib(n)
    if key n is not in map m
        m[n] := fib(n - 1) + fib(n - 2)
   return m[n]

上面的方式是自頂向下（Top-down）方式的，因為我們先將大問題“分為”子問題，再求解/存值；
而在自底向上（Bottom-up）方式中，我們先求解子問題，再在子問題的基礎上搭建出較大的問題。（或者，可以視為“迭代”(iterative)求解）通過這種方法的空間複雜度為O(1)

function fib(n)
    if n = 0
        return 0
   else
        var previousFib := 0, currentFib := 1
         repeat n - 1 times
            var newFib := previousFib + currentFib
            previousFib := currentFib
            currentFib  := newFib
    return currentFib

動態規劃與其他演算法的比較

動態規劃與分治法

分治法（Divide and Conquer）的思想是：將大問題分成若干小問題，每個小問題之間沒有關係，再遞迴的求解每個小問題，比如排序演算法中的“歸併排序”和“快速排序”；

而動態規劃中的不同子問題存在一定聯絡，會有重疊的子問題。因此動態規劃中已求解的子問題會被儲存起來，避免重複求解。

動態規劃與貪心演算法

貪心演算法（greedy algorithm）無需求解所有的子問題，其目標是尋找到區域性的最優解，並希望可以通過“每一步的最優”得到整體的最優解。

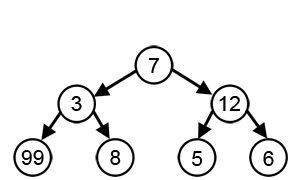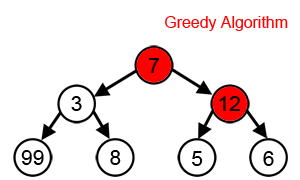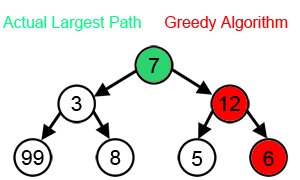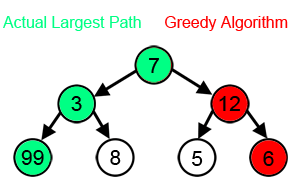
如果把問題的求解看作一個樹狀結構，動態規劃會考慮到樹中的每一個節點，是可回溯的；而貪心演算法只能在每一步的層面上做出最優判斷，“一條路走到黑”，是“一維”的。因此貪心演算法可以看作是動態規劃的一個特例。

那麼有沒有“一條路走到黑”，最後的結果也是最優解的呢？
當然有，比如求解圖的單源最短路徑用到的Dijkstra演算法就是“貪心”的：每一次都選擇最短的路徑加入集合。而最後得到的結果也是最優的。（這和路徑問題的特殊性質也有關係，因為如果路徑的權值非零，很容易就能得到路徑遞迴的結果“單增”）

Leetcode例題分析

Unique Binary Search Trees （Bottom-up）

96. Unique Binary Search Trees
Given n, how many structurally unique BST's (binary search trees) that store values 1 ... n?
給定n，求節點數為n的排序二叉樹（BST）共有幾種（無重複節點）。

思路

可以令根節點依次為節點1~n，比根節點小的組成左枝，比根節點大的組成右枝。
子樹亦可根據此方法向下分枝。遞迴求解。

演算法

令G(n)為長度為n的不同排序樹的數目（即目標函式）；
令F(i,n)為當根節點為節點i時，長度n的不同排序樹的數目。

對於每一個以節點i為根節點的樹，F(i,n)實際上等於其左子樹的G(nr)乘以其右子樹的G(nl);
因為這相當於在兩個獨立集合中各取一個進行排列組合，其結果為兩個集合的笛卡爾乘積

我們由此可以得到公式F(i,n) = G(i-1)*G(n-i)
從而得到G(n)的遞迴公式：
G(n) = ΣG(i-1)G(n-i)

演算法實現

class Solution {
    public int numTrees(int n) {
        int[] G = new int[n+1];
        G[0] = 1;
        G[1] = 1;

        for(int i = 2; i <= n; ++i){
            for(int j = 1; j <= i; ++j){
                G[i] += G[j - 1] * G[i - j];
            }
        }
        return G[n];
    }
}

一個典型的“自底向上”的動態規劃問題。
當然，由於通過遞推公式可以由數學方法得到G(n)的計算公式，直接使用公式求解也不失為一種方法。

Coin Change （Top-down）

322. Coin Change
You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.
coins陣列表示每種硬幣的面值，amount表示錢的總數，若可以用這些硬幣可以組合出給定的錢數，則返回需要的最少硬幣數。無法組合出給定錢數則返回-1。

演算法思路

1、首先定義一個函式F(S) 對於amount S 所需要的最小coin數
2、將問題分解為子問題：假設最後一個coin面值為C 則F(S) = F(S - C) + 1
S - ci >= 0 時，設F(S) = min[F(S - ci)] + 1 (選擇子函式值最小的子函式，回溯可得到總體coin最少)
S == 0 時，F(S) = 0;
n == 0 時，F(S) = -1

演算法實現

class Solution {
    public int coinChange(int[] coins, int amount) {
        if(amount < 1) return 0;
        return coinChange(coins, amount, new int[amount]);
    }

    private int coinChange(int[] coins, int rem, int[] count)
    {
        if(rem < 0) return -1; 
        if(rem == 0) return 0;
        if(count[rem - 1]!=0) return count[rem - 1]; //這裡的rem-1 其實就相當於 rem 從 0 開始計數(不浪費陣列空間)
        int min = Integer.MAX_VALUE; //每次遞迴都初始化min
        for(int coin : coins){
            int res = coinChange(coins, rem - coin, count); //計運算元樹值
            if(res >= 0 && res < min) 
                min = 1 + res; //父節點值 = 子節點值+1 （這裡遍歷每一種coin之後得到的最小的子樹值）
        }
        count[rem - 1] = (min == Integer.MAX_VALUE) ? -1:min; //最小值存在count[rem-1]裡，即這個數值(rem)的最小錢幣數確定了
        return count[rem-1];
    }
}

演算法採用了動態規劃的“自頂向下”的方式，使用了回溯法(backtracking)，並且對於回溯樹進行剪枝（coin面值大於amount時）。
同時，為了降低時間複雜度，將已計算的結果（一定面值所需要的最少coin數）儲存在對映表中。

雖然動態規劃是錢幣問題的一般認為的解決方案，然而實際上，大部分的貨幣體系（比如美元/歐元）都是可以通過“貪心演算法”就能得到最優解的。

最後，如果大家對於文章有任何意見/建議/想法，歡迎留言討論！