數字三角形案例

題目描述 Description

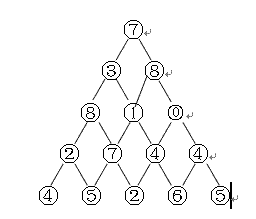
下圖給出了一個數字三角形，請編寫一個程式，計算從頂至底的某處的一條路徑，使該路徑所經過的數字的總和最大。
（1）每一步可沿左斜線向下或右斜線向下
（2）1 < 三角形行數 < 100
（3）三角形數字為0，1，…99

輸入描述 Input Description

有很多個測試案例，對於每一個測試案例， 通過鍵盤逐行輸入，第1行是輸入整數（如果該整數是0,就表示結束，不需要再處理），表示三角形行數n，然後是n行數

輸出描述 Output Description

輸出最大值。

樣例輸入 Sample Input

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

樣例輸出 Sample Output

30

遞迴解法

解題思路

用二維陣列存放數字三角形。
D( r, j) : 第r行第 j 個數字(r,j從1 開始算)
MaxSum(r, j) : 從D(r,j)到底邊的各條路徑中，最佳路徑的數字之和。
問題：求 MaxSum(1,1)
典型的遞迴問題。
D(r, j)出發，下一步只能走D(r+1,j)或者D(r+1, j+1)。故對於N行的三角形：

if ( r == N)
 MaxSum(r,j) = D(r,j)
else
 

 MaxSum( r, j) = Max{ MaxSum(r＋1,j), MaxSum(r+1,j+1) } + D(r,j)

程式碼實現

#include <iostream>
#include <algorithm>

#define Max 101

using namespace std;

int D[Max][Max];

int num;

int MaxSum(int i, int j){
    if(i == num)
        return D[i][j];
    int x = MaxSum(i + 1, j);
    int
 
 y = MaxSum(i + 1, j + 1);
    return max(x,y) + D[i][j];
}

int main(int argc, char const *argv[])
{
    int i, j;

    cin >> num;

    for(i = 1; i <= num; i ++)
        for(j = 1; j <= i; j ++)
            cin >> D[i][j];
    cout << MaxSum(1,1) << endl;
    return 0;
}

時間複雜度

遞迴求解，會嚴重超時，因為出現重複計算，如下圖所示。深度遍歷每條路徑，存在大量重複計算。5行的總時間為：1+2+4+8+16=31=25−1則時間複雜度為 2n

記憶遞迴動歸程式

解題思路

第一次計算MaxSum(r,j)值的時候，儲存下來，下次需要的時候，直接取出計算，這樣就避免了重複計算。時間複雜度為O(n2)，因為三角形的數字總和為n(n+1)/2。

程式碼實現

#include <iostream>
#include <algorithm>
#include "string.h"

#define Max 101

using namespace std;

int D[Max][Max];
int Max_Sum_arr[Max][Max];

int num;

int MaxSum(int i, int j){
    if(Max_Sum_arr[i][j] != -1)
        return Max_Sum_arr[i][j];
    if(i == num)
        Max_Sum_arr[i][j] = D[i][j];
    else{
        int x = MaxSum(i + 1, j);
        int y = MaxSum(i + 1, j + 1);
        Max_Sum_arr[i][j] = max(x,y) + D[i][j];
    }

    return Max_Sum_arr[i][j];
}

int main(int argc, char const *argv[])
{
    int i, j;

    cin >> num;

    for(i = 1; i <= num; i ++)
        for(j = 1; j <= i; j ++)
            cin >> D[i][j];
    memset(Max_Sum_arr,-1,sizeof(Max_Sum_arr));
    cout << MaxSum(1,1) << endl;
    return 0;
}

遞推型動歸程式

解題思路

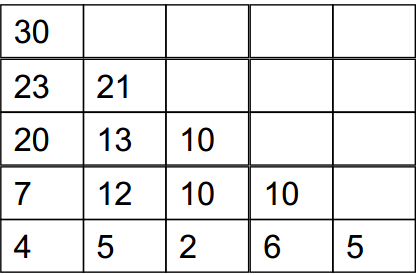
從底向上遞推，出最後一行外，每一行的每個點的最大值等於自身加上下面一行對應左右兩個點的最大值，從下往上遞推，最頂部的即所求。比如下圖所示。首先最後一行的最大值就是它本身。倒數第二行第一個數7就是輸入的倒二行的第一個數2 + 4 和 2 +5 取最大值 。逐步遞推到頂部。

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

程式碼實現

#include <iostream>
#include <algorithm>
#include "string.h"

#define Max 101

using namespace std;

int D[Max][Max];


int num;



int MaxSum(int num){
    int i, j;
    for(i = num - 1; i >= 1; i --)
        for(j = 1; j <= i; j ++){
            D[i][j] = max(D[i+1][j],D[i+1][j+1]) + D[i][j];
        }
    return D[1][1];
}
int main(int argc, char const *argv[])
{
    int i, j;

    cin >> num;

    for(i = 1; i <= num; i ++)
        for(j = 1; j <= i; j ++)
            cin >> D[i][j];
    cout << MaxSum(num) << endl;
    return 0;
}

動規解題的一般思路

1、將原問題分解為子問題

• 把原問題分解為若干個子問題，子問題和原問題形式相同或類似，只不過規模變小了。子問題都解決，原問題即解決(數字三角形例）
• 子問題的解一旦求出就會被儲存，所以每個子問題只需求解一次。

2、確定狀態

在用動態規劃解題時，我們往往將和子問題相關的各個變數的一組取值，稱之為一個“狀態”。一個“狀態”對應於一個或多個子問題，所謂某個“狀態”下的“值”，就是這個“狀態”所對應的子問題的解。

3、確定一些初始狀態（邊界狀態）的值

以“數字三角形”為例，初始狀態就是底邊數字，值就是底邊數字值。

4、確定狀態轉移方程

定義出什麼是“狀態”，以及在該 “狀態”下的“值”後，就要找出不同的狀態之間如何遷移――即如何從一個或多個“值”已知的“狀態”，求出另一個“狀態”的“值” 。狀態的遷移可以用遞推公式表示，此遞推公式也可被稱作“狀態轉移方程”。

能用動規解決的問題的特點

1. 問題具有最優子結構性質。如果問題的最優解所包含的子問題的解也是最優的，我們就稱該問題具有最優子結構性質。
2. 無後效性。當前的若干個狀態值一旦確定，則此後過程的演變就只和這若干個狀態的值有關，和之前是採取哪種手段或經過哪條路徑演變到當前的這若干個狀態，沒有關係。

參考資料

《程式設計導引及線上實踐》——北京大學資訊科學技術學院