2. 程式人生 > >影象質量評價相關收錄

影象質量評價相關收錄

阿新 • • 發佈：2018-12-05

2018-12-05 轉自 ：https://www.cnblogs.com/ranjiewen/p/6390846.html#undefined 

ssim的計算裡面有高斯模糊

為了快速計算，先對每個小塊進行計算，然後計算所有塊的平均值。

可以參考原始碼實現，而且程式碼實現有近似的在裡面！matlab中中影象PSNR和SSIM的計算

“在實際應用中，可以利用滑動窗將影象分塊，令分塊總數為N，考慮到視窗形狀對分塊的影響，採用高斯加權計算每一視窗的均值、方差以及協方差，然後計算對應塊的結構相似度SSIM，最後將平均值作為兩影象的結構相似性度量，即平均結構相似性MSSIM”

function [mssim, ssim_map] = ssim(img1, img2, K, window, L)

 
 
% ========================================================================
% SSIM Index with automatic downsampling, Version 1.0
% Copyright(c) 2009 Zhou Wang
% All Rights Reserved.
%
% ----------------------------------------------------------------------
% Permission to use, copy, or modify this software and its documentation
% for educational and research purposes only and without fee is hereby
% granted, provided that this copyright notice and the original authors'
% names appear on all copies and supporting documentation. This program
% shall not be used, rewritten, or adapted as the basis of a commercial
% software or hardware product without first obtaining permission of the
% authors. The authors make no representations about the suitability of
% this software for any purpose. It is provided "as is" without express
% or implied warranty.
%----------------------------------------------------------------------
%
% This is an implementation of the algorithm for calculating the
% Structural SIMilarity (SSIM) index between two images
%
% Please refer to the following paper and the website with suggested usage
%
% Z. Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli, "Image
% quality assessment: From error visibility to structural similarity,"
% IEEE Transactios on Image Processing, vol. 13, no. 4, pp. 600-612,
% Apr. 2004.
%
% http://www.ece.uwaterloo.ca/~z70wang/research/ssim/
%
% Note: This program is different from ssim_index.m, where no automatic
% downsampling is performed. (downsampling was done in the above paper
% and was described as suggested usage in the above website.)
%
% Kindly report any suggestions or corrections to 
 
[email protected]
%
%----------------------------------------------------------------------
%
%Input : (1) img1: the first image being compared
% (2) img2: the second image being compared
% (3) K: constants in the SSIM index formula (see the above
% reference). defualt value: K = [0.01 0.03]
% (4) window: local window for statistics (see the above
% reference). default widnow is Gaussian given by
% window = fspecial('gaussian', 11, 1.5);
% (5) L: dynamic range of the images. default: L = 255
%
%Output: (1) mssim: the mean SSIM index value between 2 images.
% If one of the images being compared is regarded as 
% perfect quality, then mssim can be considered as the
% quality measure of the other image.
% If img1 = img2, then mssim = 1.
% (2) ssim_map: the SSIM index map of the test image. The map
% has a smaller size than the input images. The actual size
% depends on the window size and the downsampling factor.
%
%Basic Usage:
% Given 2 test images img1 and img2, whose dynamic range is 0-255
%
% [mssim, ssim_map] = ssim(img1, img2);
%
%Advanced Usage:
% User defined parameters. For example
%
% K = [0.05 0.05];
% window = ones(8);
% L = 100;
% [mssim, ssim_map] = ssim(img1, img2, K, window, L);
%
%Visualize the results:
%
% mssim %Gives the mssim value
% imshow(max(0, ssim_map).^4) %Shows the SSIM index map
%========================================================================
 
 
 
 
 

if (nargin < 2 || nargin > 5)
 mssim = -Inf;
 ssim_map = -Inf;
 return;
end
 
 
 
 
if (size(img1) ~= size(img2))
 mssim = -Inf;
 ssim_map = -Inf;
 return;
end
 
 
 
 
[M,N] = size(img1);
 
 
 
 
if (nargin == 2)
 if ((M < 11) || (N < 11)) %影象尺寸大小太小 沒有意義
 mssim = -Inf;
 ssim_map = -Inf;
 return
 end
 window = fspecial('gaussian', 11, 1.5); %標準偏差為1.5 ， 11*11的高斯低通濾波器
 K(1) = 0.01; % default settings
 K(2) = 0.03; %
 L = 255; %
end
 
 
 
 
if (nargin == 3)
 if ((M < 11) || (N < 11))
 mssim = -Inf;
 ssim_map = -Inf;
 return
 end
 window = fspecial('gaussian', 11, 1.5);
 L = 255;
 if (length(K) == 2)
 if (K(1) < 0 || K(2) < 0)
 mssim = -Inf;
 ssim_map = -Inf;
 return;
 end
 else
 mssim = -Inf;
 ssim_map = -Inf;
 return;
 end
end
 
 
 
 
if (nargin == 4)
 [H,W] = size(window);
 if ((H*W) < 4 || (H > M) || (W > N))
 mssim = -Inf;
 ssim_map = -Inf;
 return
 end
 L = 255;
 if (length(K) == 2)
 if (K(1) < 0 || K(2) < 0)
 mssim = -Inf;
 ssim_map = -Inf;
 return;
 end
 else
 mssim = -Inf;
 ssim_map = -Inf;
 return;
 end
end
 
 
 
 
if (nargin == 5)
 [H,W] = size(window);
 if ((H*W) < 4 || (H > M) || (W > N))
 mssim = -Inf;
 ssim_map = -Inf;
 return
 end
 if (length(K) == 2)
 if (K(1) < 0 || K(2) < 0)
 mssim = -Inf;
 ssim_map = -Inf;
 return;
 end
 else
 mssim = -Inf;
 ssim_map = -Inf;
 return;
 end
end
 
 
 
 

img1 = double(img1);
img2 = double(img2);
 
 
 
 
% automatic downsampling
f = max(1,round(min(M,N)/256));
%downsampling by f
%use a simple low-pass filter 
if(f>1)
 lpf = ones(f,f);
 lpf = lpf/sum(lpf(:));
 img1 = imfilter(img1,lpf,'symmetric','same');
 img2 = imfilter(img2,lpf,'symmetric','same');
 
 
 
 
 img1 = img1(1:f:end,1:f:end);
 img2 = img2(1:f:end,1:f:end);
end
 
 
 
 
C1 = (K(1)*L)^2;
C2 = (K(2)*L)^2;
window = window/sum(sum(window));
 
 
 
 
mu1 = filter2(window, img1, 'valid');
mu2 = filter2(window, img2, 'valid');
mu1_sq = mu1.*mu1;
mu2_sq = mu2.*mu2;
mu1_mu2 = mu1.*mu2;
sigma1_sq = filter2(window, img1.*img1, 'valid') - mu1_sq;
sigma2_sq = filter2(window, img2.*img2, 'valid') - mu2_sq;
sigma12 = filter2(window, img1.*img2, 'valid') - mu1_mu2;
 
 
 
 
if (C1 > 0 && C2 > 0)
 ssim_map = ((2*mu1_mu2 + C1).*(2*sigma12 + C2))./((mu1_sq + mu2_sq + C1).*(sigma1_sq + sigma2_sq + C2));
else
 numerator1 = 2*mu1_mu2 + C1;
 numerator2 = 2*sigma12 + C2;
 denominator1 = mu1_sq + mu2_sq + C1;
 denominator2 = sigma1_sq + sigma2_sq + C2;
 ssim_map = ones(size(mu1));
 index = (denominator1.*denominator2 > 0);
 ssim_map(index) = (numerator1(index).*numerator2(index))./(denominator1(index).*denominator2(index));
 index = (denominator1 ~= 0) & (denominator2 == 0);
 ssim_map(index) = numerator1(index)./denominator1(index);
end
 
 
 
 
mssim = mean2(ssim_map);
 
 
 
 
return
 
 
 
 
 

PSNR , 峰值信噪比
 

通常用來評價一幅影象壓縮後和原影象相比質量的好壞，當然，壓縮後圖像一定會比原影象質量差的，所以就用這樣一個評價指標來規定標準了。PSNR越高，壓縮後失真越小。這裡主要定義了兩個值，一個是均方差MSE，另一個是峰值信噪比PSNR，公式如下：
 

 

 

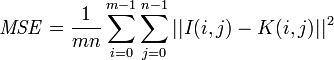
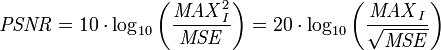
PSNR越高，影象和原圖越接近。當然，這都是客觀指標，實際評價還有主觀指標，不過主觀的東西就比較模糊了，每個人感覺都會不同的。最常用的全參考視訊質量評價方法有以下2種：
 

PSNR（峰值信噪比）：用得最多，但是其值不能很好地反映人眼主觀感受。一般取值範圍：20-40.值越大，視訊質量越好。
 

SSIM（結構相似性）：計算稍複雜，其值可以較好地反映人眼主觀感受。一般取值範圍：0-1.值越大，視訊質量越好。
 

PSNR，SSIM計算有如下工具可選：
 

MSU Video Quality Measurement Tool：商業軟體，圖形化介面，易上手，使用有限制。
 

Evalvid中的psnr.exe：開源軟體，命令列介面，使用無限制。推薦，適合批處理。
 
 

注：MOS（Mean Opnion Score，平均意見分）是主觀評價實驗之後，得到的主觀分數，取值0-100，值越大，代表主觀感受越好。以下實驗資料來自Live資料庫：http://live.ece.utexas.edu/research/Quality/
 

 SSIM引數
 

         一種衡量兩幅影象相似度的新指標，其值越大越好，最大為1，經常用到影象處理中，特別在
 影象去噪處理中在影象相似度評價上全面超越SNR（signal to noise ratio）和PSNR（peak signal to noise ratio）。
 

 結構相似性理論認為，自然影象訊號是高度結構化的，即畫素間有很強的相關性，特別是空域中最接近的畫素，這種相關性蘊含著視覺場景中物體結構的重要資訊；
 

 HVS的主要功能是從視野中提取結構資訊，可以用對結構資訊的度量作為影象感知質量的近似。結構相似性理論是一種不同於以往模擬HVS低階的組成結構的全新思想，與基於HVS特性的方法相比，最大的區別是自頂向下與自底向上的區別。這一新思想的關鍵是從對感知
 誤差度量到對感知結構失真度量的轉變。它沒有試圖通過累加與心理物理學簡單認知模式有關的誤差來估計影象質量，而是直接估計兩個複雜結構訊號的結構改變，從而在某種程度上繞開了自然影象內容複雜性及多通道去相關的問題。作為結構相似性理論的實現，結構相似度指數從影象組成的角度將結構資訊定義為獨立於
 亮度、
 對比度的，反映場景中物體結構的屬性，並將失真建模為亮度、對比度和結構三個不同因素的組合。用
 均值作為亮度的估計，標準差作為
 對比度的估計，
 協方差作為結構相似程度的度量。
 

  
 

         結構相似性指標(英文：
 structural similarity index，
 SSIM index)是一種用以衡量兩張
 數位影像相似程度的指標。當兩張影像其中一張為無
 失真影像，另一張為
 失真後的影像，二者的結構相似性可以看成是失真影像的影像品質衡量指標。相較於傳統所使用的影像品質衡量指標，像是
 峰值信噪比(英文：
 PSNR)，結構相似性在影像品質的衡量上更能符合人眼對影像品質的判斷。
 

  
 
 
 
實際使用時，簡化起見，一般會將引數設為\alpha=\beta=\gamma=1及C_3=C_2/2，得到：
 
 
\text{SSIM}(\mathbf{x},\mathbf{y})=\frac{(2\mu_x\mu_y+C_1)(2\sigma_{xy}+C_2)}{(\mu_x^2+\mu_y^2+C_1)(\sigma_x^2+\sigma_y^2+C_2)}
 
 
        在計算兩張影像的結構相似性指標時，會開一個區域性性的視窗，一般為N×N的小區塊，計算出視窗內訊號的結構相似性指標，每次以畫素為單位移動視窗，直到整張影像每個位置的區域性結構相似性指標都計算完畢。將全部的區域性結構相似性指標平均起來即為兩張影像的結構相似性指標。
 
 
     
  
  • 在實際應用中，可以利用滑動窗將影象分塊，令分塊總數為N，考慮到視窗形狀對分塊的影響，採用高斯加權計算每一視窗的均值、方差以及協方差，然後計算對應塊的結構相似度SSIM，最後將平均值作為兩影象的結構相似性度量，即平均結構相似性MSSIM:
    •  
 
 
 
opencv和matlab都有現成的函式可以使用。
 
 
參考：影象質量評價--SSIM
 
 
         全參考視訊質量評價方法（PSNR，SSIM）以及相關資料庫
 
 
 影象質量評價指標
 
  
 
MSE: Mean Squared Error 
均方誤差是指引數估計值與引數真值之差平方的期望值; 
MSE可以評價資料的變化程度，MSE的值越小，說明預測模型描述實驗資料具有更好的精確度。
 
 
RMSE 
均方誤差:均方根誤差是均方誤差的算術平方根
 
 
MAE :Mean Absolute Error 
平均絕對誤差是絕對誤差的平均值 
平均絕對誤差能更好地反映預測值誤差的實際情況.
 
 
SD :standard Deviation 
標準差:標準差是方差的算術平方根。標準差能反映一個數據集的離散程度。平均數相同的兩組組資料，標準差未必相同。
 
  
  
  
          Spearman秩序相關係數（SROCC）本身就不是衡量線性相關的，而是衡量秩序的相關性的。設有兩組序列X和Y，其秩序為R(X)和R(Y)，這裡R(Xi)=k代表Xi是序列X中的第k大（或第k小），則SROCC(X, Y) = PLCC(R(X), R(Y))，其中PLCC是Pearson線性相關係數。
   
      SROCC被認為是最好的非線性相關指標，這是因為，SROCC只與序列中元素的排序有關。因此即使X或Y被任何單調非線性變換作用（如對數變換、指數變換），都不會對SROCC造成任何影響，因為不會影響元素的排序。維基百科有一張很直觀的圖片，很好地體現了SROCC與PLCC的區別。
   
  
 

 

 除此之外，還有一個Kendall秩序相關係數（KROCC），它的定義是pairwise的：
KROCC = (同序對數-逆序對數) / 總對數    （總對數=n(n - 1)/2）它的性質與SROCC類似，但是比較抖。
 

對於連續輸出的機器學習模型或簡單的迴歸擬合，發Paper的話，一般要放SROCC和PLCC，這兩個標準是最重要的，可以很好地衡量模型的非線性相關性和線性相關性。偶爾也會放KROCC和RMSE（方均根誤差）。但是SROCC是比PLCC更為根本的指標，因為一個複雜模型總可以用一些附加的非線性變換（對數或者指數，還有某些領域內recommanded複雜的組合= =）來補正，使得PLCC更高一些，而SROCC卻不能被這些附加非線性變換來影響。
 

 
   
 
 
 
 

            
  

           

              
              

            

            
相關推薦

			   
            
            
            
 

    


    
    
影象質量評價相關收錄

     
 2018-12-05 轉自 ：https://www.cnblogs.com/ranjiewen/p/6390846.html#undefined  
ssim的計算裡面有高斯模糊 
為了快速計算，先對每個小塊進行計算，然後計算所有塊的平均值。 
可以參考原始碼實現，而且程式碼實現有近似的在裡面！m 



  
 

    


    
    
影象質量評價指標之 PSNR 和 SSIM

     
 1. PSNR (Peak Signal-to-Noise Ratio) 峰值信噪比 
給定一個大小為 \(m×n\) 的乾淨影象 \(I\) 和噪聲影象 \(K\)，均方誤差 \((MSE)\) 定義為： 
\[MSE = \frac{1}{mn}\sum_{i=0}^{m-1}\sum_{j=0}^{n- 



  
 

    


    
    
經典影象質量評價指標原理

     
  
  
  
 有參評價指標 (1)均方誤差（MSE）和峰值信噪比（PSNR） 均方誤差（Mean Squared Error, MSE）通過取兩幅影象的均方差來計算“平均誤差”，是一種較方便簡單的影象質量評價方法，可以評價資料間的差異程度。 
 峰值信噪比（Peak Signal to Noise Rat 



  
 

    


    
    
影象質量評價之結構相似性SSIM（上）

     
 
							
							
							這篇文章主要介紹對影象質量進行打分評價的一個很經典的指數——結構相似性（structual similarity, SSIM）。
具體一點兒來說，影象在各種情況下都有可能失真，比如經過傳輸、壓縮和縮放等等。圖片變換之後，我們自然很想知道失真影象（distorte 



  
 

    


    
    
影象質量評價之結構相似性SSIM（中）

     
 
							
							
							在上一篇文章中，我們介紹了對影象質量進行評價的必要性、主觀評價和客觀評價的兩種標準，以及設計符合人類直覺的評價標準的困難性和重要性。
本來這篇文章想把我們的主角SSIM講完，但是發現前面需要寫的鋪墊有點長hhh，所以本文是作為一個過渡，系統的講解一下設計影象評價 



  
 

    


    
    
近期deep learning做影象質量評價（image quality assessment）的論文3

     
 
                
1、VeNICE: A very deep neural network approach to no-reference image assessment.

1.1框架：總共包括5個group，group1：conv，conv，relu，maxpool；group2：c 



  
 

    


    
    
兩種常用的全參考影象質量評價指標——峰值信噪比（PSNR）和結構相似性（SSIM）

     
 
                原文：https://blog.csdn.net/zjyruobing/article/details/49908979 

1.PSNR（Peak Signal to Noise Ratio）峰值信噪比：


MSE表示當前影象X和參考影象Y的均方誤差（Mean Squar 



  
 

    


    
    
無參考影象質量評價之影象質量評價方法（一）[均方根誤差、峰值信噪比、結構相似度]

     
 
								
								            
						
                
        影象質量評價在計算機視覺，人工智慧，高清視訊傳輸上面有很廣泛的應用。目前，影象質量評價主要分為三個方向，有參考影象的質量評價，半參考的影象質量評價，以及無參考的影象質量評價。但是，個人 



  
 

    


    
    
影象質量評價方法PSNR+SSIM&&評估指標SROCC,PLCC

     
 
                

ssim的計算裡面有高斯模糊，為了快速計算，先對每個小塊進行計算，然後計算所有塊的平均值。可以參考原始碼實現，而且程式碼實現有近似的在裡面！matlab中中影象PSNR和SSIM的計算

“在實際應用中，可以利用滑動窗將影象分塊，令分塊總數為N，考慮到視窗形狀對分塊的影響 



  
 

    


    
    
影象質量評價的方法和意義

     
 
                


在影象資訊科技被廣泛應用的情況下，對影象質量的評；比如，在影象識別中，所採集到的影象質量直接影響識；從有沒有人蔘與的角度區分，影象質量評價方法有主觀；影象質量的主觀評價；主觀評價只涉及人作出的定性評價，它以人為觀察者，；絕對評價；所謂絕對評價，是由觀察者根據自己的知識和 



  
 

    


    
    
無參考影象質量評價之基於多特徵的增強影象質量評價

     
 
								
								            
						
                
參考文獻

本節主要參考的文獻是：
Leida, Shen, Jinjian, et al. No-Reference Quality Assessment of Enhanced Images[J] 



  
 

    


    
    
人類視覺感知【4】立體影象的質量評價

     
 
                
        對於我的開題方向又有了新的想法，先是人類視覺感知，然後老師讓我做動畫壓縮的小方向，現在又要融合平行計算，我頭都大了！
       動畫，有二維動畫也有三維動畫，當然說到現在的動畫片已經不能單純的說是二維動畫還是以三維動畫，現在混合功能居多，但對於我的壓縮方 



  
 

    


    
    
影象濾波及質量評價

     
 
                
影象濾波
      
在影象處理中，消除影象中的噪聲成分叫作影象的平滑化或濾波操作。影象濾波起著重要作用，它可以有效地抑制和平滑各種噪聲、保持邊緣資訊，從而改善後續影象處理工作的質量，如提高影象分割精度等。
（1）濾波的原理在於：訊號或影象的能量大部分集中在幅度譜的低頻和 



  
 

    


    
    
全參考視訊質量評價方法（PSNR，SSIM）以及相關資料庫

     
 
                最常用的全參考視訊質量評價方法有以下2種：PSNR（峰值信噪比）：用得最多，但是其值不能很好地反映人眼主觀感受。一般取值範圍：20-40.值越大，視訊質量越好。SSIM（結構相似性）：計算稍複雜，其值可以較好地反映人眼主觀感受。一般取值範圍：0-1.值越大，視訊質量越好。PS 



  
 

    


    
    
簡練網軟考知識點整理-軟件質量保證及質量評價

     
 nag   ima   制造   相關   用戶   約束   適應性   使用   標準       軟件質量指的是軟件特性的總和，是軟件滿足用戶需求的能力，即遵從用戶需求，達到用戶滿意。    IS09126定義的軟件質量包括“內部質量”、“外部質量”和“使用質量”三部分。軟件滿足規定或潛在用戶需求的能力 



  
 

    


    
    
關於‘基於UML的教學質量評價系統建模研究’隨筆

     
 文獻   重要   學生   這才   解決   評價   想象   strong   變化   ?? 我認為關於教學質量評價最重要的就是調查過程中應該要有私密性，這才使調查具有真實性。在本校的這幾年中，本人也曾使用過教學質量評價系統，所以在看文獻之前我也有了對這個系統最基本的看法，那就是要設立兩個角色：學生 



  
 

    


    
    
文件拍攝技巧之拍照與如何提高影象質量

     
  
 
 有時候，掃描並不是獲取影象文件的唯一方法。在不具備掃描裝置的情況下，finereader同樣可以識別用相機或手機拍攝的文件照片。但是如何能讓拍攝的照片更易於識別呢？ 
  
 要獲取文件的較高質量的照片，請確保正確擺放相機的位置並遵循以下簡單的建議。 
 ●在可能情況下儘量使用三腳架。 
 ●盡頭位 



  
 

    


    
    
基於深度學習的影象質量排序

     
  
 
 國內外各大網際網路公司（比如騰訊、阿里和Yelp）的線上廣告業務都在關注展示什麼樣的影象能吸引更多點選。在美團，商家的首圖是由商家或運營人工指定的，如何選擇首圖才能更好地吸引使用者呢？影象質量排序演算法目標就是做到自動選擇更優質的首圖，以吸引使用者點選。 
 傳統的影象質量排序方法主要從美學角度進行 



  
 

    


    
    
語音質量評價

     
 1、影響語音質量的因素
     語音通訊系統中，影響語音質量的因素包括延時(delay)、丟包(packet loss)、包延遲變化(packet delay variation)、回聲(echo)、以及由於編碼造成的失真。將影響語音質量的因素分成三類，第一類是造成L 



  
 

    


    
    
像頭影象質量常用指標的測試方法

     
  
  
   
   像頭影象質量常用指標的測試方法 
   
   
   
    2017年11月28日 15:18:36 
    北絡 
    閱讀數：3829 
    標籤： 攝像頭除錯CameraISP 更多 
    
     個人分類