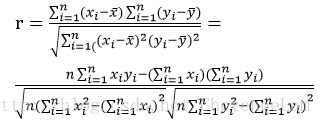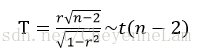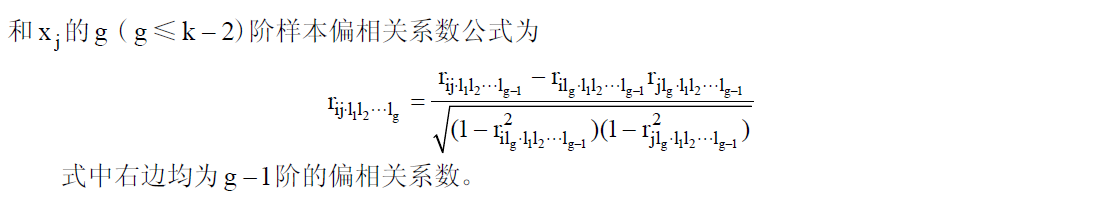R語言學習-第十課-相關分析
阿新 • • 發佈:2018-12-05
1.相關係數的估計和檢驗
相關係數作為隨機變數之間相關程度的度量指標,能刻畫線性關係的相關程度
對於二維隨機變數,相關係數的一個矩估計,也是樣本相關係數為
提出假設:
H0:總體A的相關係數ρ=0(也就是說假設總體上文盲率和預期壽命沒有相關關係)
H1:總體A的相關係數ρ≠0(也就是說總體上文盲率和預期壽命有相關關係)
計算檢驗的統計量:
x <-M[,3] y <- M[,4] n <- nrow(M) #按照公式設定分子 Numerator <- (n*sum(x*y)-sum(x)*sum(y)) #按照公式設定分母 Denominator <- (sqrt(n*sum(x^2)-sum(x)^2)*sqrt(n*sum(y^2)-sum(y)^2)) #計算出相關係數r r <- Numerator / Denominator r [1] -0.5884779 T <- r*(sqrt(n-2))/sqrt(1-r^2) T #使用公式cor.text(~x+y,data=M)得到顯著性檢驗輸出結果,對於p<alpha,拒絕原假設,認為兩個隨機變數具有一定的線性關係
顯示統計量t,自由度 df,檢驗p值p-value
2.偏相關係數
偏相關係數是在消除其他變數的影響條件下,計算某兩個變數之間的相關係數,能夠顯示出和相關係數不一樣的相關性性質。
#計算偏相關係數 x<-read.table("",head=ture) cor(x) t.df<-nrow(x)-ncol(x)#自由度n-p ndata<-nrow(x) nvar<-ncol(x) r12=cor(x[1,2]-cor(x)[1,3]*cor(x)[2,3])/aqrt(1-cor(x)[1,3]^2)*sqrt(1-cor(x)[2,3]^2)) t<-r12*sqrt(ndata-nvar)/sqrt(1-r12^2) p1<-pt(t,t.df) p2<-p1-0.5 if(any(p2<=0)) p<-2*p1 else p<-2*(1-p1) data.frame(parial.coefs12=r12,t<-t,df<-t.df,p-value=p)
3.複相關係數
x<-
det(cor(x))
M11<-coor(x)[-1,-1]
det(M11)
r<-sqrt(1-det(cor(x))/det(M11))
F<-(nrow(x)-ncol(x))/(ncol(x)-1)*r^2/(1-r^2)