吳恩達機器學習之多變數線性迴歸實現部分
阿新 • • 發佈:2018-12-06
C++實現梯度下降法
“linear_regression.h”
//多變數線性迴歸模型 struct elem_var2 { double y; double* x; //用陣列傳入自變數資料(x[0]=1,便於之後的計算) }; class var2_lin_reg { public: var2_lin_reg(int xnum, elem_var2* p, int size, double rate); //初始化 ~var2_lin_reg(); //析構 void scaling(); //特徵縮放器(將所有特徵值統一縮放至1--10) void scalback(); //特徵還原(引數縮放) double cost_fuction(); //返回當前預測方程對應代價函式的值 void update(); //同時更新方程引數 void find(); //最小化代價函式,找到收斂點時對應的方程引數 double* get_par(int &par_num); //獲得當前方程的引數 double est_val(double* x); //使用擬合後的迴歸方程進行預測 private: int x_num; //自變數個數 elem_var2* tran_set; //訓練集(讀入時將x【0】賦值為1) int setsize; //訓練集資料量 double* par; //引數陣列(大小為實際x_num+1):h(x)=par0*x0(賦值為1)+par1*x1+par2+x^2+...+par(x_num)*x^x_num double learn_rate; //學習速率 double* x_scal; //特徵縮放率 };
“linear_regression.cpp”
//多變數線性迴歸 var2_lin_reg::var2_lin_reg(int xnum, elem_var2* p, int size, double rate) {//引數列表:自變數數目,訓練集地址,訓練集容量,學習速率 x_num = xnum+1; //設定自變數數目 setsize = size; //獲取訓練集大小 tran_set = p; //指標指向訓練集陣列 learn_rate = rate; //設定學習速率 par = new double[xnum + 1]; //係數初始化為0 memset(par, 0, sizeof(double)*(xnum + 1)); x_scal = new double[xnum + 1]; //特徵縮放率初始化為1 for (int i = 0;i < x_num;i++) x_scal[i] = 1; } var2_lin_reg::~var2_lin_reg() { tran_set = NULL; setsize = 0; delete[]par; par = NULL; delete[]x_scal; x_scal = NULL; } void var2_lin_reg::scaling() {//特徵縮放器 for (int j = 0;j < x_num;j++) {//以第一組資料確定縮放率 while (tran_set[0].x[j] > 10 || tran_set[0].x[j] < 1) { if (tran_set[0].x[j] > 10) { tran_set[0].x[j] /= 10.0; x_scal[j] *= 10.0; } else { tran_set[0].x[j] *= 10.0; x_scal[j] /= 10.0; } } } for (int i = 1;i < setsize;i++) {//對剩餘資料進行縮放 for (int j = 0;j < x_num;j++) { tran_set[i].x[j] /= x_scal[j]; } } } void var2_lin_reg::scalback() {//特徵還原,引數縮放 for (int i = 0;i < x_num;i++) par[i] /= x_scal[i]; } double var2_lin_reg::cost_fuction() { //返回當前預測方程對應代價函式的值 double hx, sum = 0; for (int i = 0;i < setsize;i++) { hx = 0; for (int j = 0;j < x_num;j++) { hx += par[j] * tran_set[i].x[j]; } sum += (hx - tran_set[i].y)*(hx - tran_set[i].y); } return (sum / 2.0 / setsize); } void var2_lin_reg::update() {//同時更新方程引數 double hx; double* sum = new double[x_num]; for (int j = 0;j < x_num;j++) { sum[j] = 0; for (int i = 0;i < setsize;i++) { hx = 0; for (int t = 0;t < x_num;t++) { hx += par[t] * tran_set[i].x[t]; } sum[j] += (hx - tran_set[i].y)*tran_set[i].x[j]; } } for (int i = 0;i < x_num;i++) par[i] -= learn_rate * sum[i] / (double)setsize; delete[]sum; } void var2_lin_reg::find() {//最小化代價函式,找到收斂點時對應的方程引數 scaling(); //資料放縮 double cost_pre, cost_last; cost_pre = cost_fuction(); update(); //更新引數 cost_last = cost_fuction(); while (cost_pre != cost_last) {//尋找收斂點 /* cout << cost_pre << " " << cost_last << endl; //用來選擇學習率 */ cost_pre = cost_last; update(); cost_last = cost_fuction(); } //獲得假設函式最優擬合時的引數 scalback(); //特徵還原,引數縮放 } double* var2_lin_reg::get_par(int &par_num) {//獲得當前方程的引數 par_num = x_num; return par; } double var2_lin_reg::est_val(double* x) {//使用擬合後的迴歸方程進行預測 double hx = 0; for (int i = 0;i < x_num;i++) { hx += par[i] * x[i]; } return hx; }
主函式部分:
int main() {//多變數線性迴歸測試 int size, xnum; cout << "請輸入訓練集容量:"; cin >> size; cout << "請輸入變數個數: "; cin >> xnum; elem_var2 transet[200]; for (int i = 0;i < size;i++) { transet[i].y = 0; transet[i].x = new double[xnum + 1]; memset(transet[i].x, 0, sizeof(double)*(xnum + 1)); } cout << "請輸入訓練集資料:" << endl; for (int i = 0;i < size;i++) { transet[i].x[0] = 1; for (int j = 1;j <= xnum;j++) cin >> transet[i].x[j]; cin >> transet[i].y; } var2_lin_reg obj(xnum, transet, size, 0.042); obj.find(); double*par = NULL; int parnum; par=obj.get_par(parnum); cout << "h(x)=" << par[0]; for (int i = 1;i < parnum;i++) { if (par[i] > 0) cout << '+' << par[i] << "*x" << i; else { if (par[i] < 0) cout << par[i] << "*x" << i; } } cout << endl; /* double*x = new double[xnum + 1]; memset(x, 0, sizeof(double)*(xnum + 1)); double flag; while (cin >> flag) {//預測部分 if (flag == 0) break; x[0] = 1; for (int i = 1;i <= xnum;i++) cin >> x[i]; flag = obj.est_val(x); cout << flag << endl; } delete[]x; */ for (int i = 0;i < size;i++) { delete[]transet[i].x; } return 0; }
關於一些操作細節:
以吳恩達老師的訓練集為例。
1.學習率選擇:
find函式中有一行用於選擇學習率的程式碼:
cout << cost_pre << " " << cost_last << endl;
下面來實際操作一下:
主函式學習率設為:0.042是通過測試得出的。
如果將學習率設定較大,輸出的代價函式值結果如下:
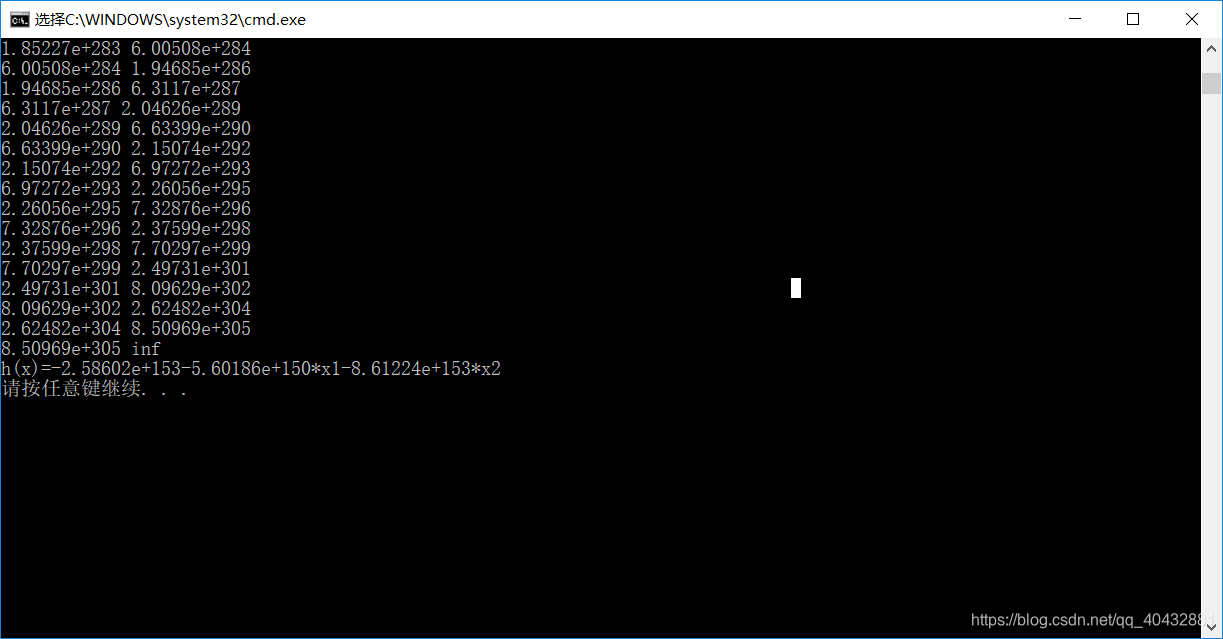
所以,可將學習率適當減小,通過不斷測試得出一下結果:
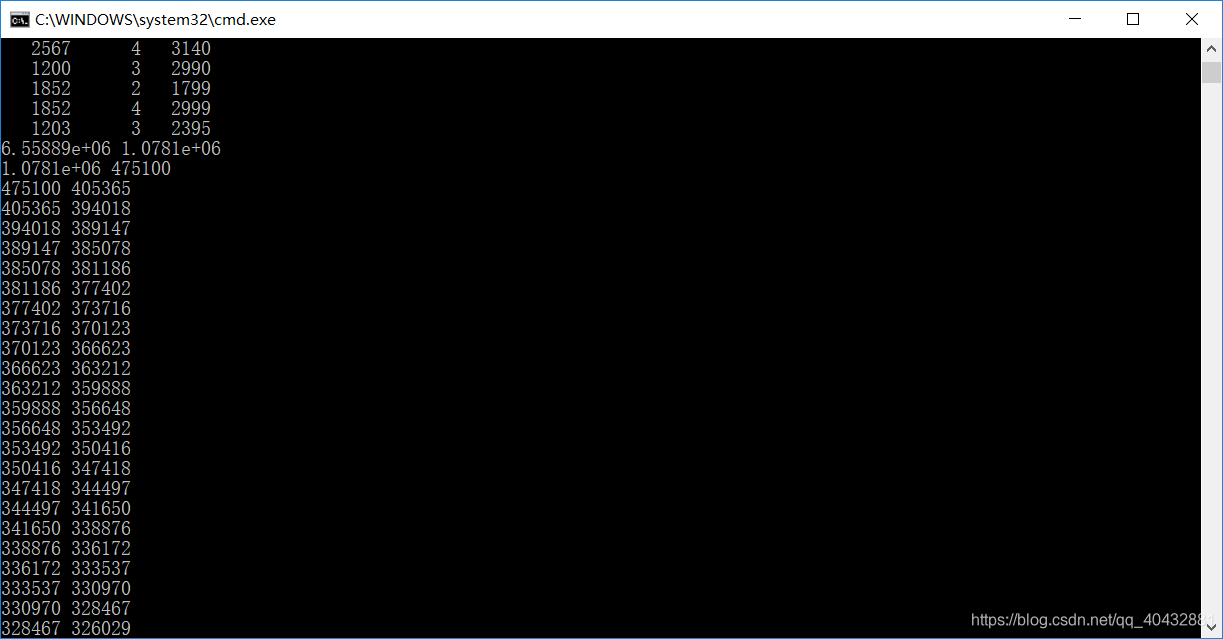
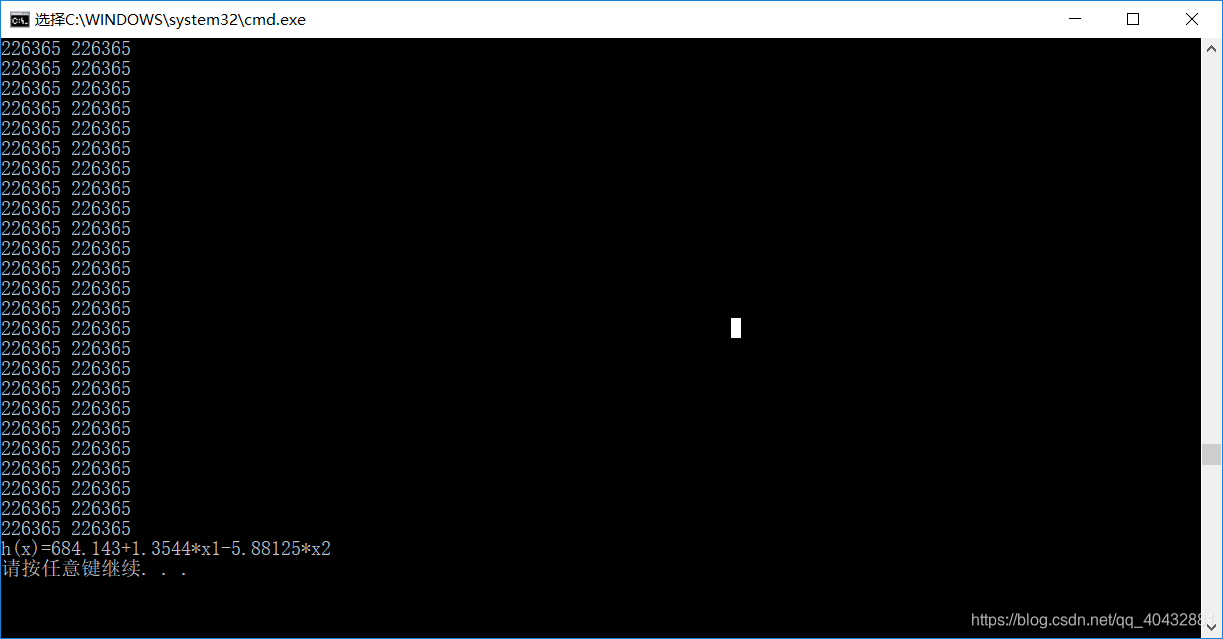
2.特徵縮放:將所有特徵縮放至【1–10】
特徵縮放和特徵還原:
void scaling(); //特徵縮放器(將所有特徵值統一縮放至1–10)
void scalback(); //特徵還原(引數縮放)
在find函式中先進行特徵縮放,將資料集內的特徵值縮放,最後得出的對應引數便放縮(反向),之後再進行特徵還原(例如特徵值縮小,最後得出的引數便增大,需要將對應引數再進行縮小(縮小比例與特徵值縮小比例一致))
Octave實現正規方程法
>> A=load('space(x1)_bedroom(x2).txt');
>> B=load('price(y).txt');
>> t=ones(47,1);
>> X=[t A];
>>Y=B;
>>par=pinv(X'*X)*X'*Y
par =
684.1446
1.3544
-5.8816
獲得的引數向量與上面的梯度下降法得出的結果近似。
